Conteúdos

Este roteiro de estudos de matemática apresenta o conceito de função afim, também conhecida como função do 1º grau. Inicia com uma breve discussão sobre a função afim, e a apresentação de sua lei de formação, identificando cada um de seus termos. Nas etapas posteriores, traz sugestões de textos e vídeos, para maior aprofundamento acerca de tal tipo de função, bem como de seu comportamento, que pode ser crescente ou decrescente. Na penúltima etapa, trata de outro tipo de função específica: a função constante. Ao final, há alguns exercícios resolvidos.

● Introdução ao tema;
● Função afim;
● Função afim crescente e decrescente;
● Função constante; e
● Cheque seus conhecimentos.

Objetivos

● Aprender o que é uma função afim;
● Aprender a identificar os coeficientes angular e linear de uma função afim; e
● Compreender a representação gráfica de uma função afim.

Estude também:

Estudar em casa: função composta

Estudar em casa: fatorial de um número natural

Palavras-chave:

Função afim. Função crescente. Função decrescente. Função constante.

Proposta de trabalho:

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: Introdução ao tema

O estudo dos mais diversos tipos de funções, bem como a análise dos seus comportamentos, consiste numa área fundamental da Matemática. Dentre os diversos tipos de funções que existem, destacamos a função do primeiro grau, também conhecida como função afim.
A função afim (função do primeiro grau) é um caso particular de um grupo de funções mais geral: a função polinomial. Uma função polinomial de grau um é também chamada de função do primeiro grau (a função afim).
A estrutura matemática genérica (lei de formação) de toda e qualquer função do primeiro grau é a seguinte:

f(x)=ax+b

Identificando cada um dos termos da função afim, temos:

a →coeficiente angular (o termo que acompanha a incógnita);
x →incógnita,cujo grau (expoente) é um (1) ;
b →coeficiente linear (o termo que não está acompanhado da incógnita) .

Uma função afim pode ser crescente ou decrescente, e quem determina tal comportamento é justamente o sinal (positivo {+} ou negativo {−}) que acompanha o seu coeficiente angular (a).

Dessa forma:
Para o caso de uma função afim com o coeficiente angular positivo, ou seja, a > 0, temos uma função afim crescente. Exemplo:

f(x)=5x+13

Para o caso de uma função afim com o coeficiente angular negativo, ou seja, a < 0, temos uma função afim decrescente. Exemplo:

f(x)=-17x+30

Para o caso em que o coeficiente angular é nulo, ou seja, a = 0, obtemos uma função constante. Exemplo:

f(x)=27

Este roteiro de estudos consiste em uma sugestão de caminho a ser trilhado por você, leitor(a) estudante, para uma maior e melhor compreensão dos conteúdos apresentados nesta seção. Bons estudos!

2ª Etapa: Função afim

Pergunta norteadora: O que é uma função afim?

GOUVEIA, Rosimar. “Função Afim”; Toda Matéria
Acesso em: 15 de outubro de 2022.

A partir da leitura da introdução deste material, bem como do texto acima, responda às seguintes perguntas:

1- Complete: A função afim é também conhecida como…
2- Como é chamado o termo que acompanha a incógnita, em uma função afim?
3- Como é chamado o termo que não é acompanhado pela incógnita, em uma função afim?
4- Complete: Uma função que possui coeficiente angular nulo (a = 0), ou seja, que possui apenas coeficiente linear, é uma função…
5- Como é o gráfico de uma função afim?
6- Qual é o significado geométrico do coeficiente angular (a)?

Respostas das perguntas da 2ª etapa:

1- A função afim é também conhecida como função do primeiro (1º) grau.

2- O termo que acompanha a incógnita é o coeficiente angular (a).

3- O termo que não é acompanhado pela incógnita é o coeficiente linear (b).

4- Uma função que possui coeficiente angular nulo (a = 0) é uma função constante, possui apenas coeficiente linear (b).

5- O gráfico de uma função do primeiro (1º) grau, ou seja, de uma função afim, é uma reta oblíqua aos eixos das abcissas e das ordenadas.

6- O coeficiente angular em uma função afim representa a inclinação da reta em relação ao eixo das abscissas (O_x).

Para saber mais, assista:

Função Afim 01: O que é função afim? – Matemática no papel
Acesso em: 15 de outubro de 2022.

Função do 1º Grau: Definição e Gráfico – Equaciona com Paulo Pereira
Acesso em: 15 de outubro de 2022.

3ª Etapa: Função afim crescente e decrescente

Pergunta norteadora: Como determinar se uma função afim cresce ou decresce?

NOÉ, Marcos. “Função crescente e função decrescente”; Brasil Escola
Acesso em: 15 de outubro de 2022.

A partir da leitura do texto acima, responda às seguintes perguntas:

1- Qual é o termo que determina o crescimento, ou o decrescimento, de uma função do 1º grau?
2- A qual conjunto numérico pertencem os coeficientes angular (a) e linear (b) de uma função do 1º grau?
3- Analise as funções a seguir, identifique cada um dos seus termos e as caracterize como função crescente ou função decrescente:
a) f(x)=x-4
b) f(x)=- x+100
c) f(x)=3x+10
d) f(x)=-300x+70

Respostas das perguntas da 3ª etapa:

É o coeficiente angular (a).

O coeficiente angular (a) e o coeficiente linear (b) pertencem ao conjunto dos números reais (ℝ), com a≠0.

f(x)=x-4
Coeficiente angular → a = 1 > 0 (positivo), portanto, função crescente
Coeficiente linear → b = − 4

f(x)=- x+100
Coeficiente angular → a = − 1 < 0 (negativo), portanto, função decrescente
Coeficiente linear → b = 100

f(x)=3x+10
Coeficiente angular → a = 3 > 0 (positivo), portanto, função crescente
Coeficiente linear → b = 10

d) f(x)=-300x+70
Coeficiente angular → a = − 300 < 0 (negativo), portanto, função decrescente
Coeficiente linear → b = 70

Para saber mais, assista:

Função crescente e decrescente – Brasil Escola
Acesso em: 15 de outubro de 2022.

4ª Etapa: Função constante

Pergunta norteadora:

O que caracteriza uma função constante?
RIBEIRO, Amanda Gonçalves. “Função constante”; Mundo Educação.
Acesso em: 15 de outubro de 2022.

A partir da leitura do texto acima, responda às seguintes perguntas:

1- Qual é a lei de formação de uma função constante?
2- O que diferencia uma função afim de uma função constante?
3 – Como é o gráfico de uma função constante?

Respostas das perguntas da 4ª etapa:

A lei de formação de uma função constante é:
f(x)=c

A função afim é caracterizada pelo grau um de sua incógnita, que é sempre acompanhada por um coeficiente angular diferente de zero (a≠0). A função constante, por sua vez, não possui incógnita, ou seja, possui coeficiente angular nulo (a=0).

O gráfico de toda e qualquer função constante será sempre uma reta paralela ao eixo das abscissas, ou seja, ao eixo O_x.

Para saber mais, assista:

Função 12: Função Constante – Matemática no papel
Acesso em: 15 de outubro de 2022.

5ª Etapa: Cheque seus conhecimentos

Realizar questões de vestibular e do ENEM é um excelente exercício durante o estudo autodirigido. Isso porque essas questões são seguidas de gabarito, mesmo quando são dissertativas. Abaixo, alguns exemplos de questões sobre o tema estudado:

1- Classifique cada uma das funções seguintes em crescente ou decrescente:
a) y = 4x + 6
b) f(x) = – x + 10
c) y = (x + 2)² – (x – 1)²

Resolução:
Em uma função do tipo y = ax + b, o coeficiente a de x indica se a função é crescente ou decrescente.
a) y = 4x + 6

Nessa função, a = 4 > 0, portanto, y é uma função crescente.

b) f(x) = – x + 10

Como a = – 1 < 0, f(x) é uma função decrescente. C) y = (x + 2)² – (x – 1)² Nesse caso precisamos desenvolver os parênteses através dos produtos notáveis.

Como a = 6 > 0, y é uma função crescente.

Disponível em: Mundo Educação.
Acesso em: 15 de outubro de 2022.

2- (UFPI) A função real de variável real, definida por f (x) = (3 – 2a)x + 2, é crescente quando:
a) a > 0
b) a < 3/2 c) a = 3/2 d) a > 3/2
e) a < 3 Resposta: B. Resolução: Para que a função seja crescente, é necessário que o coeficiente de x seja positivo, logo:

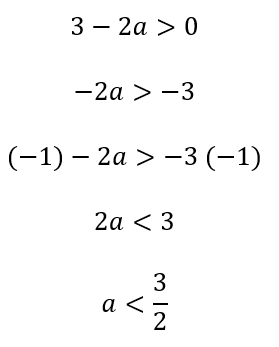
Portanto, a alternativa correta é a letra b.

Disponível em: Mundo Educação.
Acesso em: 15 de outubro de 2022.

(UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:
A) 5 km
B) 10 km
C) 15 km
D) 20 km
E) 25 km

Resposta: C.

Resolução:
Seja d a distância percorrida em quilômetros, sabemos que:
19=0,96d+4,6
Isolando a incógnita, temos que:

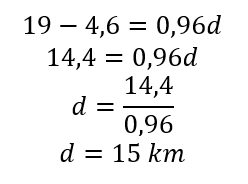
Disponível em: Brasil Escola.
Acesso em: 15 de outubro de 2022.

4- Podemos afirmar que o zero da função f(x) = -2x + 5 é igual a:
A) 2
B) 2,5
C) -2,5
D) -3
E) 3

Resposta: B.

Resolução:
Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então, temos que:

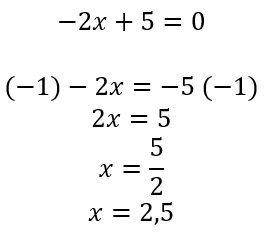
Disponível em: Brasil Escola.
Acesso em: 15 de outubro de 2022.

Roteiro de estudos elaborado pelo Prof. Me. Elves Silva Moreira.
Revisão textual: Professora Daniela Leite Nunes.
Coordenação Pedagógica: Prof.ª Dr.ª Aline Monge