Conteúdos

Este roteiro de estudos de matemática apresenta, de forma introdutória, um tipo particular de função: a função composta. Inicia-se com uma sugestão de leitura, seguida por perguntas sobre o texto sugerido. A segunda etapa consiste na apresentação de alguns exemplos resolvidos, e por fim, na terceira etapa, há exercícios resolvidos de vestibulares, para uma maior consolidação do conteúdo. O material também conta com sugestões de vídeo e textos, possibilitando a ampliação e o aprofundamento em determinados tópicos.

● Função composta; e
● Alguns exemplos resolvidos.

Objetivos

● Compreender o que é uma função composta;
● Compreender o que é o domínio e o contradomínio de uma função; e
● Aprender a operar algebricamente com funções compostas.

Palavras-chave:

Tipos de funções. Função composta. Domínio da função. Contradomínio da função.

Proposta de trabalho:

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar a sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: Função composta

Pergunta norteadora: O que é uma função composta?

Função Composta – Brasil Escola – Luiz Paulo Moreira
SILVA, Luiz Paulo Moreira. “Função Composta”; Brasil Escola.
Acesso em: 04 de fevereiro de 2022.

A partir da leitura do texto acima, responda às seguintes perguntas:

1 – O que é uma função?
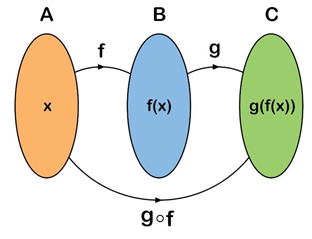
2 – Considere uma função f e uma outra função g. Como podemos definir a função composta de g com f [gof = g(f(x))]?
3 – Como a função composta relaciona os elementos das funções?
4 – Analise o diagrama a seguir, que mostra o comportamento das funções f, g e h, e responda às perguntas:

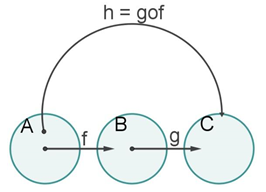
a) Qual função relaciona os elementos do conjunto A com os elementos do conjunto B?
b) Qual função relaciona os elementos do conjunto B com os elementos do conjunto C?
c) Qual função relaciona os elementos do conjunto A diretamente com os elementos do conjunto C?
d) Qual conjunto representa o domínio da função f?
e) Qual conjunto representa o contradomínio (imagem) da função f?
f) Qual conjunto representa o domínio da função g?
g) Qual conjunto representa o contradomínio (imagem) da função g?
h) Qual conjunto representa o domínio da função h?
j) Qual conjunto representa o contradomínio (imagem) da função h?

Para saber mais, leia e assista:

Função Composta – InfoEscola – José Roberto Lessa
Acesso em: 04 de fevereiro de 2022.

Função 10: Composta – Equaciona Com Paulo Pereira
Acesso em: 04 de fevereiro de 2022.

Gabarito da 2ª Etapa:

1 – Função é uma regra que relaciona cada elemento de um conjunto, chamado domínio, a um único elemento de um outro conjunto, chamado de contradomínio.

2 – A função composta de g com f, que também pode ser escrita como gof, ou g(f(x)), é uma regra que relaciona cada elemento do domínio da função f a um único elemento do contradomínio da função g.

3 – A função composta relaciona os elementos do domínio de uma função a elementos do contradomínio de outra função.

4 –
a) A função f.
b) A função g.
c) A função h, que é a função composta de g com f, a qual pode ser representada como:
h=gof=g(f(x))
d) O domínio da função f é o conjunto A.
e) O contradomínio (imagem) da função f é o conjunto B.
f) O domínio da função g é o conjunto B.
g) O contradomínio (imagem) da função g é o conjunto C.
h) O domínio da função h é o conjunto A.
j) O contradomínio (imagem) da função h é o conjunto C.

2ª Etapa: Alguns exemplos resolvidos

Nesta etapa, veremos alguns exemplos resolvidos, para uma melhor compreensão de como trabalhar algebricamente com a função composta.

Exemplo 1 – Considere as funções

Calcule:
a) gof
b) fog

Resolução:
a) Primeiramente, podemos reescrever a função composta da seguinte maneira:

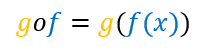
Agora, vamos substituir a função

Neste momento, vamos aplicar o que está entre parênteses (na cor azul) na função g, ou seja:

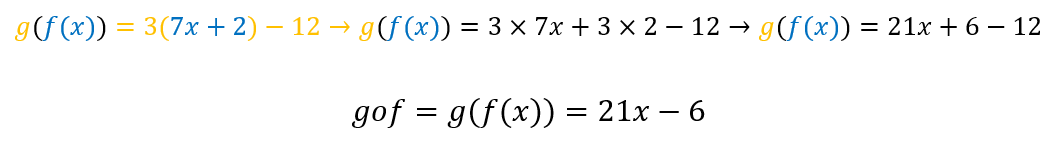
b) Novamente, começamos reescrevendo a função composta:

E agora, vamos aplicar o que está entre parênteses (na cor laranja) na função f, da seguinte maneira:

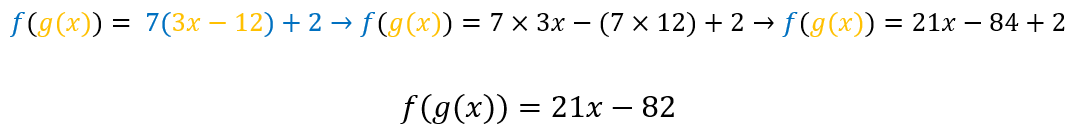
Pela resolução da letra (a) e da letra (b), do exemplo 1, percebe-se que:

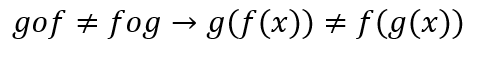
Vejamos mais um exemplo:
Exemplo 2 – Considere as funções

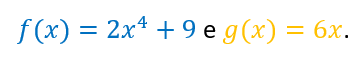
Calcule:
a) gof
b) fog

Resolução:
a) Vamos reescrever a função composta:

Aplicando o que está entre parênteses (na cor azul) na função g, temos:

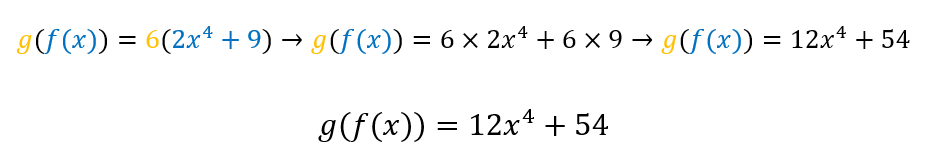
b) Reescrevendo a função composta:

Novamente, constatamos que:

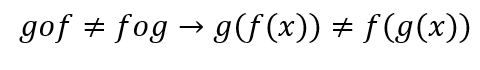
3ª Etapa: Cheque seus conhecimentos

Realizar questões é um excelente exercício durante o estudo autodirigido. Abaixo, alguns exemplos de questões sobre o tema estudado:

1) Dada as funções de lei de formação f(x) = 2x + 5 e g(x) = -3x + 1, podemos afirmar que o valor de f (g(1)) é igual a:
A) 0
B) 1
C) 2
D) 3
E) 4

Resposta: B

Resolução:
Primeiro calcularemos g(1):
g(x)=-3x+1
g(1)=-3×1+1
g(1)=-3+1
g(1)=-2

Agora que conhecemos o valor de g(1), calcularemos f(g(1)), ou seja, f(-2):
f(x)=2x+5

f(-2)=2(-2)+5

f(-2)=-4+5

f(-2)=1

Disponível em: Brasil Escola.
Acesso em: 04 de fevereiro de 2022.

2) Dada a função f(x) = x + 3 e a função g(x) = 2x – 5, o zero da função f(g(x)) é:
A) 0
B) 1
C) 2
D) -1
E) -2

Resposta: B

Resolução:
Primeiro encontraremos f(g(x)):
f(g(x))=(2x-5)+3
f(g(x))=2x-5+3
f(g(x))=2x-2

Para encontrar o zero da função, vamos igualar a função a zero, ou seja:
2x-2=0
2x=2
x=2/2
x=1

Disponível em: Brasil Escola.
Acesso em: 04 de fevereiro de 2022.

3) (Mackenzie – SP) As funções f(x) = 3 – 4x e g(x) = 3x + m são tais que f(g(x)) = g(f(x)), qualquer que seja x real. O valor de m é:

a) 9/4
b) 5/4
c) -6/5
d) 9/5
e) -2/3

Resposta: C

Resolução:
Primeiro encontraremos f(g(x)):
f(g(x))=f(3x+m)=3-4x
f(g(x))=3-4(3x+m)
f(g(x))=3-12x-4m
f(g(x))=-12x-4m+3

Agora encontraremos g(f(x)):
g(f(x))=g(3-4x)
g(f(x))=3(3-4x)+m
g(f(x))=9-12x+m
g(f(x))=-12x+m+9

Por fim, vamos igualar as duas leis de formação:
-12x+m+9=-12x-4m+3
-12x+12x+4m+m=3-9
5m=-6
m=-6/5

Disponível em: Brasil Escola.
Acesso em: 04 de fevereiro de 2022.

4) (Acafe – SC) Dadas as funções reais f(x) = 2x – 6 e g(x) = ax + b, se f[g(x)] = 12x + 8, o valor de a + b é:
A) 10
B) 13
C) 12
D) 20

Resposta: B

Sendo
f(x)=2x-6; g(x)=ax+b e f(g(x))=12x+8,

então, temos que:
f(g(x))=f(ax+b)=2(ax+b)-6
f(g(x))=2ax+2b-6

Como f(g(x))=12x+8, temos:
12x+8=2ax+2b-6

Igualando os termos para encontrar o valor de a, temos que:
2ax=12x
2a=12
a=12/2
a=6

Encontrando o valor de b:
2b-6=8
2b=8+6
2b=14
b=14/2
b=7
Por fim, o valor de a + b:
6+7=13

Disponível em: Brasil Escola.
Acesso em: 04 de fevereiro de 2022.

Roteiro de estudos elaborado pelo Professor Elves Silva Moreira
Coordenação Pedagógica: Dr.ª Aline Bitencourt Monge