Conteúdos

Este roteiro de estudos de matemática apresenta, de forma introdutória, os métodos de resolução de situações-problema que envolvem grandezas diretamente, ou inversamente, proporcionais: a regra de três simples e a regra de três composta. O material também conta com algumas sugestões de textos e vídeos (possibilitando uma ampliação da abordagem e o aprofundamento em determinados tópicos). Ao final, há diversos exercícios resolvidos.

● Regra de três simples;
● Regra de três composta; e
● Exercícios.

Objetivos

● Aprender a utilizar a regra de três simples;
● Aprender a utilizar a regra de três composta; e
● Aprender a diferenciar quando uma grandeza é diretamente ou inversamente proporcional a uma outra grandeza.

Estude também:

Estudar em casa: matrizes inversas e transpostas

Estudar em casa: números complexos

Palavras-chave:

Regra de três simples. Regra de três composta. Grandeza diretamente proporcional. Grandeza inversamente proporcional.

Proposta de trabalho:

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há exercícios resolvidos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: Introdução

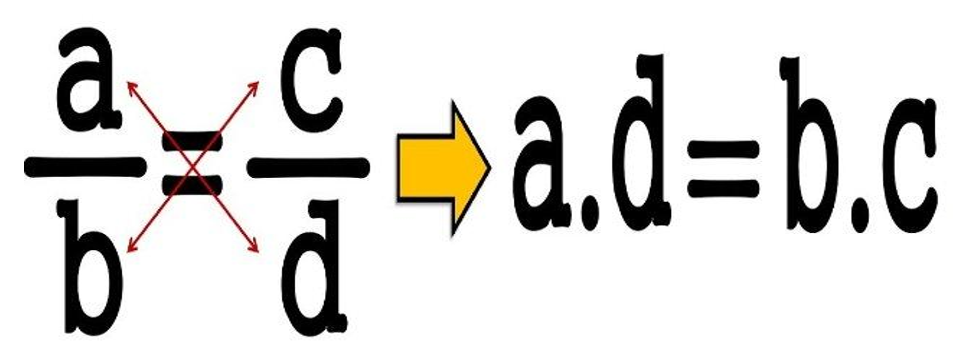
Nas mais diversas disciplinas¹, tais como: Física, Química e Matemática, não é incomum nos depararmos com situações-problema que envolvam duas ou mais grandezas proporcionais, em que precisamos determinar a relação correta entre elas para, a partir dos dados fornecidos pelo problema, encontrarmos o valor de uma determinada incógnita (x).

Contudo, para proceder de forma correta e segura, é preciso fazer uma análise criteriosa a respeito da natureza da proporcionalidade entre as grandezas envolvidas na situação-problema. Ou seja, precisamos identificar se as grandezas são diretamente proporcionais (isso se dá nos casos em que elas exibem o mesmo comportamento: quando uma aumenta, a outra também aumenta e/ou quando uma diminui, a outra também diminui), ou se trata-se de grandezas inversamente proporcionais (apresentam comportamento oposto: quando uma diminui, a outra aumenta e/ou quando uma aumenta, a outra diminui).

Saber identificar a natureza da proporcionalidade (direta ou inversa) é a chave para utilizar de forma adequada os métodos de resolução de problemas, por meio da regra de três simples e da regra de três composta.
Este roteiro de estudos pretende guiar o(a) leitor(a) neste caminho.

Bons estudos!

¹ Bem como no dia a dia, seja em um supermercado fazendo compras, seja num posto de gasolina abastecendo um automóvel, etc.

2ª Etapa: Regra de três simples

Pergunta norteadora: O que é a regra de três simples?

OLIVEIRA, Raul Rodrigues de. “Regra de três simples”. Brasil Escola
Acesso em 23 de outubro de 2021.

A partir da leitura do texto acima, responda às seguintes perguntas:

1- Como podemos identificar uma grandeza diretamente proporcional à outra grandeza?
2- Como podemos identificar uma grandeza inversamente proporcional à outra grandeza?
3- Em quais situações-problema podemos aplicar o método da regra de três simples?
4- Cite um exemplo que envolva duas grandezas diretamente proporcionais.
5- Cite um exemplo que envolva duas grandezas inversamente proporcionais.
6- Como aplicar, de forma correta, a regra de três simples?

Respostas das perguntas da 2ª Etapa:

1- À medida em que uma grandeza aumenta, a outra grandeza aumenta na mesma proporção.

2- À medida em que uma grandeza diminui, a outra grandeza aumenta na mesma proporção.

3- Ela pode ser utilizada sempre que, numa dada situação-problema, houver 2 grandezas proporcionais. Para cada uma das grandezas, atribui-se dois valores, sendo que três dos quatro valores são conhecidos (dados do problema).

4- Preço e peso de um determinado produto (por exemplo, frutas). Quanto maior o peso, maior será o preço.

5- Velocidade de um carro e tempo de viagem. Quanto maior a velocidade de um carro, menor o tempo que ele irá gastar para percorrer uma determinada distância (tempo de viagem).

6- É possível seguir os seguintes passos:
1º -> Identificar as grandezas e construir uma tabela, organizando as informações dadas pelo problema;
2º -> Analisar se as grandezas são diretamente ou inversamente proporcionais; e
3º -> Aplicar o método adequado de resolução da situação-problema e, assim, resolver a equação resultante.

Para saber mais, assista:
Regra de três simples – Professora Angela Matemática
Acesso em 23 de outubro de 2021.

3ª Etapa: Regra de três composta

Pergunta norteadora: O que é a regra de três composta?

Regra de três composta – Toda Matéria
Acesso em 23 de outubro de 2021.

A partir da leitura do texto acima, responda às seguintes perguntas:

1- Em quais situações-problema podemos aplicar o método da regra de três composta?
2- A partir de quantas grandezas deve-se utilizar a regra de três composta?
3- Como aplicar, de forma correta, a regra de três composta?

Respostas das perguntas da 3ª Etapa:

1- Nas situações problemas que envolvam grandezas diretamente proporcionais, ou inversamente proporcionais.

2- Acima de duas grandezas proporcionais, ou seja, com três, quatro, ou mais grandezas, direta ou inversamente proporcionais.

3- Pode-se seguir os seguintes passos:
1º -> Verificar quais são as grandezas envolvidas na situação-problema e, assim, construir uma tabela com os dados fornecidos;
2º -> Determinar o tipo de relação que existe entre as grandezas envolvidas, ou seja, se são grandezas diretamente proporcionais, ou se são grandezas inversamente proporcionais; e
3º -> Efetuar os cálculos utilizando os dados fornecidos pela situação-problema.

Para saber mais, assista:
Regra de três composta – Professora Angela Matemática
Acesso em 23 de outubro de 2021.

4ª Etapa: Cheque seus conhecimentos

Realizar questões é um excelente exercício durante o estudo autodirigido. Abaixo, alguns exemplos de questões sobre o tema estudado:

1) Para atender a alta demanda em smartphones, uma fábrica decidiu aumentar o número de produtos produzidos diariamente. Para isso, ela investiu em mais 3 máquinas, totalizando-se 8 máquinas. Sabendo-se que eram produzidos diariamente 750 smartphones, haverá um aumento na produção diária de:

A) 1200
B) 1000
C) 210
D) 350
E) 450

Resposta: E

Resolução:
Analisando as grandezas, estamos trabalhando com quantidade de máquinas e quantidade de smartphones. Além disso, sabemos que se eu aumento o número de máquinas, a minha produção também aumentará, logo, as grandezas são diretamente proporcionais, assim, multiplicaremos cruzado.
Note que havia um total de 8 máquinas quando foram adquiridas mais 3, então, como o nosso interesse é saber somente quanto a mais a fábrica vai produzir, e sabendo que:

8-3=5

A tabela ficará da seguinte maneira:

Disponível em: Brasil Escola.
Acesso em: 23 de outubro de 2021.

2) A chuva, quando em excesso, traz vários problemas para a população. Em uma determinada cidade brasileira, houve a danificação da estrutura de uma ponte. Para arrumá-la, a prefeitura constatou que seriam necessários 12 funcionários para terminar a obra em 2 meses. Sabendo que era ano político e visando à reeleição, o prefeito decidiu que terminaria a obra em 15 dias. A quantidade de funcionários necessários para realizar a obra nesse período é de:

A) 18
B) 24
C) 36
D) 48
E) 52

Resposta: D

Resolução:
As grandezas são tempo e quantidade de funcionários, e, analisando a situação sabemos que, para diminuir o tempo, a quantidade de funcionários precisa aumentar, logo, essas grandezas são inversamente proporcionais. Quando isso ocorre, construímos a tabela e multiplicamos reto (e não de forma cruzada). Como um tempo foi dado em dias, e o outro, em meses, utilizaremos 60 dias para representar os 2 meses.

Disponível em: Brasil Escola.
Acesso em: 23 de outubro de 2021.

3) Durante o ano de 2020, devido à pandemia de COVID-19, o mundo viu-se dependente da criação de uma vacina para imunizar a população. No Brasil não foi diferente, e a corrida por uma vacina eficaz só terminou no ano de 2021. A primeira delas foi a Coronavac, produzida pelo Instituto Butantan, que anunciou que a vacina possui 78% de eficácia em casos leves. Isso significa que, se 100 pessoas forem vacinadas, 78 pessoas não terão sintoma algum e 22 pessoas terão sintomas leves.
A partir desse anúncio, iniciou-se a campanha de imunização. Supondo-se que a cidade de Abadia de Goiás (próxima da capital Goiânia) tenha conseguido vacinar toda a sua população, que é de 8 950 habitantes, e considerando-se que toda ela tenha contato com o vírus e que essa proporção seja mantida, a quantidade de pessoas que terão sintomas leves nessa população será de:

A) 6979
B) 6780
C) 2170
D) 1969
E) 1852

Resposta: D

Resolução:
Analisando a situação, as grandezas são: pessoas vacinadas (PV) e pessoas com sintomas leves (PL). Com essas grandezas, o primeiro passo será montar a tabela.

Sabemos que 100 está para 22 assim como 8950 está para x, em que x é a quantidade de pessoas que terão sintomas leves nessa população.

Agora, analisando a proporcionalidade entre essas grandezas, se se aumenta o número de pessoas vacinadas, é possível concluir que a quantidade de pessoas que apresentam sintomas leves também será maior, logo, estamos trabalhando com grandezas diretamente proporcionais. Quando isso ocorre, basta multiplicar cruzado:

Disponível em: Brasil Escola.
Acesso em: 23 de outubro de 2021.

4) (Unifor) Um texto ocupa 6 páginas de 45 linhas cada uma, com 80 letras (ou espaços) em cada linha. Para torná-lo mais legível, diminui-se para 30 o número de linhas por página e para 40 o número de letras (ou espaços) por linha. Considerando as novas condições, determine o número de páginas ocupadas.
Resolução:

O primeiro passo para responder à questão é verificar a proporcionalidade entre as grandezas.

● A e C são inversamente proporcionais: quanto menos linhas em uma página, maior o número de páginas para ocupar todo o texto.
● B e C são inversamente proporcionais: quanto menos letras em uma página, maior o número de páginas para ocupar todo o texto.
Utilizando setas, a relação entre as grandezas é:

Para encontrar o valor de X devemos inverter as razões de A e B, já que essas grandezas são inversamente proporcionais,

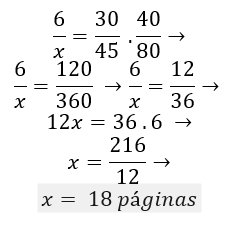
Disponível em: Toda Matéria.
Acesso em: 23 de outubro de 2021.

5) (Vunesp) Dez funcionários de uma repartição trabalham 8 horas por dia, durante 27 dias, para atender certo número de pessoas. Se um funcionário doente foi afastado por tempo indeterminado e outro se aposentou, o total de dias que os funcionários restantes levarão para atender o mesmo número de pessoas, trabalhando uma hora a mais por dia, no mesmo ritmo de trabalho, será
a) 29
b) 30
c) 33
d) 28
e) 31

Resposta: B

Resolução:
O primeiro passo para responder a questão, é verificar a proporcionalidade entre as grandezas.

● A e C são grandezas inversamente proporcionais: menos funcionários levarão mais dias para atender todas as pessoas.
● B e C são grandezas inversamente proporcionais: mais horas trabalhadas por dia farão com que em menos dias todas as pessoas sejam atendidas.
Utilizando setas, a relação entre as grandezas é:

Como as grandezas A e B são inversamente proporcionais a C, para encontrar o valor de x, devemos inverter suas razões.

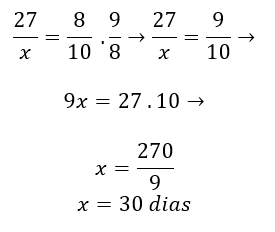
Assim, em 30 dias serão atendidos o mesmo número de pessoas.

Disponível em: Toda Matéria.
Acesso em: 23 de outubro de 2021.

6) (Enem) Uma indústria tem um reservatório de água com capacidade para 900 m3. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m3, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser igual a
a) 2
b) 4
c) 5
d) 8
e) 9

Resposta: C

Resolução:
O primeiro passo para responder à questão, é verificar a proporcionalidade entre as grandezas.

● A e C são grandezas diretamente proporcionais: se a capacidade do reservatório é menor, menos ralos poderão realizar o escoamento.
● B e C são grandezas inversamente proporcionais: sendo menor o tempo para escoamento, maior deverá ser a quantidade de ralos.
Utilizando setas, a relação entre as grandezas é:

Como a grandeza A é diretamente proporcional, sua razão é mantida. Já a grandeza B tem sua razão invertida por ser inversamente proporcional à C.

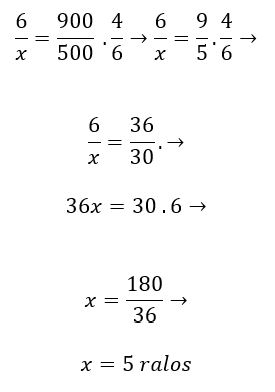
Assim, a quantidade de ralos do novo reservatório deverá ser igual a 5.

Disponível em: Toda Matéria.
Acesso em: 23 de outubro de 2021.

Roteiro de estudos elaborado pelo Professor Elves Silva Moreira
Coordenação Pedagógica: Prof.ª Dr.ª Aline Monge