Conteúdos

Este roteiro de estudos de matemática apresenta, de forma introdutória, o conjunto dos números complexos (C). O material começa com uma breve exposição sobre a representação algébrica dos números complexos e, logo em seguida, com o auxílio de alguns exemplos, apresenta a forma como se deve efetuar operações matemáticas básicas — soma e subtração — entre tais números. O roteiro também conta com algumas sugestões de vídeos e textos, possibilitando uma ampliação e aprofundamento em determinados tópicos, e exercícios resolvidos.

● O que é um número complexo?
● Soma de números complexos; e
● Subtração de números complexos.

Objetivos

● Compreender o que são os números complexos;
● Compreender como se representa um número complexo na forma algébrica; e
● Aprender a efetuar a soma e a subtração de números complexos.

Estude também:

Estudar em casa: entenda os conjuntos numéricos

Estudar em casa: polinômios e seus componentes

Palavras-chave:

Números complexos. Representação algébrica. Parte real. Parte imaginária. Soma. Subtração.

Proposta de trabalho:

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação integral do conteúdo, bem como de seus principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: O que são os números complexos?

Representação algébrica de um número complexo:

Onde

z= número complexo;
a=parte real de z;
b= parte imaginária de z;
i=unidade imaginária.

Pergunta norteadora:

1) O que são os números complexos?

Números Complexos – Educa Mais Brasil – Alana Caiusca
Acesso em 25 de julho de 2021.

A partir da leitura do texto acima, responda às seguintes perguntas:

1- Quais são as partes que formam um número complexo?
2- Quais conjuntos numéricos estão contidos nos números complexos?
3- A raiz quadrada de um número negativo faz parte de qual conjunto numérico?
4- Como representar um número complexo na forma algébrica?
5- O que representa a unidade imaginária na representação algébrica de um número complexo?

Para saber mais, leia e assista:

Números complexos – Brasil Escola
Acesso em 5 de agosto de 2021.

O que é um número complexo? – Toda a Matemática
Acesso em 5 de agosto de 2021.

Gabarito da 1ª etapa:

1- Um número complexo é formado por uma parte real e uma parte imaginária.
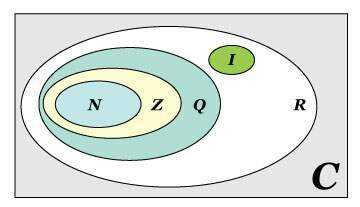
2- Como está sendo apresentado de forma visual na imagem desta 1ª Etapa, dentro do conjunto dos números complexos (C) estão os números: naturais (N), inteiros (Z), racionais (Q), irracionais (I), e os reais (R).
3- Um número negativo não possui raiz quadrada dentro do conjunto dos números reais(R). Contudo, dentro do conjunto dos números complexos (C), ele possui raiz.
4- De forma algébrica, representa-se um número complexo z da seguinte forma:
z=a+bi
5- A letra “i” representa a unidade imaginária.

2ª Etapa: Soma de números complexos

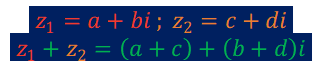
Quando estamos trabalhando com os conjuntos dos números naturais (N), inteiros (Z), racionais (Q), irracionais (I), e reais (R), podemos efetuar diversas operações matemáticas, tais como: adição, subtração, multiplicação e divisão.

Com o conjunto dos números complexos (C) não é diferente. Tais operações matemáticas também são bem definidas para o conjunto dos números complexos. Neste roteiro de estudos, veremos como efetuar a soma e a subtração entre números complexos.

Primeiramente, tratemos da soma:

Para se efetuar a soma entre dois (ou mais) números complexos, devemos somar os termos semelhantes, ou seja, somar a parte real do primeiro número complexo com a parte real do segundo número complexo, e somar a parte imaginária do primeiro número complexo com a parte imaginária do segundo número complexo. Vejamos um exemplo:

Para saber mais, assista:

Aprenda a somar Números Complexos – Marcos Aba Matemática
Acesso em 5 de agosto de 2021.

3ª Etapa: Subtração de números complexos

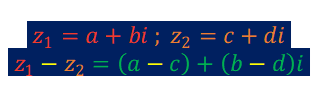
Ao trabalharmos com a subtração de números complexos, o procedimento é muito semelhante ao da soma. Ou seja, subtraímos a parte real do primeiro número complexo com a parte real do segundo número complexo, e somamos¹ com a subtração da parte imaginária do primeiro número complexo pela parte imaginária do segundo número complexo. Entretanto, deve-se ter uma maior atenção com os sinais durante tal operação matemática. Vejamos dois exemplos:

Exemplo 1:

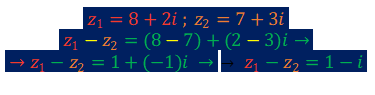
Exemplo 2:

Para saber mais, assista:

Aprenda a subtrair Números Complexos – Marcos Aba Matemática
Acesso em 5 de agosto de 2021.

¹ O sinal de mais (+) que aparece do lado direito da equação é devido ao fato da representação algébrica de um número complexo, por convenção, ser z=a+bi.

4ª Etapa: Cheque seus conhecimentos

Responder questões é um excelente exercício durante o estudo autodirigido. Abaixo, alguns exemplos sobre o tema estudado:

1) Qual a forma algébrica de z no caso 3z=z-(-8+6i)?
a) z = 4 – 2i
b) z = 4 – 3i
c) z = 2 – 2i
d) z = 1 – 2i

Alternativa B.

Resolução:
A forma algébrica de z é utilizada para representar um número complexo através da fórmula:

z=a+bi

Onde:
a é a parte real de z;

b é a parte imaginária de z.

Portanto:

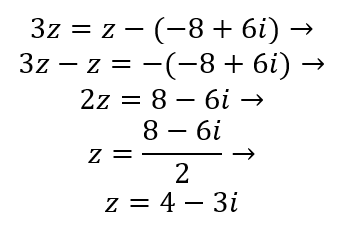
Logo, a forma algébrica de z no caso 3z=z-(-8+6i) é z=4-3i.

(Disponível em: Toda Matéria . Acesso em: 25 de julho de 2021).

2) Considere os seguintes números complexos z1 = 10 + 2i, z2 = 5 – 3i e z3 = – 9 + 5i e calcule a sua soma:
Resolução:
Vamos organizar os números complexos para somar de forma separada as partes reais e as partes imaginárias:
z1 + z2 + z3
(10 + 2i) + (5 – 3i) + (– 9 + 5i)
(10 + 5 – 9) + (2 – 3 + 5)i
6 + 4 i
Portanto, a soma dos complexos z1, z2 e z3 é igual a 6 + 4i.

(Disponível em: Brasil Escola . Acesso em: 25 de julho de 2021).

3) Calcule a subtração destes dois números complexos: z1 = 12 – 3i e z2 = 15 + 2i.
Resolução:
Organizando os números complexos para efetuar a subtração entre eles:
z1 – z2
(12 – 3i) – (15 + 2i)
(12 – 15) + (– 3 – 2)i
– 3 – 5i
A diferença dos complexos z1 e z2 é igual a – 3 – 5i.

(Disponível em: Brasil Escola . Acesso em: 25 de julho de 2021).

4) Qual o resultado obtido com a realização da soma e da subtração, respectivamente, dos números complexos z1 = 3 + i e z2 = 1 + 2i?
a) 2 + 3i e 1 – i
b) 3 + 2i e -4 – i
c) 4 + 3i e 2 – i
d) 1 + 2i e -3 – i

Alternativa C.

Resolução:

Operação de soma:
Z_1+Z_2=(a+c,b+d)

Na forma algébrica, temos:
(a+bi)+(c+di)=(a+c)+(b+d)i

Portanto:
Z_1+Z_2=(3+i)+(1+2i)→
Z_1+Z_2=(3+1)+(1+2)i→
Z_1+Z_2=4+3i

Operação de subtração:
Z_1-Z_2=(a-c,b-d)

Na forma algébrica, temos:
(a+bi)-(c+di)=(a-c)+(b-d)i

Portanto:
Z_1-Z_2=(3+i)-(1+2i)→
Z_1+Z_2=(3-1)+(1-2)i→
Z_1+Z_2=2-i

Sendo assim, a soma e a subtração dos números complexos z1 = 3 + i e z2 = 1 + 2i são, respectivamente, 4 + 3i e 2 – i.

(Disponível em: Toda Matéria . Acesso em: 25 de julho de 2021).

5) Quais os valores de x que resolvem a equação do 2º grau x2 + 4x + 5?
(Lembre-se que i2 = -1).
a) -2 + i e -2 – i
b) -1 + i e -1 – i
c) -2 + i e -1 + i
d) -1 + 2i e -1 + i

Alternativa A.

Resolução:
Para resolver a equação x²+4x+5 utilizaremos a fórmula de Bhaskara.

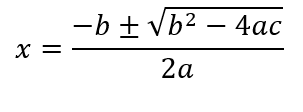
Como a = 1, b = 4 e c = 5, temos:

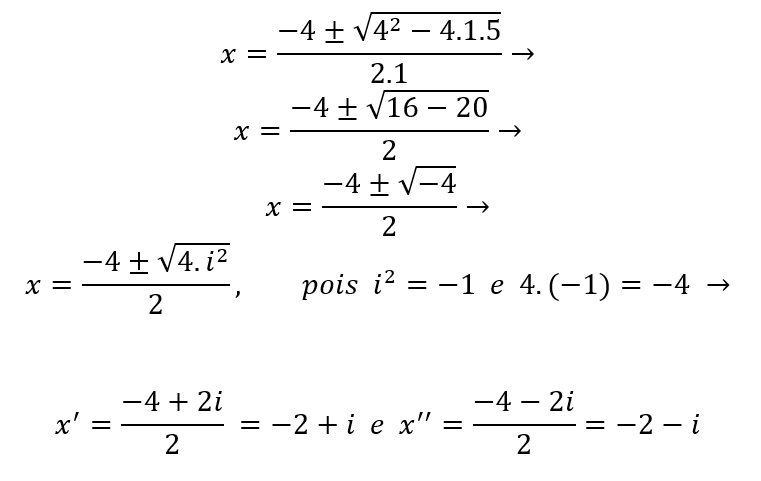
(Disponível em: Toda Matéria. Acesso em: 25 de julho de 2021).

Roteiro de estudos elaborado pelo prof. Elves Silva Moreira
Coordenação Pedagógica: profª. Dr.ª Aline Bitencourt Monge