Conteúdos
– Definição de um polinômio;
– Componentes de um polinômio;
– O que não é um polinômio;
– Classificação de polinômios;
– Valor numérico de um polinômio;
– Classes de polinômios;
– Operações com polinômios (adição, subtração, multiplicação e divisão).
Objetivos
– Aprender o que é um polinômio e seus componentes;
– Entender o que não é um polinômio;
– Aprender a obter o valor numérico de um polinômio;
– Aprender a reconhecer um polinômio nulo, completo e incompleto;
– Aprender a reconhecer um polinômio homogêneo e heterogêneo;
– Aprender a fazer operações com polinômios.
Proposta de trabalho:
O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos base e algumas propostas de atividades e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advém delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.
Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.
1ª Etapa: O que é um polinômio?
Fonte da imagem: O que é polinômio? – Brasil Escola
Perguntas norteadoras:
1) O que é um polinômio?
Polinômios – Toda Matéria – Rosimar Gouveia.
A partir da leitura do texto acima, responda às seguintes questões:
– Elabore em seu caderno uma breve definição de polinômio.
– O que é o coeficiente de um polinômio?
– O que é a parte literal de um polinômio?
– O que as letras de um polinômio representam?
– Considere o seguinte polinômio: 3x3 + 2x2 + x. Identifique seus coeficientes e sua parte literal.
Para saber mais, leia e assista:
O que é polinômio – Brasil Escola;
O que é um Polinômio – Professora Angela Matemática.
2) O que não é um polinômio?
Polinômios – Portal São Francisco.
A partir da leitura do texto anterior, resolva o seguinte exercício:
– Defina se as expressões algébricas são polinômios ou não polinômios. Caso sejam não polinômios, explique o motivo.
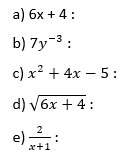
Para saber mais, assista:
O que é polinômio? E o que não é…? – Guilherme Félix (Professor de Matemática).
2ª Etapa: Classificação de polinômios

Fonte da imagem: Polinômios conceito e classificações – Vou Passar.Club
Pergunta norteadora:
1) Como podemos classificar os polinômios?
Polinômios – Mundo Educação – Naysa Crystine Nogueira Oliveira.
A partir da leitura do texto anterior, responda às seguintes perguntas:
– O que é um monômio? Dê um exemplo.
– O que é um binômio? Dê um exemplo.
– O que é um trinômio? Dê um exemplo.
– A partir de quantos termos uma expressão algébrica é chamada de polinômio?
Para saber mais, assista:
Classificação de expressões em: monômios, binômios, trinômios e polinômios – Matemática no papel.
3ª Etapa: Valor numérico de um polinômio

Fonte da imagem: Polinômios – Slideshare Professora Rosânia
Perguntas norteadoras:
1) Como obter o valor numérico de um polinômio?
Valor numérico de um Polinômio – Mundo Educação – Marcos Noé.
A partir da leitura do texto anterior, determine o valor numérico dos polinômios a seguir:
a) q(x) = x2 + 4x + 9, para x = 3.
b) q(x) = 3x3 + 8, para x = 2.
c) q(x) = 5x – 10, para x = 5.
Para saber mais, assista:
Valor numérico de um Polinômio – Luis Mundico Dantas.
2) Como identificar o grau de um polinômio?
Termos semelhantes e grau de Polinômios – Mundo Educação – Danielle de Miranda.
A partir da leitura do texto anterior, resolva às seguintes questões:
– O que são termos semelhantes em um polinômio?
– Identifique o grau dos polinômios a seguir:
a) Qual é o grau do monômio 9x5?
b) Qual é o grau do binômio 5x4 + 4x3?
c) Qual é o grau do trinômio 2x2 + 5x + 1?
d) Qual é o grau do polinômio xy6 – x2y4 + x3y2 – xy3 + xy?
Para saber mais, assista:
Grau de um Monômio e Grau de um Polinômio -Professora Angela Matemática;
Achando o grau do polinômio – Matemática no papel.
4ª Etapa: Classes de polinômios

Fonte da imagem: Classes de polinômios – Brasil Escola
Pergunta norteadora:
1) Quais são as classes para polinômios?
Classes de polinômios – Brasil Escola – Naysa Oliveira.
A partir da leitura do texto anterior, responda às seguintes questões:
– O que é um polinômio nulo? Dê um exemplo.
– O que é um polinômio homogêneo? Dê um exemplo.
– O que é um polinômio heterogêneo? Dê um exemplo.
– O que é um polinômio completo e ordenado? Dê um exemplo.
Para saber mais, assista:
Polinômio nulo e identidades – Kuadro Oficial;
Polinômios completos e incompletos – Matemática no papel.
5ª Etapa: Operações com polinômios

Fonte da imagem: Operações com Monômios e Polinômios – Slideplayer
Perguntas norteadoras:
1) Como efetuar a adição de polinômios?
Adição de polinômios – InfoEscola – Naysa Crystine Nogueira Oliveira.
A partir da leitura do texto anterior, resolva a seguinte situação:
– Adicione o polinômio P(x) = (5x + 18) ao polinômio Q(x) = (-10x – 9), ou seja, P(x) + Q(x).
Para saber mais, assista:
Adição de monômios e polinômios – Matemática no papel.
2) Como efetuar a subtração de polinômios?
Subtração de polinômios – InfoEscola – Naysa Crystine Nogueira Oliveira.
A partir da leitura do texto anterior, resolva a seguinte situação:
– Subtraia o polinômio P(x) = (x2 + 2x – 3) do polinômio Q(x) = x3 + x2 – 6, ou seja, P(x) – Q(x).
Para saber mais, assista:
Subtração de monômios e polinômios (Parte 1) – Matemática no papel;
Subtração de monômios e polinômios (Parte 2) – Matemática no papel.
3) Como efetuar a multiplicação de polinômios?
Multiplicação de Polinômios – InfoEscola – Naysa Crystine Nogueira Oliveira.
A partir da leitura do texto anterior, resolva a seguinte situação:
– Efetue a multiplicação do monômio P (x) = (12x) pelo polinômio
Q (x) = (2x3 + x3 – x + 3), ou seja, P (x) . Q (x).
Para saber mais, assista:
Multiplicação de polinômios – Professora Angela Matemática.
4) Como efetuar a divisão de polinômios?
Divisão de Polinômios – InfoEscola – Naysa Crystine Nogueira Oliveira.
A partir da leitura do texto anterior, resolva a seguinte situação:
– Divida o polinômio P (x) = (4x3 – 6x2 + 2x) pelo monômio Q (x) = (2x), ou seja, ![]() .
.
Para saber mais, assista:
Divisão de polinômios – Professora Angela Matemática.
6ª Etapa: Cheque seus conhecimentos
Realizar questões de vestibulares e do Enem é um excelente exercício durante o estudo autodirigido, isso porque essas questões são seguidas de gabarito, mesmo quando são dissertativas. Abaixo, alguns exemplos de questões sobre o tema estudado:
1) Classifique em monômios, binômios e trinômios, os polinômios abaixo:
a) 3abcd2
b) 3a + bc – d2
c) 3ab – cd2
Respostas:
a) monômio
b) trinômio
c) binômio
Fonte: Polinômios – Toda Matéria. Acesso em: 20 de julho de 2020.
2) Indique o grau dos polinômios:
a) xy3+ 8xy + x2y
b) 2x4+ 3
c) ab + 2b + a
d) zk7 – 10z2k3w6 + 2x
Respostas:
a) grau 4
b) grau 4
c) grau 2
d) grau 11
Fonte: Polinômios – Toda Matéria. Acesso em: 20 de julho de 2020.
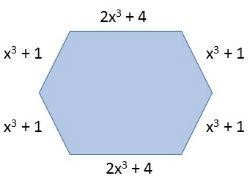
3) Qual o valor do perímetro da figura abaixo:
Resposta:
O perímetro da figura é encontrado somando-se todos os lados.
2x3 + 4 + 2x3 + 4 + x3 + 1 + x3 + 1 + x3 + 1 + x3 + 1 = 8x3 + 12
Fonte: Polinômios – Toda Matéria. Acesso em: 20 de julho de 2020.
4) Encontre a área da figura:
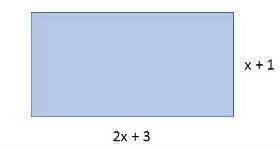
Resposta:
A área do retângulo é encontrada multiplicando-se a base pela altura.
(2x + 3) . (x+1) = 2x2 + 5x + 3
Fonte: Polinômios – Toda Matéria. Acesso em: 20 de julho de 2020.
5) Considerando que p(x) = 2x³ – kx² + 3x – 2k, para que valores de k temos p(2) = 4?
Resposta:
p(x) = 2x³ – kx² + 3x – 2k
p(2) = 4
2 . 2³ – k . 2² + 3 . 2 – 2k = 4
16 – 4k + 6 – 2k = 4
– 4k – 2k = – 16 – 6 + 4
– 6k = –18 . (–1)
6k = 18
k = 3
Temos que o valor de k é igual a 3.
Fonte: Exercícios sobre polinômios – Brasil Escola. Acesso em: 20 de Julho de 2020.
6) (FAAP–SP)
Calcule os valores de a, b e c para que o polinômio p(x) = a(x + c)³ + b(x + d) seja idêntico a p(x) = x³ + 6x² + 15x + 14.
Resposta:
a(x + c)³ + b(x + d) = x³ + 6x² + 15x + 14
a(x³ + 3x²c + 3xc² + c³) + bx + bd = x³ + 6x² + 15x + 14
ax³ + 3x²ac + 3axc² + ac³ + bx + bd = x³ + 6x² + 15x + 14
ax³ + 3x²ac + x(3ac² + b) + (ac³ + bd) = x³ + 6x² + 15x + 14
a = 1
3ac = 6
3ac² + b = 15
ac³ + bd = 14
Dessa forma:
3ac = 6
3 . 1 . c = 6
3c = 6
c = 2
3ac² + b = 15
3 . 1 . 2² + b = 15
12 + b = 15
b = 3
ac³ + bd = 14
1 . 2³ + 3 . d = 14
8 + 3d = 14
3d = 14 – 8
3d = 6
d = 2
Os números a, b e c são, respectivamente 1, 3 e 2.
Fonte: Exercícios sobre polinômios – Brasil Escola. Acesso em: 20 de Julho de 2020.
7) (MACK – SP)
Calcule os valores de m, n e l para os quais o polinômio p(x) = (2m – 1)x³ – (5n – 2)x² + (3 – 2l) é nulo.
Resposta:
2m – 1 = 0
2m = 1
m = 1/2
5n – 2 = 0
5n = 2
n = 2/5
3 – 2l = 0
–2l = –3
2l = 3
l = 3/2
Fonte: Exercícios sobre polinômios – Brasil Escola. Acesso em: 20 de Julho de 2020.