Conteúdos

●    Conjuntos numéricos;
●    Números Naturais;
●    Números Inteiros;
●    Números Racionais;
●    Números Irracionais;
●    Números Reais.

Objetivos

●    Compreender o que é um conjunto numérico;
●    Compreender quais são as características em comum entres os números que pertencem a um determinado conjunto numérico;
●    Aprender a identificar os subconjuntos de um determinado conjunto numérico.

Palavras-chave:

Conjuntos Numéricos. Naturais. Inteiros. Racionais. Irracionais. Reais.

Proposta de trabalho

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos base e algumas propostas de atividades, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.

Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advém delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: O que são os conjuntos numéricos

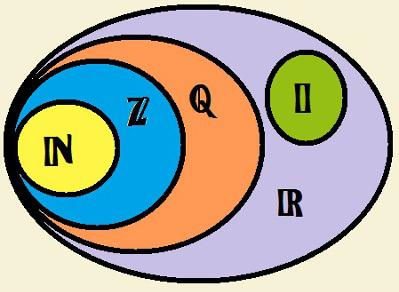
Pergunta norteadora:

O que são os conjuntos numéricos?

Conjuntos Numéricos
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/conjuntos-numericos/

A partir da leitura do texto acima, responda às seguintes perguntas:

1)    Elabore uma definição simples, com suas próprias palavras, para o conceito de Conjuntos Numéricos.
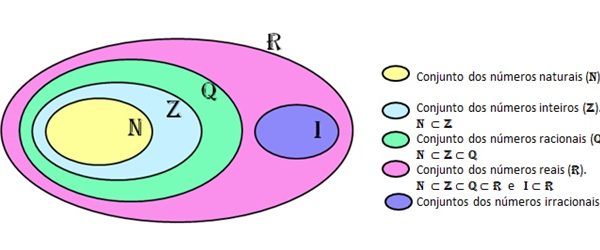
2)    Qual é a letra que representa o conjunto dos Números Naturais?
3)    Qual é a letra que representa o conjunto dos Números Inteiros?
4)    Qual é a letra que representa o conjunto dos Números Racionais?
5)     Qual é a letra que representa o conjunto dos Números Irracionais?
6)     Qual é a letra que representa o conjunto dos Números Reais?
7)    Qual é o ramo da Matemática que estuda os Conjuntos Numéricos?

Para saber mais, assista:

Conjuntos Numéricos – Matemática no Papel
Disponível em: https://youtu.be/wD7a9DAYb-4

2ª Etapa: Números Naturais (N)

Pergunta norteadora:

Quais são os números que formam o conjunto dos Números Naturais?

Números Naturais
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/numeros-naturais/

A partir da leitura do texto acima, responda às seguintes perguntas:

Os Números Naturais (N) formam um conjunto finito ou infinito?
Como podemos representar o conjunto dos Números Naturais Pares (N_P)?
Como podemos representar o conjunto dos Números Naturais Ímpares (N_Í)?
Todo e qualquer número par, ou ímpar, é um Número Natural?
Como podemos representar o Conjunto dos Números Naturais Não-Nulos ( N^*)?

Para saber mais, assista:

Números Naturais – Brasil Escola
Disponível em: https://youtu.be/kR2coFNP0_g

3ª Etapa: Números Inteiros (Z)

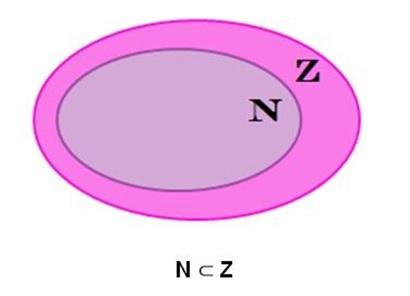
Pergunta norteadora:

Quais são os números que formam o conjunto dos Números Inteiros?

Números Inteiros
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/numeros-inteiros/

A partir da leitura do texto acima, responda às seguintes perguntas:

O conjunto dos Números Inteiros (Z) é finito ou infinito?
Como podemos representar o subconjunto dos Números Inteiros não-nulos (Z^*)?
Como podemos representar o subconjunto dos Números Inteiros não-negativos (Z_+)?
Como podemos representar o subconjunto dos Números Inteiros não-positivos (Z_-)?
Como podemos representar o subconjunto dos Números Inteiros positivos (Z_+^*)?
Como podemos representar o subconjunto dos Números Inteiros negativos (Z_-^*)?
Verdadeiro ou Falso?
(    ) O conjunto dos Números Naturais (N) é um subconjunto dos Números Inteiros (Z).
(    ) Todo Número Natural (N) é também um Número Inteiro (Z).
(    ) Todo Número Inteiro (Z) é também um Número Natural (N).

Para saber mais, assista:

O Conjunto dos Números Inteiros (Z)
Professora Angela Matemática
Disponível em: https://youtu.be/fmiw3ksXOmk

Resposta do Verdadeiro ou Falso: (V) (V) (F)

4ª Etapa: Números Racionais (Q)

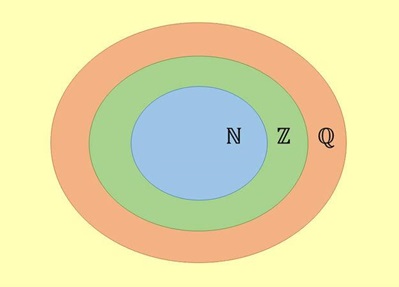
Pergunta norteadora:

Quais são os números que formam o conjunto dos Números Racionais?

Números Racionais
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/numeros-racionais/

A partir da leitura do texto acima, responda às seguintes perguntas:

O conjunto dos Números Racionais (Q) é finito ou infinito?
Como podemos representar o conjunto dos Números Racionais (Q)?
Como podemos representar o subconjunto dos Números Racionais não-nulos (Q^*)?
Como podemos representar o subconjunto dos Números Racionais não-negativos (Q_+)?
Como podemos representar o subconjunto dos Números Racionais não-positivos (Q_-)?
Como podemos representar o subconjunto dos Números Racionais negativos (Q_-^*)?
Como podemos representar o subconjunto dos Números Racionais positivos (Q_+^*)?
Verdadeiro ou Falso?
(    ) O conjunto dos Números Naturais (N) é um subconjunto dos Números Racionais     (Q).
(    ) O conjunto dos Números Inteiros (Z) é um subconjunto dos Números Racionais     (Q).
(    ) Toda dízima periódica é um Número Racional (Q).
(    ) O número π (Pi) é um Número Racional (Q).
(    ) Todo número decimal exato é um Número Racional (Q).

Para saber mais, assista:

Números Racionais
Brasil Escola
Disponível em: https://youtu.be/UZV0c4rblbY

Resposta do Verdadeiro ou Falso: (V) (V) (V) (F) (V)

5ª Etapa: Números Irracionais (I)

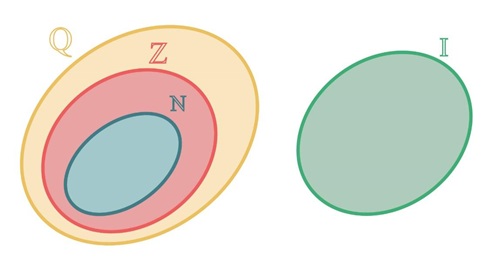
Pergunta norteadora:

Quais são os números que formam o conjunto dos Números Irracionais?

Números Irracionais
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/numeros-irracionais/

A partir da leitura do texto acima, responda às seguintes perguntas:

O conjunto dos Números Irracionais (I) é finito ou infinito?
O que é um Número Irracional Algébrico? Dê um exemplo.
O que é um Número Irracional Transcendente? Dê um exemplo.
Verdadeiro ou Falso?
(    ) O número Pi (π = 3,1415926…) é um Número Irracional Algébrico.
(    ) O número de Euler (e = 2,7182818…) é um Número Irracional Transcendente.
(    ) Não existe nenhum número que possa ser, ao mesmo tempo, Racional e Irracional.
(    ) Os Números Inteiros (Z) são um subconjunto dos Números Irracionais (I).

Para saber mais, assista:

Números Irracionais
Brasil Escola
Disponível em: https://youtu.be/wP9K2zIdVsM

Resposta do Verdadeiro ou Falso: (F) (V) (V) (F)

6ª Etapa: Números Reais (R)

Pergunta norteadora:

Quais são os números que formam o conjunto dos Números Reais?

Números Reais
Toda Matéria – Rosimar Gouveia
Disponível em: https://www.todamateria.com.br/numeros-reais/

A partir da leitura do texto acima, responda às seguintes perguntas:

O conjunto dos Números Reais (R) é finito ou infinito?
Verdadeiro ou falso?
(    ) O conjunto dos Números Naturais (N) é um subconjunto dos Números Reais (R).
(    ) O número Pi (π = 3,1415926…) não é um Número Real (R).
(    ) O conjunto dos Números Inteiros (Z) é um subconjunto dos Números Reais (R).
(    ) O conjunto dos Números Irracionais (I) é um subconjunto dos Números Inteiros (Z).
(    ) Uma dízima não periódica infinita não é um Número Real (R).
(    ) O conjunto dos Números Racionais (Q) é um subconjunto dos Números Reais (R).

Para saber mais, assista:

Conjunto dos Números Reais
Matemática Rio com Prof. Rafael Procópio
Disponível em: https://youtu.be/UqFr1kNQjPM

Resposta do Verdadeiro ou Falso: (V) (F) (V) (F) (F) (V)

7ª Etapa: Cheque seus conhecimentos

Realizar questões de vestibular e do ENEM é um excelente exercício durante estudo autodirigido, isso porque essas questões são seguidas de gabarito, mesmo quando são dissertativas. Abaixo, alguns exemplos de questões sobre o tema estudado:

            1) (FaeteC-RJ – 2015)

            Observe o segmento de reta abaixo, dividido em 5 segmentos congruentes:

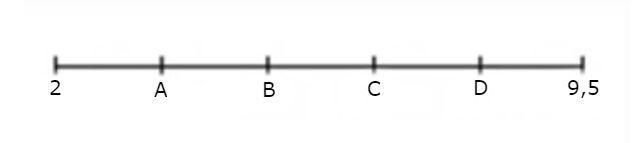
Nele estão representados seis números reais. A quantidade de elementos do conjunto {A, B, C, D} que representa número inteiro é:

a) 0
b) 1
c) 2
d) 3
e) 4

Resposta: C

Resolução:
Fazendo a diferença dos extremos do segmento de reta, temos:
9,5 – 2= 7,5

Dividindo o valor encontrado pelos 5 segmentos congruentes, temos:
7,5/5= 1,5

Significa que cada segmento vale 1,5. Sendo assim:
A=2+1,5 = 3,5
B=3,5+1,5 =5
C=5+1,5 = 6,5
D=6,5+1,5 = 8

Apenas B e D são números inteiros.

Disponível em: https://www.todamateria.com.br/numeros-inteiros/. Acesso em: 04 de outubro de 2020.

2) (UEL-PR) Observe os seguintes números:
I. 2,212121…
II. 3,212223…
III. π/5
IV. 3,1416
V. √(-4)

Assinale a alternativa que identifica os números irracionais:
a) I e II.
b) I e IV.
c) II e III.
d) II e V.
e) III e V.

Resposta: C

Resolução:
I. 2,212121… = É uma dízima periódica, portanto, é um número racional.
II. 3, 212223… = É uma dízima não periódica, portanto, é um número irracional.
III. π/5 = 0,6283185… = É uma dízima não periódica, portanto, é um número irracional.
IV. 3,1416 = É um número decimal exato, portanto, é um número racional.
V. √(-4) = É um número complexo.
Disponível em: https://www.todamateria.com.br/conjuntos-numericos/. Acesso em: 04 de outubro de 2020.

3) (Enem/2018) Para criar um logotipo, um profissional da área de design gráfico deseja     construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.

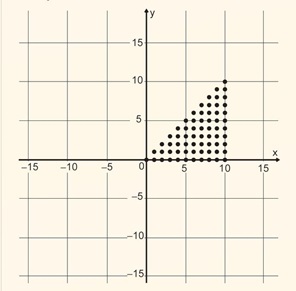
Nele estão representados seis números reais. A quantidade de elementos do conjunto {A, B, C, D} que representa número inteiro é:
Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever     algebricamente o conjunto que representa os pontos desse gráfico.

Esse conjunto é dado pelos pares ordenados (x; y) ∈ ℕ x ℕ, tais que

a) 0 ≤ x ≤ y ≤ 10
b) 0 ≤ y     ≤ x ≤ 10
c) 0 ≤ x ≤ 10, 0 ≤ y ≤ 10
d) 0 ≤ x + y ≤ 10
e) 0 ≤ x + y ≤ 20

Resposta: B
Justificativa:
Note que a figura expressa na questão, tanto no eixo y como no x, compreende os     números naturais (ℕ x ℕ) entre 0 e 10. Temos que: 0 ≤ y ≤ 10 e 0 ≤ x ≤ 10.

Assim: y = (0,1,2,3,4,5,6,7,8,9,10) e x = (0, 1,2,3,4,5,6,7,8,9,10). Entretanto, a figura     representada é um triângulo. Para satisfazer essa condição, nos pares ordenados y não poderá ser maior que x.

Veja que os valores de y são limitados pela igualdade com os valores de x, formando a     hipotenusa desse triângulo retângulo: (0;0), (1;1), (2;2), (3;3), (4;4), (5;5)…(10;10).

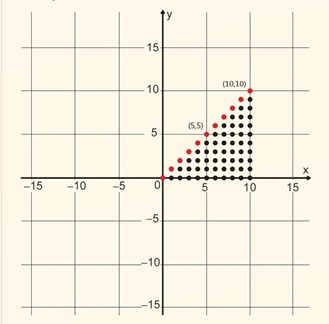
Desse modo, temos que: y ≤ x.
Logo, 0 ≤ y ≤ x ≤ 10.

Disponível em: https://www.todamateria.com.br/exercicios-de-conjuntos-numericos/. Acesso em: 04 de outubro de 2020.

4) Qual proposição abaixo é verdadeira?

a) Todo número inteiro é racional e todo número real é um número inteiro.

b) A intersecção do conjunto dos números racionais com o conjunto dos números irracionais tem 1 elemento.

c) O número 1,83333… é um número racional.

d) A divisão de dois números inteiros é sempre um número inteiro.

Resposta: C

Resolução:

a) Falsa. Realmente todo número inteiro é racional, pois pode ser escrito na forma de     fração. Por exemplo, o número – 7, que é inteiro pode ser escrito, na forma de fração, como -7/1. Contudo, nem todo número real é inteiro, por exemplo 1/2 não é um número inteiro.

b) Falsa. O conjunto dos números racionais não possui nenhum número em comum com os     irracionais, pois um número real ou é racional ou é irracional. Portanto, a intersecção é um     conjunto vazio.

c) Verdadeira. O número 1,83333… é uma dízima periódica, pois o algarismo 3 se repete     infinitamente. Esse número pode ser escrito na forma de fração como 11/6, portanto é um     número racional.

d) Falsa. Por exemplo, 7 dividido por 3 é igual a 2,33333…, que é uma dízima periódica,     logo não é um número inteiro.

Disponível em: https://www.todamateria.com.br/exercicios-de-conjuntos-numericos/. Acesso em: 04 de outubro de 2020.

5)  O valor da expressão abaixo, quando a = 6 e b = 9, é:

a) um número natural ímpar
b) um número que pertence ao conjunto dos números irracionais
c) não é um número real
d) um número inteiro cujo módulo é maior que 2
Resposta: D
Resolução:

Primeiro vamos substituir as letras pelos valores indicados e resolver a expressão:

Note que (- 6)2 é diferente de – 62, a primeira operação pode ser feita como:
(-6)2 = (- 6) . (-     6) = 36. Já sem os parênteses, apenas o 6 está elevado ao quadrado, ou seja    – 62 = – (6.6) = –    36.
Continuando a resolução, temos:

Observe que, como o índice da raiz é um número ímpar (raiz cúbica), existe raiz de número     negativo no conjunto dos números reais. Se o índice da raiz fosse um número par, o resultado seria um número complexo.

Agora, vamos analisar cada uma das opções apresentadas:

A opção a está errada, pois a resposta é um número negativo que não faz parte do conjunto dos números naturais.

O número – 3 não é um decimal não periódico infinito, portanto, não é um irracional, logo a     letra b também não é a solução correta.

A letra c também está errada, pois o número – 3 é um número pertencente ao conjunto dos     números reais.

A opção correta só pode ser a letra d e realmente o resultado da expressão é um número     inteiro e o módulo de -3 é 3 que é maior que 2.

Disponível em: https://www.todamateria.com.br/exercicios-de-conjuntos-numericos/. Acesso em: 04 de outubro de 2020.

Roteiro de estudos elaborado pelo Professor Elves Silva Moreira