Conteúdos
Este plano de aula de matemática expõe os conceitos fundamentais para trabalhar com juros compostos, no contexto da matemática financeira. Tópicos como: juros, montante, capital, taxa de juros, dentre outros, são discutidos ao longo do material. Ao final, em “Juros compostos e algumas aplicações”, apresentamos exercícios resolvidos detalhadamente. O material também conta com sugestões de textos e vídeos (em “Materiais relacionados”) para aprofundamento do/a professor(a).
● Introdução;
● Conceitos fundamentais;
● Fórmulas; e
● Juros compostos e algumas aplicações.
Objetivos
● Compreender a importância da matemática financeira;
● Compreender o significado matemático de conceitos como: juros, montante, capital e taxa de juros; e
● Aprender as principais diferenças entre uma capitalização sob regime de juros simples e sob regime de juros compostos.
Ensine também:
O que é potenciação e como ler uma potência?
Matemática financeira – Imposto de renda
Palavras-chave:
Capital. Juros. Montante. Taxa de juros. Juros simples. Juros compostos.
Sugestão de aplicação para o ensino remoto:
As sugestões a seguir estão organizadas em tópicos, com uma breve explicação de cada recurso.
● Jitsi Meet: É um sistema de código aberto e gratuito, com o objetivo de permitir a criação e implementação de soluções seguras para videoconferências via Internet, com áudio, discagem, gravação e transmissão simultânea. Possui capacidade para até 200 pessoas, não há necessidade de criar uma conta, você poderá acessar por meio do seu navegador ou fazer o download do aplicativo usando um celular .
Trabalhando com essa ferramenta, é possível:
– Compartilhar sua área de trabalho, apresentações e arquivos;
– Convidar usuários para uma videoconferência, por meio de um URL simples e personalizado;
– Editar documentos simultaneamente, usando Etherpad (editor de texto on-line de código aberto);
– Trocar mensagens, por meio do bate-papo integrado;
– Visualizar automaticamente o orador ativo ou escolher manualmente o participante que deseja ver na tela; e
– Reproduzir um vídeo do YouTube para todos os participantes.
● Gravação de videoaula usando o Power Point: O PPT, já tão utilizado por nós professores para preparamos nossas aulas, também permite a gravação de uma narração para os slides, que tanto nos auxiliam na explanação dos conteúdos. É possível habilitar a função de vídeo enquanto grava, de forma que os alunos verão o professor em uma janelinha no canto direito da apresentação. Essa ferramenta é bem simples e eficaz (veja o guia).
● Envio de Podcast aos alunos: Podcast nada mais é do que um áudio gravado (como os gravados no WhatsApp, por exemplo). Podem ser utilizados para narrar uma história, para corrigir atividades, revisar ou aprofundar os conteúdos. Para tanto, sugiro o aplicativo Anchor, que pode ser baixado em seu celular, muito simples de utilizar.
● Plataforma Google Classroom: O Classroom permite que você crie uma sala de aula virtual. Esta ação irá gerar um código que será compartilhado com os alunos, para que acessem a sala. Neste ambiente virtual, o/a professor/a poderá criar postagens de avisos, textos, slides do PPT, conteúdos, links de vídeos, roteiros de estudos, atividades etc. É uma forma bem simples e eficaz de manter a comunicação com os alunos e postar as aulas gravadas, usando os recursos anteriormente mencionados. Confira outros recursos oferecidos pela Google, como a construção de formulários (Google Forms) para serem realizados pelos alunos.
Sugerimos aulas com até 30 minutos de duração. Além disso, nem toda aula precisa gerar uma atividade avaliativa, para não sobrecarregar os alunos. As aulas virtuais também podem ser úteis para correção de exercícios e plantões de dúvidas.
Previsão para aplicação:
4 aulas (30 min./aula).
Para os conteúdos trazidos nas etapas 1 a 3, sugerimos o agendamento de duas a três aulas on-line síncronas com os alunos, por meio da plataforma Jitsi Meet, organizando os conteúdos em slides e compartilhando-os com os alunos com o recurso do compartilhamento de tela do seu computador, disponível na plataforma sugerida. Estimule a participação dos alunos pelo chat da plataforma, em uma aula expositiva dialogada. Caso a aula síncrona não seja possível, sugerimos a gravação de um vídeo com a narração dos slides, utilizando o Power Point.
Para a etapa 4, sugerimos que os exercícios indicados sejam montados usando o Google Formulários, e disponibilizados aos alunos por meio do Google Sala de aula. Os slides utilizados por você, professor(a), também podem ser disponibilizados aos alunos nessa plataforma. É importante reservar uma aula, após o prazo dado aos alunos para a realização da tarefa, para a correção e discussão das atividades propostas.
Você também pode elaborar, além dos exercícios, situações-problema (estudos de caso), tais como simulações de compra ações, imóveis ou veículos, para que os alunos analisem e discutam a melhor proposta de juros, por exemplo, tanto do ponto de vista do possível cliente quanto para o vendedor.
1ª Etapa: Introdução
“Ganhar” dinheiro nunca foi uma tarefa fácil. E, dependendo da condição socioeconômica da pessoa, tal tarefa pode tornar-se ainda mais complexa. Contudo, tão difícil quanto conseguir uma certa quantia de dinheiro é administrá-la bem.
Quando o assunto é dinheiro, diversas formas de abordagem são possíveis, sejam elas: econômica, social, histórica, geográfica, geopolítica etc.
Porém, neste plano de aula o objetivo é apresentar alguns conceitos disponibilizados pela matemática financeira para que sejamos capazes de melhor avaliar uma situação em que o nosso dinheiro esteja diretamente envolvido.
Em última análise, o que se objetiva aqui é disponibilizar ferramentas que facilitem a análise de como uma certa quantia de dinheiro evolui com o tempo.
Afinal de contas, se está cada vez mais difícil conseguir dinheiro (seja por meio de um trabalho formal ou informal), nada mais prudente do que buscar maneiras mais eficazes e responsáveis de gastá-lo, ou de investi-lo, sempre que possível.
2ª Etapa: Conceitos fundamentais
Para trabalharmos com a matemática financeira, é preciso compreender alguns conceitos fundamentais, tais como:
• Capital (C)
É o valor do dinheiro no momento presente, ou seja, o valor inicial. Ele serve de referência para efetuarmos os cálculos com os juros ao longo do tempo.
• Juros (J)
Representa o valor remunerado pelo capital empregado.
Os juros podem ser classificados em:
- Juros simples: mais utilizado em aplicações de curto prazo, a sua taxa é calculada sempre sobre o valor inicial do capital.
- Juros compostos: utilizado na maioria das aplicações financeiras, a sua taxa é calculada sobre o montante do período anterior.
• Taxa de juros (i)
Representa a percentagem cobrada sobre o capital a cada período. Ela pode ser aplicada de diferentes formas, tais como:
- (a.d.) = ao dia
- (a.m.) = ao mês
- (a.b.) = ao bimestre
- (a.a.) = ao ano
• Montante (M)
Trata-se do valor final da transação, ou seja, corresponde ao capital inicial somado com os juros.
• Tempo (n)
Representa o período que o capital ficará, ou ficou, aplicado. É de suma importância que as unidades de medida de tempo (n) e da taxa de juros (i) sejam as mesmas, para que os cálculos fiquem corretos.
• Lucro
Corresponde ao valor ganho numa transação comercial.
• Desconto
Corresponde ao valor subtraído de uma transação comercial em relação à taxa de juros (i) do capital.
• Acréscimo
Corresponde ao valor somado de uma transação comercial em relação à taxa de juros (i) do capital.
De posse desses conceitos fundamentais, a partir de agora somos capazes de manipular/trabalhar com algumas fórmulas bastante recorrentes na matemática financeira.
3ª Etapa: Fórmulas
Quando estamos lidando com uma transação financeira cuja capitalização é feita segundo o regime de juros simples, utilizamos a seguinte fórmula:
![]()
Onde,
J→ juros simples
C→capital aplicado
i→taxa de juros
n→período que o capital ficará aplicado
O montante para este tipo de aplicação é:
![]()
Ou seja,
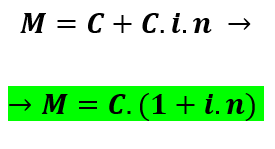
Já quando estamos lidando com uma transação cuja capitalização é feita segundo o regime de juros compostos, utilizamos a seguinte fórmula:
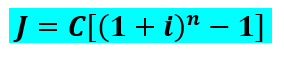
Onde,
J→ juros compostos
C→capital aplicado
i→taxa de juros
n→período que o capital ficará aplicado
E o montante para este tipo de aplicação é:
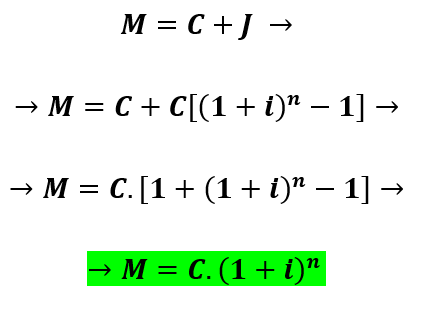
Fazendo uma rápida análise das fórmulas acima, fica claro que o montante de uma aplicação com capitalização feita sob regime de juros compostos cresce mais rapidamente do que o montante de uma aplicação com capitalização feita sob regime de juros simples, pois a fórmula para o primeiro é representada por uma função exponencial, enquanto a fórmula do segundo é representada por uma função afim, ou seja, do 1º grau.
A partir de agora, daremos maior atenção para o tipo de capitalização que é aplicada sob o regime de juros compostos.
4ª Etapa: Juros compostos e algumas aplicações
Como já foi dito, a maioria das transações financeiras do dia a dia envolve situações cuja capitalização é feita sob o regime de juros compostos. Seja o financiamento de uma casa, a compra de um automóvel, um empréstimo no banco ou uma compra parcelada de um eletrodoméstico com o cartão de crédito, dentre tantas outras transações possíveis, todas elas envolvem juros compostos.
Vamos agora manipular as fórmulas relacionadas a esse tipo de regime, a partir de alguns exercícios, para adquirirmos algum grau de familiaridade com tal conteúdo.
Exercícios:
01) Aplicando hoje na caderneta de poupança a quantia de R$ 20.000,00, qual será o montante gerado ao final de 4 anos, sabendo que a rentabilidade mensal é de 0,5%?
Resolução:
I) Primeiramente, vamos identificar os dados fornecidos pelo exercício:
Capital aplicado: R$ 20.000,00. Portanto:
C=R$ 20 000,00
Taxa de juros: 0,5% mensal. Passando a taxa para a representação unitária, que é a taxa percentual dividida por 100, sem o símbolo %, temos:
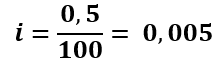
Neste ponto, devemos tomar bastante cuidado, pois a taxa de juros (i) e o período (n) estão em unidades de medida distintas.
Período que o capital ficará aplicado: 4 anos. Fazendo a conversão, temos que, como cada ano tem 12 meses:
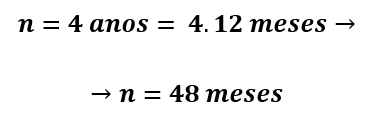
O exercício está nos pedindo o montante:
M=?
II) Agora que já identificamos todos os dados fornecidos pelo exercício, fizemos as devidas conversões e sabemos exatamente o que se pede, podemos utilizar a fórmula para o cálculo do montante para juros compostos:
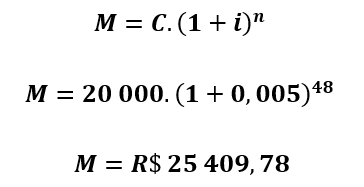
(Disponível em: Brasil Escola . Acesso em: 19 de junho de 2021).
02) Determinado capital gerou, após 24 meses, um montante de R$ 15.000,00. Sabendo que a taxa de juros é de 2% ao mês, determine o valor desse capital.
Resolução:
I) Identificando os dados fornecidos pelo exercício:
Montante: R$ 15.000,00. Portanto:
M=R$ 15 000,00
Período em que o capital ficou aplicado: 24 meses. Ou seja:
n=24 meses
Taxa de juros: 2% ao mês. Neste caso, tanto a taxa de juros (i) quanto o período (n) estão com a mesma unidade de medida. Passando a taxa de juros para a representação unitária, temos:
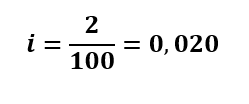
O exercício pede o capital, portanto:
C=?
II) Isolando o capital na fórmula, temos:
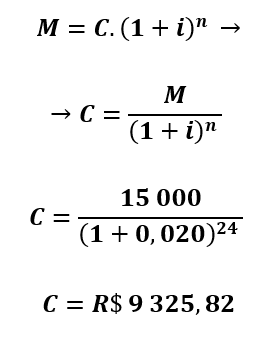
(Disponível em: Brasil Escola . Acesso em: 19 de junho de 2021).
03) Um capital de R$ 5.000,00, aplicado durante um ano e meio, produziu um montante de R$ 11.000,00. Determine a taxa de juros dessa aplicação.
Resolução:
I) Identificando os dados fornecidos pelo exercício:
Capital aplicado: R$ 5.000,00. Ou seja:
C=R$ 5 000,00
Montante: R$ 11.000,00. Portanto:
M=R$ 11 000,00
Período em que o capital ficou aplicado: um ano e meio. Como um ano tem 12 meses, e metade de um ano tem 6 meses, temos:
n=18 meses
O exercício pede a taxa de juros:
i=?
II) Manipulando a fórmula, temos:
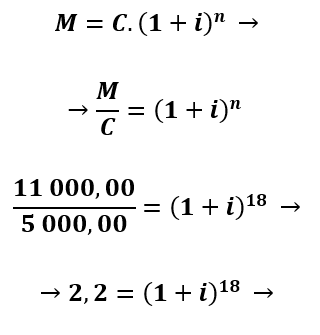
Agora, precisamos tirar a raiz dos dois lados:
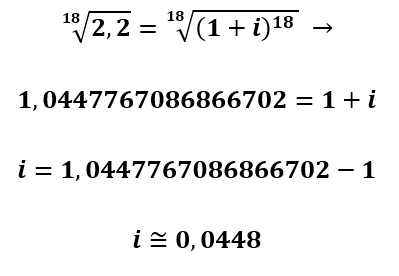
ou
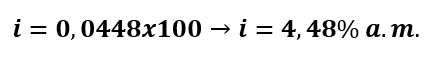
(Disponível em: Brasil Escola . Acesso em: 19 de junho de 2021).
Plano de aula elaborado pelo professor Elves Silva Moreira.
Adaptação para o ensino remoto elaborada pela prof.ª Dr.ª Nathalie Lousan.
Coordenação Pedagógica: prof.ª Dr.ª Aline Bitencourt Monge
Materiais Relacionados
• Para ler conteúdos sobre matemática financeira – juros compostos:
Brasil Escola – Juros compostos
Acesso em: 19 de junho de 2021.
Matemática financeira – conceitos
Acesso em: 19 de junho de 2021.
Só Matemática
Acesso em: 19 de junho de 2021.
Educa Mais Brasil – Matemática financeira
Acesso em: 19 de junho de 2021.
Matemática financeira
Acesso em: 19 de junho de 2021.
Mundo educação – Matemática financeira
Acesso em: 19 de junho de 2021.
• Para ver vídeos sobre matemática financeira – juros compostos:
Juros compostos – Matemática Financeira – Equaciona com Paulo Pereira
Acesso em: 19 de junho de 2021.
Juros compostos – Matemática no Papel
Acesso em: 19 de junho de 2021.
Juros simples e juros compostos – Descomplica
Acesso em: 19 de junho de 2021.

