Conteúdos
Este plano de aula de matemática apresenta de forma introdutória o que é fatoração, concentrando-se em alguns casos particulares, tais como: fatoração numérica, fator comum em evidência, e fatoração por agrupamentos. Ao longo do material, diversos exemplos são apresentados e resolvidos, com todo o passo a passo. O material também conta com algumas sugestões de textos e vídeos (em “Materiais Relacionados”) para que o/a professor(a) possa buscar um maior aprofundamento sobre o assunto.
● Fatoração numérica;
● Fator comum em evidência; e
● Fatoração por agrupamento.
Objetivos
● Compreender o que é a fatoração;
● Aprender a fatorar um número; e
● Aprender alguns casos relevantes de fatoração.
Ensine também:
Radiciação: representação e propriedades
Números primos e números compostos
Palavras-Chave:
Fatoração. Fatoração numérica. Fator comum em evidência. Fatoração por agrupamento.
Sugestão de aplicação para o ensino remoto:
As sugestões a seguir estão organizadas em tópicos, com uma breve explicação de cada recurso.
● Jitsi Meet: É um sistema de código aberto e gratuito, com o objetivo de permitir a criação e implementação de soluções seguras para videoconferências via Internet, com áudio, discagem, gravação e transmissão simultânea. Possui capacidade para até 200 pessoas, não há necessidade de criar uma conta, você poderá acessar por meio do seu navegador ou fazer o download do aplicativo usando um celular .
Trabalhando com essa ferramenta, é possível:
– Compartilhar sua área de trabalho, apresentações e arquivos;
– Convidar usuários para uma videoconferência, por meio de um URL simples e personalizado;
– Editar documentos simultaneamente, usando Etherpad (editor de texto on-line de código aberto);
– Trocar mensagens, por meio do bate-papo integrado;
– Visualizar automaticamente o orador ativo ou escolher manualmente o participante que deseja ver na tela; e
– Reproduzir um vídeo do YouTube para todos os participantes.
● Gravação de videoaula usando o Power Point: O PPT, já tão utilizado por nós professores para preparamos nossas aulas, também permite a gravação de uma narração para os slides, que tanto nos auxiliam na explanação dos conteúdos. É possível habilitar a função de vídeo enquanto grava, de forma que os alunos verão o professor em uma janelinha no canto direito da apresentação. Essa ferramenta é bem simples e eficaz (veja o guia).
● Envio de Podcast aos alunos: Podcast nada mais é do que um áudio gravado (como os gravados no WhatsApp, por exemplo). Podem ser utilizados para narrar uma história, para corrigir atividades, revisar ou aprofundar os conteúdos. Para tanto, sugiro o aplicativo Anchor, que pode ser baixado em seu celular, muito simples de utilizar.
● Plataforma Google Classroom: O Classroom permite que você crie uma sala de aula virtual. Esta ação irá gerar um código que será compartilhado com os alunos, para que acessem a sala. Neste ambiente virtual, o/a professor/a poderá criar postagens de avisos, textos, slides do PPT, conteúdos, links de vídeos, roteiros de estudos, atividades etc. É uma forma bem simples e eficaz de manter a comunicação com os alunos e postar as aulas gravadas, usando os recursos anteriormente mencionados. Confira outros recursos oferecidos pela Google, como a construção de formulários (Google Forms) para serem realizados pelos alunos.
Sugerimos aulas com até 30 minutos de duração. Além disso, nem toda aula precisa gerar uma atividade avaliativa, para não sobrecarregar os alunos. As aulas virtuais também podem ser úteis para correção de exercícios e plantões de dúvidas.
Proposta de trabalho:
Para os conteúdos trazidos nas etapas 1 a 7, sugiro o agendamento de 4 a 5 aulas on-line síncronas com os alunos, por meio da plataforma Jitsi Meet, organizando os conteúdos em slides e compartilhando-os com os alunos com o uso do recurso do compartilhamento de tela do seu computador, disponível na plataforma sugerida. Estimule a participação dos alunos pelo chat da plataforma, em uma aula expositiva dialogada. Caso a aula síncrona não seja possível, sugiro a gravação de um vídeo com a narração dos slides, utilizando o Power Point.
Para as etapas 8 e 9, sugiro que os exercícios sejam organizados no Google Formulários, e disponibilizados aos alunos por meio do Google Sala de aula. Os slides utilizados nas outras etapas também podem ser disponibilizados aos alunos nessa plataforma. É importante reservar uma aula, após o prazo dado aos alunos para a realização da tarefa, para a correção e discussão das atividades propostas.
Previsão para aplicação:
5 aulas (30 min./aula)
1ª Etapa: Fatoração numérica
Fator(ação)
Fatorar um número consiste em o decompor em um produto de fatores primos. Ou seja, dado um certo número, para o fatorarmos, é preciso encontrar quais são os números primos que, multiplicados, resultam nele.
Lembrando que: um número natural primo é aquele que possui apenas dois divisores naturais (N), a dizer: o número 1 e ele próprio .
Alguns exemplos de números primos:
2→ é o único número par e primo, pois só pode ser dividido por 1 e por ele mesmo.
3→ é primo, pois só pode ser dividido por 1 e por ele mesmo.
4→ não é primo, pois pode ser dividido por 1,por 2 e por ele mesmo.
5→ é primo, pois só pode ser dividido por 1 e por ele mesmo.
Fatoração numérica de 360
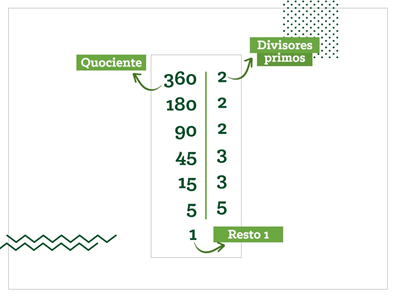
Note que do lado direito do segmento de reta vertical só aparecem números primos. Figura disponível em COC.
Para fatorar um número n, geralmente, o procedimento consiste em:
| Número n a ser fatorado | Menor número primo divisor de n |
Cria-se um esquema em que se separa por um segmento de reta vertical o número n a ser fatorado dos fatores primos que são seus divisores, sempre começando do menor divisor primo.
Efetua-se, então, a divisão do número n pelos seus divisores primos até se obter como resultado final o número 1.
Exemplos:
1) Vamos fatorar o número 27:
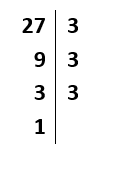
O número 27 não é par e, portanto, não pode ser dividido por 2, que é o menor número natural primo. O próximo número natural primo é 3. Começamos, então, dividindo o número 27 por 3. Logo após, pegamos o resultado, que é 9, e procuramos novamente o menor número natural primo que possibilita continuar a divisão, ou seja, dividimos por 3 novamente. Por fim, pegamos o resultado da última divisão, 3, e o dividimos por 3 mais uma vez, obtendo-se do lado esquerdo o resultado igual a 1.
Ou seja, ao fatorarmos o número 27, encontramos uma nova forma de escrevê-lo/representá-lo:
27=3.3.3
Ou ainda,
27=3³
2) Agora, vamos fatorar o número 45:
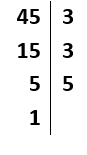
O procedimento aqui é muito semelhante ao exemplo anterior.
Novamente, ao fatorarmos o número 45, encontramos novas formas de representá-lo:
45= 3.3.5
Ou,
45=3².5
3) Fatoremos, agora, o número 120:
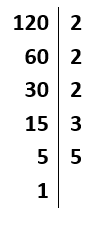
Neste caso, como o número 120 é par, começamos a divisão pelo menor número primo natural, que é 2. Pegamos o resultado, 60, que também e par, e o dividimos por 2 novamente. O procedimento continua, com a divisão do resultado da última divisão, 30, também par, por 2. Agora, considerando que obtivemos como resultado um número ímpar, 15, buscamos o próximo número primo natural que é divisor de 15, ou seja, 3. Obtemos, assim, como resposta o número 5, que é primo e, portanto, só pode ser dividido por 1 e por ele mesmo. Dividindo 5 por 5, obtemos do lado esquerdo resto igual a 1, o que significa que finalizamos a fatoração do número 120.
Desta forma, podemos reescrever o número 120 da seguinte maneira:
120=2.2.2.3.5
Ou ainda,
120=2³.3.5
2ª Etapa: Fator comum em evidência
Da mesma forma que podemos reescrever um determinado número n a partir da fatoração numérica, é possível também reescrever certas expressões matemáticas, identificando o fator em comum a duas ou mais parcelas da expressão matemática em questão.
Exemplos:
1) Vejamos a expressão a seguir:
2a+4b +6c
Podemos reescrever a expressão matemática acima da seguinte forma:
2a+2.2b+2.3c
Pois:
4b=2.2b , e 6c=2.3c
Agora, destacamos o fator que existe em comum a todas as três parcelas da expressão dada:
2a+2.2b+2.3c
Percebemos que o fator em comum a todas as parcelas é o número 2. Para fatorar a expressão, colocamos o número 2 em evidência, e repetimos, entre parênteses, os termos das parcelas que restaram:
2 (a+2b+3c)
Isso significa que:
2a+4b +6c=2 .(a+2b+3c)
Se quisermos reescrever a parte direita da igualdade acima como está expressa do lado esquerdo, basta aplicarmos a propriedade distributiva da multiplicação.
Fatorar a expressão 2a+4b +6c é igual a, após identificarmos o fator em comum a todas as parcelas da expressão, colocar entre parênteses (multiplicando o termo em comum) o resultado da divisão de cada uma das parcelas pelo fator em comum, ou seja:
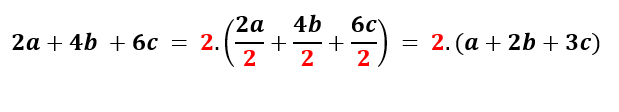
2) Vejamos a seguinte expressão matemática com duas parcelas:
3x+ 6
Vamos reescrever a expressão acima da seguinte forma:
3x+ 2.3
Agora, vamos destacar o fator em comum às duas parcelas da expressão anterior:
3x+ 2.3
Colocando o fator comum em evidência, e os demais termos entre parênteses, temos:
3 .(x+ 2)
Isso significa que:
3x+ 6=3 .(x+ 2)
Novamente, se quisermos reescrever o lado direito da igualdade como está escrito do lado esquerdo, basta aplicarmos a propriedade distributiva da multiplicação.
Mais uma vez, fatorar a expressão 3x+6 é igual a, após identificarmos o fator em comum a todas as parcelas da expressão, colocar entre parênteses (multiplicando o fator em comum) o resultado da divisão de cada uma das parcelas pelo fator em comum:
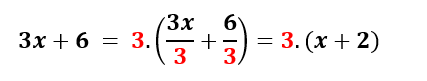
3) Mais um exemplo com uma expressão matemática com duas parcelas:
8a²+4a³
Vamos reescrever a expressão acima da seguinte forma:
2.4.a²+4.a².a
Pois:
8a²=2.4.a² , e 4a³=4.a².a
Neste momento, vamos identificar o fator em comum às duas parcelas:
2.4.a²+4.a².a
Colocando-o em evidência e, repetindo o que restou entre parênteses, temos:
4.a².(2+a)
Ou seja:
8a²+4a³=4.a².(2+a)
Naturalmente, ao aplicarmos a propriedade distributiva da multiplicação do lado direito da igualdade da expressão acima, obteremos o mesmo valor que está do lado esquerdo da igualdade.
Considerando 8a²+4a³ , se dividirmos as duas parcelas pelo fator em comum, chegaremos ao valor que está entre parênteses na expressão anterior:
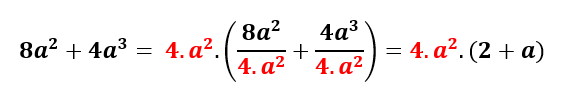
3ª Etapa: Fatoração por agrupamento
Ao trabalharmos com expressões matemáticas mais complexas, é possível encontrar um fator em comum entre algumas parcelas de uma dada expressão, e um outro fator em comum entre as demais parcelas da mesma expressão. Isso significa que devemos agrupar algumas parcelas que possuem um certo fator em comum, e as demais parcelas devem ser agrupadas com um outro fator em comum, ou seja, devemos aplicar a fatoração da etapa anterior mais de uma vez.
Exemplos:
1) Vejamos a seguinte expressão matemática, que possui quatro parcelas:
ax+bx+ ad+bd
Vamos dividir a expressão anterior em dois grupos. O primeiro grupo será formado pelas parcelas que possuem o termo x, e o segundo grupo será aquele formado pelas parcelas que possuem o termo d.
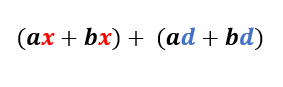
Aplicando a fatoração para um fator comum em evidência no primeiro grupo, temos:
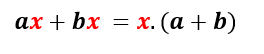
E aplicando a fatoração para um fator comum em evidência no segundo grupo, temos:
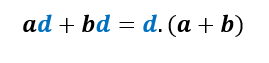
Ou seja:
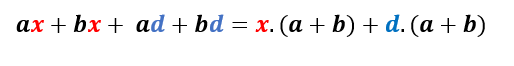
Mas notemos que, do lado direito da igualdade, existe um termo em comum que multiplica tanto o x quanto o d . Ou seja, podemos aplicar a fatoração para um fator comum em evidência mais uma vez:
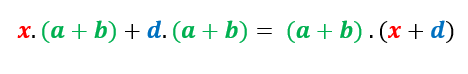
O que significa que:
ax+bx+ ad+bd=(a+b) .(x+d)
Aplicando-se a propriedade distributiva da multiplicação do lado direito da igualdade, podemos conferir que o resultado é o mesmo que o do lado esquerdo.
2) Vejamos mais um exemplo, envolvendo uma expressão matemática com quatro parcelas:
6y-4ay- 9b+6ab
Reescrevendo essa expressão, temos:
2.3.y-2.2.a.y- 3.3.b+2.3.a.b
Agora, vamos dividir a expressão acima em dois grupos. O primeiro grupo será formado pelas parcelas que possuem o termo y, e o segundo grupo será aquele formado pelas parcelas que possuem o termo b.

Percebemos que, do lado direito da igualdade, existe um fator em comum que multiplica tanto o 2y quanto o 3b. Ou seja, podemos aplicar aqui a fatoração para um fator comum em evidência mais uma vez:
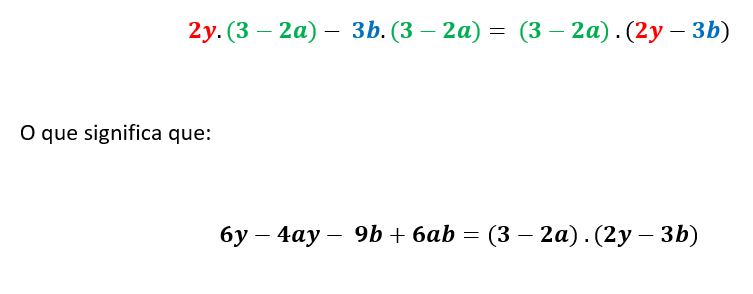
Plano de aula elaborado pelo Professor Elves Silva Moreira
Adaptação para o ensino remoto elaborada pela Prof.ª Dr.ª Nathalie Lousan
Materiais Relacionados
• Para ver conteúdos sobre Fatoração:
Matemática básica (p. 71-77)
Acesso em: 18 de abril de 2021.
Fatoração – simplificação de equações matemáticas
Acesso em: 18 de abril de 2021.
Fatoração
Acesso em: 18 de abril de 2021.
• Para ver vídeos sobre Fatoração:
Fatoração (Matemática Básica) – Matemática Show com Prof. Abraão
Acesso em: 18 de abril de 2021.
O que é Fatoração? – Aprenda a fatorar números – Curso Enem Gratuito
Acesso em: 18 de abril de 2021.
Fatoração 01 – Fator comum em evidência – Matemática no Papel
Acesso em: 18 de abril de 2021.
Fatoração 04 – Fatoração por Agrupamento – Matemática no Papel
Acesso em: 18 de abril de 2021.
Fatoração (C/ exemplos) – Tópicos em Álgebra – Equaciona Com Paulo Pereira
Acesso em: 18 de abril de 2021.

