Conteúdos
● Número primo;
● Número composto;
● Crivo de Eratóstenes.
Objetivos
● Compreender o que é um número primo e um número composto;
● Aprender como identificar um número primo e um número composto;
● Aprender como encontrar números primos a partir do Crivo de Eratóstenes.
Palavras-Chave:
Números primos. Números compostos. Teorema Fundamental da Aritmética. Crivo de Eratóstenes.
Sugestão de aplicação no ensino remoto:
As sugestões estão organizadas em tópicos com uma breve explicação de cada recurso.
● Jitsi Meet: é um sistema de código aberto e gratuito, com o objetivo de permitir a criação e implementação de soluções seguras para videoconferências via Internet, com áudio, discagem, gravação e transmissão simultânea. Possui capacidade para até 200 pessoas, não há necessidade de criar uma conta, você poderá acessar através do seu navegador ou fazer o download do aplicativo, disponível para Android e iOS.
Trabalhando com essa ferramenta, é possível:
– Compartilhar sua área de trabalho, apresentações e arquivos;
– Convidar usuários para uma videoconferência por meio de um URL simples e personalizado;
– Editar documentos simultaneamente usando Etherpad (editor de texto on-line de código aberto);
– Trocar mensagens através do bate-papo integrado;
– Visualizar automaticamente o orador ativo ou escolher manualmente o participante que deseja ver na tela;
– Reproduzir um vídeo do YouTube para todos os participantes.
● Gravação de videoaula usando o Power Point: o PPT, já tão utilizado por nós professores para preparamos nossas aulas, também permite a gravação de uma narração para os slides, que tanto nos auxiliam na explanação dos conteúdos. É possível habilitar a função de vídeo enquanto grava, assim, os alunos verão o professor em uma janelinha no canto direito da apresentação. Essa ferramenta é bem simples e eficaz. Veja um guia.
● Envio de Podcast aos alunos: podcast nada mais é do que um áudio gravado (como os enviados pelo Whatsapp). Podem ser utilizados para narrar uma história, para correção de atividades, revisar ou aprofundar os conteúdos. Para tanto, sugiro o app Anchor, que pode ser baixado no seu celular. Ele é muito fácil e simples de utilizar.
● Plataforma Google Classroom: permite a criação de uma sala de aula virtual. Essa ação irá gerar um código que será compartilhado com os alunos, para que acessem a sala. Nesse ambiente virtual, o/a professor/a poderá criar postagens de avisos, textos, slides do PPT, conteúdos, links de vídeos, roteiros de estudos, atividades, etc. É uma forma bem simples e eficaz de manter a comunicação com os alunos e postar as aulas gravadas, usando os recursos anteriormente mencionados. Confira outros recursos oferecidos pela Google, como a construção de formulários (Google Forms) para serem realizados pelos alunos.
Sugerimos aulas com até 30 minutos de duração. Além disso, nem toda aula precisa gerar uma atividade avaliativa, para não sobrecarregar os alunos. As aulas virtuais também podem ser úteis para correção de exercícios e plantões de dúvidas.
Previsão para aplicação:
3 aulas (30 min./aula)
1ª Etapa: Início de conversa
O/A professor/a poderá começar a aula, que deverá acontecer através da plataforma Jitsi Meet, fazendo as seguintes perguntas (desafio!) para os/as estudantes:
1) Quem sabe o que é o conjunto dos números naturais (N)?
2) Quem sabe o que é um número primo? Quais são suas características?
3) E os números compostos, quais são? Quais são suas características?
4) Alguém conhece alguma aplicação na área de tecnologia da informação (TI), para os números primos?
5) Quem sabe qual é o único número natural par, que também é primo?
Os/As alunos/as podem responder por áudio ou de forma escrita, através do chat da plataforma. A partir dessas perguntas, o/a professor/a poderá identificar qual é o nível de conhecimento da classe sobre o assunto, e iniciar uma discussão mais aprofundada sobre o tema.
Após o debate, o/a professor/a poderá expor os conteúdos com auxílio de slides (que podem ser preparados com os textos e imagens disponibilizados abaixo) e projetados por meio do recurso de compartilhamento de tela do seu computador. Tais conteúdos podem ser organizados em três aulas expositivas virtuais.
Ao final das três aulas, espera-se que a própria classe seja capaz de responder todas as perguntas anteriores.
2ª Etapa: O que é um número primo?

Pode-se definir um Número Primo (p), onde p > 1, como sendo todo aquele Número Natural (N) que possui apenas dois¹ divisores: o número 1 e ele mesmo (p), onde o resultado também é um Número Natural (N).
Ou seja, se p só puder ser dividido da seguinte forma:
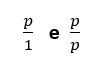
Exemplo:
Quais são os Números Primos entre 1 e 10?
1) Não é Primo².
2) É Primo! O único número Par, que também é Primo. Pois:

3) É Primo. Possui apenas dois divisores:

4) Não é Primo. Possui três divisores:
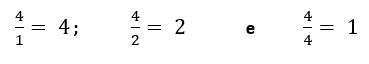
5) É Primo. Possui apenas dois divisores:
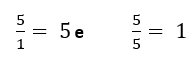
6) Não é Primo. Possui quatro divisores:
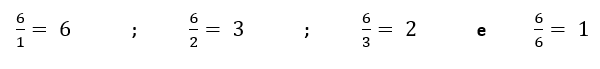
7) É Primo. Possui apenas dois divisores:
![]()
8) Não é Primo. Possui quatro divisores:
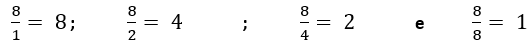
9) Não é Primo. Possui três divisores:
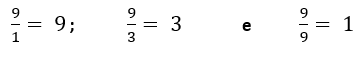
10) Não é Primo. Possui quatro divisores:
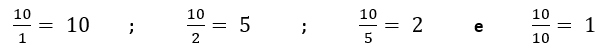
Portanto, entre 1 e 10 existem quatro Números Primos, que são: {2; 3; 5 e 7}.
¹ Existem alguns autores que definem os Números Primos a partir do conjunto numérico dos números inteiros (Z). Nesta definição, o número primo (p) possui quatros divisores: -1, 1, – p e p.
² Obs.: É importante destacar que o número 1 não é um número primo. Pode-se justificar isso de algumas maneiras:
● Justificativa histórica: Durante vários séculos, diversos matemáticos importantes debateram sobre o fato do número 1 ser, ou não, primo. Contudo, a partir da década de 40 do século XX, convencionou-se que o número 1 não é primo;
● O número 1 faz parte da própria definição de um número primo (p);
● O número 1 possui apenas um divisor, e não dois divisores, pois p = 1, ou seja, ele próprio;
● Se considerar o número 1 como não primo, o Teorema Fundamental da Aritmética é válido. O que equivale a dizer que, caso o número 1 fosse primo, o Teorema Fundamental da Aritmética não seria válido.
3ª Etapa: O que é um número composto?

É possível definir o conjunto dos Números Compostos por “exclusão”, ou seja:
Todo número que não é Primo, é um Número Composto.
Ao se utilizar o Teorema Fundamental da Aritmética, pode-se fazer uma definição ainda mais precisa.
O que o Teorema Fundamental da Aritmética diz, é basicamente o seguinte:
“Todo número natural maior que 1 ou é primo
ou pode ser escrito como produto de números primos.”
Dessa forma, caso o número 1 também fosse considerado como primo, o Teorema Fundamental da Aritmética não seria válido, pois isso permitiria que os números compostos (não primos) fossem escritos de uma maneira não única, como um produto de números primos.
Exemplo:
O número 35 pode ser escrito como:
35=5.7
Ou seja, o número 35 pode ser escrito como o produto de dois números primos (5 e 7).
Caso o número 1 também fosse Primo, seria possível escrever:
35=1.5.7;
35=1.1.5.7;
35=1.1.1.5.7;
…
Isso poderia ser feito infinitas vezes, podendo-se escrever um número composto de infinitas formas.
Em suma, pode-se definir um Número Composto como:
Todo Número Natural (N) que possui mais de dois divisores, também Naturais (N), distintos.
Exemplo:
Quais são os Números Compostos entre 1 e 10?
1) Não é primo e nem composto.
2) É primo.
3) É primo.
4) É um número composto, pois possui 3 divisores naturais (N).
5) É primo.
6) É um número composto, pois possui 4 divisores naturais (N).
7) É primo.
8) É um número composto, pois possui 4 divisores naturais (N).
9) É um número composto, pois possui 3 divisores naturais (N).
10) É um número composto, pois possui 4 divisores naturais (N).
Portanto, os números compostos entre 1 e 10 são: {4; 6; 8; 9 e 10}.
4ª Etapa: Crivo de Eratóstenes
Eratóstenes de Cirene (276 a.C. – 194 a.C.) foi um grande matemático, astrônomo, geógrafo, bibliotecário, gramático e poeta grego. Dentre suas várias contribuições, pode-se destacar um algoritmo que ele criou para se encontrar números primos até um determinado valor.
Algoritmo é um determinado conjunto de passos (comandos) que se deve executar com o objetivo de se solucionar um determinado problema, ou visando se obter um determinado resultado.
Para determinar quais números entre 1 e 100 são primos, utilizando o crivo de Eratóstenes, deve-se fazer o seguinte:
1º Passo: Crie uma tabela com todos os números de 1 a 100.
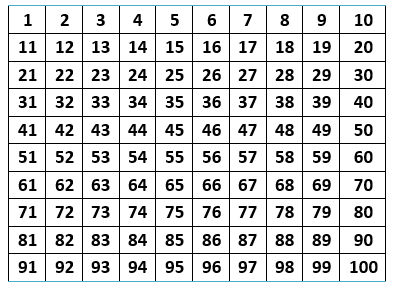
2º Passo: Elimine o número 1, pois ele não é primo e nem composto.
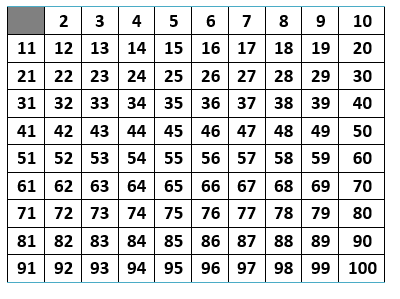
3º Passo: Encontre o primeiro número primo após o número 1, ou seja, o número 2. Elimine todos os números que são múltiplos de 2. Se eles são múltiplos de 2, não podem ser primos, pois possuem mais de dois divisores naturais (N).
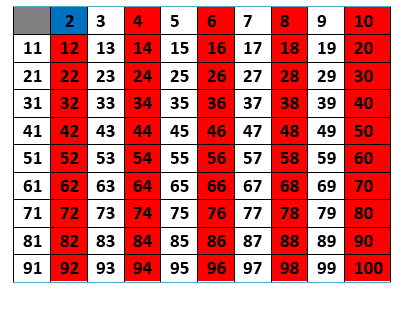 4º Passo: Em seguida, encontre o próximo número primo logo após o 2, ou seja, o número 3. Elimine todos os números que são múltiplos de 3. Se eles são múltiplos de 3, não podem ser primos, pois possuem mais de dois divisores naturais (N).
4º Passo: Em seguida, encontre o próximo número primo logo após o 2, ou seja, o número 3. Elimine todos os números que são múltiplos de 3. Se eles são múltiplos de 3, não podem ser primos, pois possuem mais de dois divisores naturais (N).
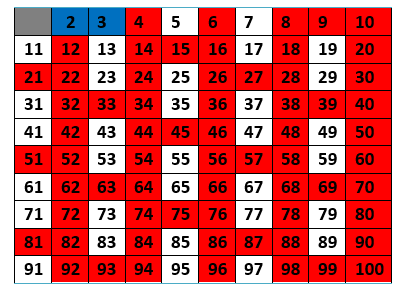 5º Passo: Agora, encontre o próximo número primo logo após o 3, ou seja, o número 5. Elimine todos os números que são múltiplos de 5. Se eles são múltiplos de 5, não podem ser primos, pois possuem mais de dois divisores naturais (N).
5º Passo: Agora, encontre o próximo número primo logo após o 3, ou seja, o número 5. Elimine todos os números que são múltiplos de 5. Se eles são múltiplos de 5, não podem ser primos, pois possuem mais de dois divisores naturais (N).
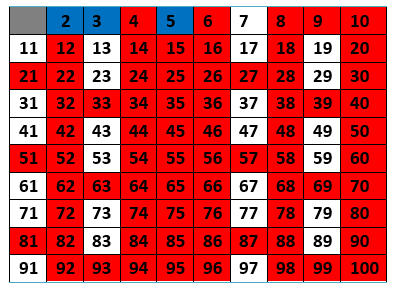
6º Passo: Finalmente, encontre o próximo número primo logo após o 5, ou seja, o número 7. Elimine todos os números que são múltiplos de 7. Se eles são múltiplos de 7, não podem ser primos, pois possuem mais de dois divisores naturais (N).
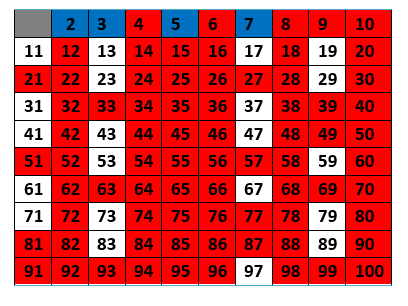 Todos os números que restaram, incluindo os números 2, 3, 5, e 7, são primos!
Todos os números que restaram, incluindo os números 2, 3, 5, e 7, são primos!
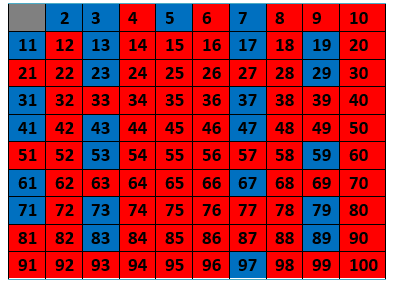
Portanto, entre 1 e 100, temos vinte e cinco números primos:
{2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47; 53; 59; 61; 67; 71; 73; 79; 83; 89; 97}
Plano de aula elaborado pelo Professor Elves Silva Moreira
Adaptação para o ensino remoto elaborada pela Prof.ª Dr.ª Nathalie Lousan
Materiais Relacionados
● Para ver conteúdos sobre Números Primos e Compostos:
Só Matemática – Números primos
Acesso em: 14 de outubro de 2020.
Números primos e compostos
Acesso em: 14 de outubro de 2020.
Descomplica – Números primos e compostos
Acesso em: 14 de outubro de 2020.
Khan Academy – Revisão de números primos e compostos
Acesso em: 14 de outubro de 2020.
Brasil Escola – O que é número composto?
Acesso em: 14 de outubro de 2020.
● Para ver vídeos sobre Números Primos e Compostos:
Números compostos e números primos – Professora Angela
Acesso em: 14 de outubro de 2020.
Números Primos e o Crivo de Eratóstenes – Vivendo a Matemática com a professora Angela
Acesso em: 14 de outubro de 2020.
O que são Números Primos? MAB#29 – Matemática Rio
Acesso em: 14 de outubro de 2020.
1 é primo? (MAT02 AULA 06) – Toda a Matemática
Acesso em: 14 de outubro de 2020.

