Conteúdos

Este plano de aula de Matemática apresenta o que é a radiciação, sua representação e principais propriedades, além da leitura de uma radiciação. Com exposição do conteúdo e exemplos, indica materiais como textos e vídeos para estudo e aprofundamento.

● Radiciação;
● Representação de uma radiciação;
● Condição de existência de radicais, e um caso especial;
● Leitura de uma radiciação;
● Propriedades da radiciação.

Objetivos

● Compreender o que é a radiciação;
● Compreender a representação de uma radiciação;
● Aprender a fazer a leitura de uma radiciação;
● Aprender as principais propriedades da radiciação.

Ensine também:

Calculando o valor de pi (π)

Números primos e números compostos

Palavras-Chave:

Radiciação. Representação de uma radiciação. Leitura de uma radiciação. Propriedades da radiciação.

Sugestão de aplicação para o ensino remoto:

As sugestões estão organizadas em tópicos com uma breve explicação de cada recurso.
● Jitsi Meet: é um sistema de código aberto e gratuito, com o objetivo de permitir a criação e implementação de soluções seguras para videoconferências via Internet, com áudio, discagem, gravação e transmissão simultânea. Possui capacidade para até 200 pessoas, não há necessidade de criar uma conta, você poderá acessar através do seu navegador ou fazer o download do aplicativo, disponível para Android e iOS.

Trabalhando com essa ferramenta, é possível:

– Compartilhar sua área de trabalho, apresentações e arquivos;
– Convidar usuários para uma videoconferência por meio de um URL simples e personalizado;
– Editar documentos simultaneamente usando Etherpad (editor de texto on-line de código aberto);
– Trocar mensagens através do bate-papo integrado;
– Visualizar automaticamente o orador ativo ou escolher manualmente o participante que deseja ver na tela;
– Reproduzir um vídeo do YouTube para todos os participantes.

● Gravação de videoaula usando o Power Point: o PPT, já tão utilizado por nós professores para preparamos nossas aulas, também permite a gravação de uma narração para os slides, que tanto nos auxiliam na explanação dos conteúdos. É possível habilitar a função de vídeo enquanto grava, assim, os alunos verão o professor em uma janelinha no canto direito da apresentação. Essa ferramenta é bem simples e eficaz. Veja um guia.

● Envio de Podcast aos alunos: podcast nada mais é do que um áudio gravado (como os enviados pelo Whatsapp). Podem ser utilizados para narrar uma história, para correção de atividades, revisar ou aprofundar os conteúdos. Para tanto, sugiro o app Anchor, que pode ser baixado no seu celular. Ele é muito fácil e simples de utilizar.

● Plataforma Google Classroom: permite a criação de uma sala de aula virtual. Essa ação irá gerar um código que será compartilhado com os alunos, para que acessem a sala. Nesse ambiente virtual, o/a professor/a poderá criar postagens de avisos, textos, slides do PPT, conteúdos, links de vídeos, roteiros de estudos, atividades, etc. É uma forma bem simples e eficaz de manter a comunicação com os alunos e postar as aulas gravadas, usando os recursos anteriormente mencionados. Confira outros recursos oferecidos pela Google, como a construção de formulários (Google Forms) para serem realizados pelos alunos.

Sugerimos aulas com até 30 minutos de duração. Além disso, nem toda aula precisa gerar uma atividade avaliativa, para não sobrecarregar os alunos. As aulas virtuais também podem ser úteis para correção de exercícios e plantões de dúvidas.

Previsão para aplicação:

5 aulas (30 min./aula).

Para a sequência didática trazida nesse plano, sugerimos o agendamento de uma aula on-line síncrona para cada uma das 5 etapas, as aulas podem ocorrer através da plataforma Jitsi Meet, organizando os conteúdos em slides e compartilhando-os com os alunos através do recurso do compartilhamento de tela do seu computador, disponível na plataforma sugerida. Ao final de cada aula, você, professor (a), pode realizar um “momento desafio”, disponibilizando 1 ou 2 exercícios aos alunos, previamente elaborados no Google formulário é disponibilizados através do Google Sala de aula. Dê alguns minutos para que realizem a atividade, e encerre a aula com sua correção e um pequeno debate dos conceitos abordados, sintetizando o conteúdo. Caso a aula síncrona não seja possível, sugiro a gravação de um vídeo com a narração dos slides através do Powerpoint e a correção dos exercícios em uma próxima aula.

1ª Etapa: O que é radiciação?

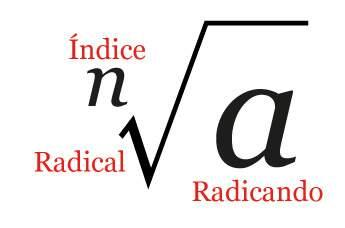
Façamos a seguinte pergunta:

1) Qual é o número que multiplicado por ele mesmo duas vezes, nos dá como resultado o número 81?
→ Resolução: Vamos representar esse número que estamos procurando pela letra “a”. Portanto, estamos procurando um número que satisfaça a seguinte operação matemática:

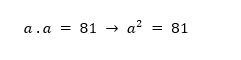
Ao reescrevermos a pergunta anterior de forma matemática, acabamos montando uma potenciação, onde “a” elevado ao quadrado é igual a 81.
Continuando a resolução do problema, temos:

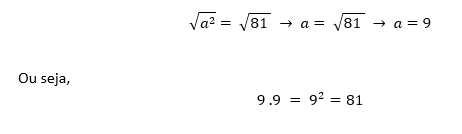
Uma outra forma de fazermos a pergunta, seria:

Qual é a raiz quadrada do número 81? Resposta: 9, pois nove vezes nove é 81.

Note que para resolvermos o problema, como foi perguntado inicialmente, precisamos montar uma potenciação. Para resolvermos a potenciação, precisamos recorrer a uma radiciação.

Naturalmente, pois, assim como as operações matemáticas básicas possuem a sua operação inversa, tal como: a subtração é a operação inversa da adição; e a divisão é a operação inversa da multiplicação; as operações matemáticas de potenciação e radiciação se relacionam da mesma forma. Ou seja, a radiciação é a operação matemática inversa da potenciação.

2ª Etapa: Representação de uma radiciação

Sempre que estivermos interessados em saber qual é a raiz de um determinado número, precisamos representar tal operação matemática da seguinte forma:

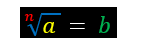
O que está escrito matematicamente logo acima, lê-se da seguinte forma: raiz enésima de ‘a’ igual a ‘b’.
Cada símbolo que aparece na representação da radiciação possui um significado importante, vejamos:

n → é o índice. É ele quem determina se estamos à procura de uma raiz quadrada, de uma raiz cúbica, etc.;
√ → esse símbolo recebe o nome de radical. É ele quem representa a operação matemática da radiciação;
a → é o radicando. O número que queremos saber a raiz enésima;
b →é a raiz. Representa o resultado da operação matemática.

Exemplo:

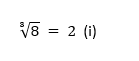
No exemplo (i), lê-se: raiz cúbica de oito igual a dois.
E temos que:

● n = 3;
● o número 8 é o radicando;
● o número 2 é a raiz.

O exemplo (i) nos diz que, se multiplicarmos o número dois três vezes seguidas por ele mesmo, obtemos como resultado o número oito. Matematicamente:

Mais uma vez, percebemos o quão intimamente relacionadas estão as operações matemáticas de radiciação e potenciação.

3ª Etapa: Condição de existência de radicais (e um caso especial)

Para que a operação matemática de radiciação exista (no conjunto dos números reais ℝ), é preciso estarmos atentos aos valores que o índice “n” e o radicando “a” assumem.
Existem alguns casos que merecem a nossa atenção. Vejamos:

● Para o caso em que o índice “n” é par (n ∈ N) e o radicando “a” é negativo (a < 0), não existem raízes reais.

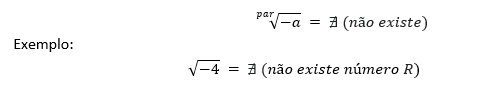
● Para o caso em que o índice “n” é par (n ∈ N) e o radicando “a” é positivo (a > 0), existem duas raízes simétricas.

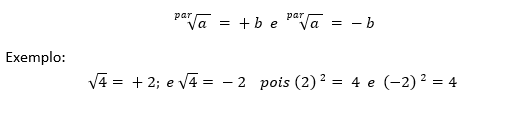
● Para o caso em que o índice “n” é ímpar (n ∈ N) e o radicando “a” é negativo (a < 0), existe uma única raiz negativa.

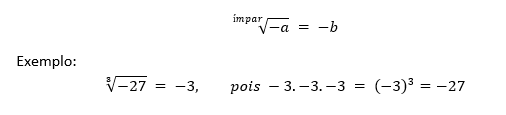
● Para o caso em que o índice “n” é ímpar (n ∈ N) e o radicando “a” é positivo (a > 0), existe uma única raiz positiva.

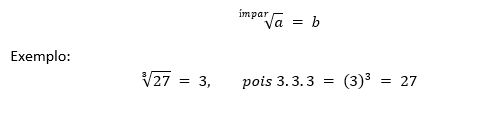
● Para o caso que o índice “n” é ímpar ou par (n ∈ N), e o radicando “a” é nulo (a = 0), existe uma única raiz, que será sempre zero (0).

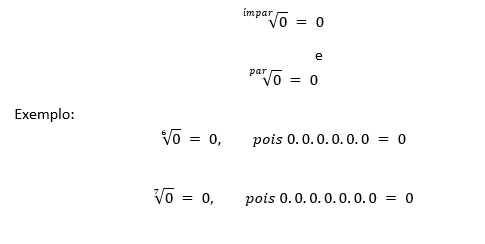
4ª Etapa: Leitura de uma radiciação

O índice “n” determina qual é a raiz que estamos procurando.
Para cada valor de “n” temos uma certa leitura. Vejamos:

● Para n = 2, lê-se “raiz quadrada”. Para este índice, convencionou-se que ele não precisa ser representado. Ou seja, sempre que encontrarmos um radical “√” sem índice, podemos assumir que se trata de uma raiz quadrada.
Exemplos:

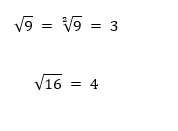
● Para n = 3, lê-se “raiz cúbica”.
Exemplos:

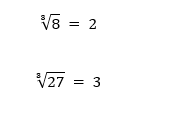
● Para n = 4, lê-se “raiz quarta”.
Exemplos:

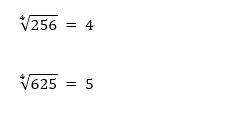
● Para n = 5, lê-se “raiz quinta”.
Exemplos:

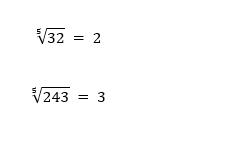
E assim segue para n = 6, 7, 8, 9, 10, …, n ∈ N.

● Para o caso geral, n = n, lê-se “raiz enésima”.
Exemplo:

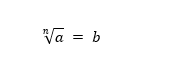
5ª Etapa: Propriedades da radiciação

Assim como as demais operações matemáticas possuem as suas próprias regras e propriedades, a radiciação também possui as suas. Vejamos:

● (I) Radicais de mesmo índice
→ A raiz enésima do produto é igual ao produto das raízes enésimas:

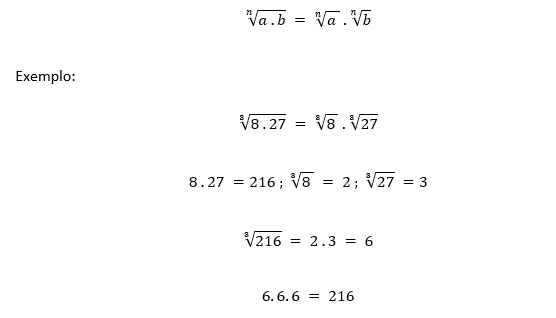
→ A raiz enésima da razão é igual a razão das raízes enésimas:

● (II) Raiz de raiz
→ Para se calcular a raiz de uma raiz, basta repetir o radicando “a” e um símbolo de radical “√”, e multiplicar os índices “n” e “m”:

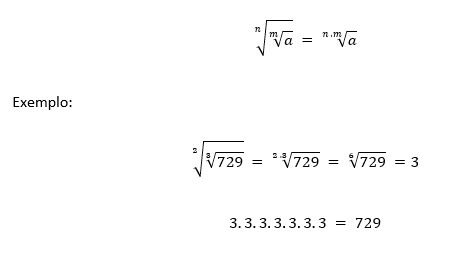
● (III) Raiz de potência
→Calcular a raiz e depois a potência é equivalente (igual) a calcular a potência e depois a raiz:

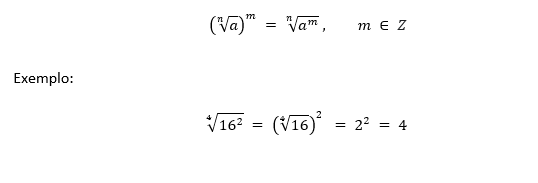● (IV) Alteração do índice
→Dividir e multiplicar o índice (n) do radical “√” e o expoente (m) do radicando “a” pelo mesmo número não altera o resultado:

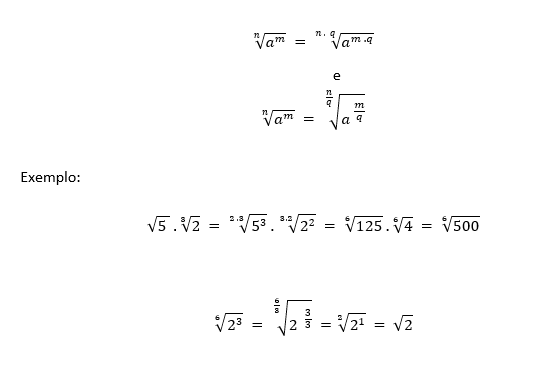
● (V) A raiz enésima de um radicando elevado a “n”
→Neste caso, o resultado é igual ao próprio radicando:

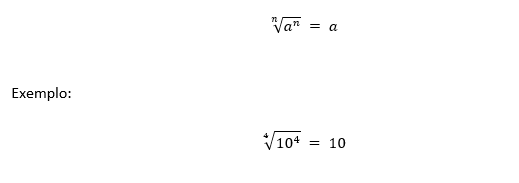
● (VI) Potência de expoente racional
→Como já vimos, a potenciação é a operação matemática inversa da radiciação. Desta forma, sempre que tivermos uma potência podemos reescrevê-la na forma de radical (radiciação). E sempre que tivermos um radical (radiciação) podemos reescrevê-lo na forma de potência. Para tal, o índice (n) do radical “√” corresponde ao denominador, e o expoente (m) do radicando “a” corresponde ao numerador do expoente:

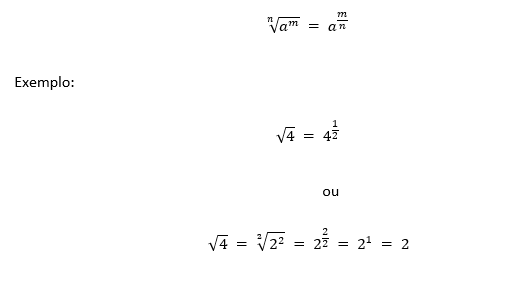
Plano de aula elaborado pelo Professor Elves Silva Moreira
Adaptação para o ensino remoto elaborada pela Prof.ª Dr.ª Nathalie Lousan

Materiais Relacionados

● Para ver conteúdos sobre radiciação:

Livro em PDF (p. 59-67)
Acesso em: 30 de janeiro de 2021.

Radiciação – Mundo Educação
Acesso em: 30 de janeiro de 2021.

Matemática Básica
Acesso em: 30 de janeiro de 2021.

Brasil Escola
Acesso em: 30 de janeiro de 2021.

Educa mais Brasil
Acesso em: 30 de janeiro de 2021.

Toda Matéria
Acesso em: 30 de janeiro de 2021.

O que é radiciação?
Acesso em: 30 de janeiro de 2021.

Central Exatas
Acesso em: 30 de janeiro de 2021.

Info Escola
Acesso em: 30 de janeiro de 2021.

● Para ver vídeos sobre radiciação:

Radiciação – Brasil Escola
Acesso em: 30 de janeiro de 2021.

Radiciação – definições
Acesso em: 30 de janeiro de 2021.

Tags relacionadas