Conteúdos
Este plano de aula apresenta dois sistemas de numeração: o decimal e o binário. Inicialmente, faz-se uma discussão introdutória sobre a necessidade de criar uma linguagem específica para comunicar comandos “inteligíveis” a uma máquina. Em seguida, faz-se uma brevíssima revisão do sistema de numeração decimal. Na etapa seguinte, apresenta-se o sistema de numeração binário, chamando a atenção para as potências de base 2, discutindo exemplos de como escrever um número decimal no sistema binário. A última etapa consiste no processo inverso, ou seja, trata de como passar um número escrito no sistema binário para o sistema decimal.
● Sistema de numeração decimal;
● Sistema de numeração binário; e
● Reescrevendo um número do sistema binário para o decimal.
Objetivos
● Compreender a diferença entre o sistema de numeração decimal e o binário;
● Compreender a diferença entre um bit e um Byte; e
● Aprender a reescrever um número escrito no sistema decimal no sistema binário, e vice-versa.
Ensine também:
Introdução à geometria analítica
Matemática financeira: juros compostos
Palavras-chave:
Sistema de numeração decimal. Sistema de numeração binário. Bits. Bytes. Computação.
Previsão para aplicação:
4 aulas (50 min./aula)
1ª Etapa: Introdução
Nós, seres humanos, somos capazes de identificar os mais diversos tipos de símbolos, letras, números, sons, cores etc. Portanto, para dois indivíduos da mesma espécie (humana) trocarem informações, basta que ambos dominem o mesmo idioma (a mesma linguagem).
Contudo, para comunicar-se com uma máquina (um computador, por exemplo), faz-se necessário um novo tipo de linguagem, pois, diferente dos seres humanos, tais máquinas não são capazes de reconhecer muitos tipos de símbolos. Uma linguagem construída para comunicar comandos para um computador é dita linguagem computacional.
Basicamente, uma máquina só é capaz de identificar dois tipos de símbolos, que são, na realidade, impulsos elétricos, e podem ser identificados como: verdadeiro ou falso, ligado ou desligado, sim ou não e 0 ou 1. Tais símbolos representam a presença, ou a ausência, de corrente elétrica. Por questões de simplificação, habitualmente utiliza-se os 0s e os 1s, quando se trata de uma linguagem computacional.
Por se tratar de uma linguagem que possui apenas dois símbolos, 0 e 1, esse tipo de linguagem é caracterizada como binária.
No universo da informática e da computação, uma palavra muito comum é o termo ‘bit’. Tal palavra tem origem no idioma inglês, sendo uma contração da expressão “bynary digit”, que pode ser traduzida livremente para “dígito binário”. Outro termo bastante comum é o ‘Byte’, que possui a seguinte relação com o bit:
1 Byte=8 bits
Usualmente, o bit, que costuma ser representado pela letra ‘b’ (minúscula) é utilizado para mensurar a capacidade de transferência, ou de armazenamento, de informação digital.
Cada bit pode assumir apenas dois valores: 0 ou 1. No entanto, cada Byte, frequentemente representado pela letra ‘B’ (maiúscula), pode assumir oito valores de 0s e 1s.
2ª Etapa: Sistema de numeração decimal
O sistema de numeração decimal trabalha com 10 símbolos (por isso chama-se decimal), que são os algarismos indo-arábicos:
0,1,2,3,4,5,6,7,8,9
Por maior que seja o número que a nossa mente possa imaginar, a partir desses 10 símbolos somos capazes de representar todo e qualquer número.
O sistema de numeração decimal é essencialmente posicional, ou seja, o valor que cada algarismo possui depende da posição (casa) que ele ocupa na representação de um determinado número.
Vejamos a tabela a seguir:
O número representado na Tabela 1 é “setecentos e onze mil, seiscentos e noventa e três”.
Esse número pode ser decomposto, da seguinte forma:
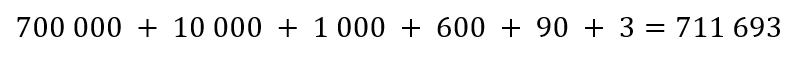
Pode-se reescrevê-lo, também, como uma soma de potências de base 10:
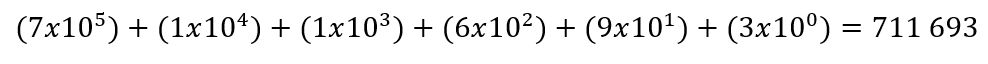
Como o sistema de numeração decimal é posicional e, quanto mais à esquerda um algarismo estiver, maior o seu valor numérico, as potências de 10, naturalmente, aparecem em ordem decrescente.
Na Tabela 1, se trocarmos o algarismo que está na casa das centenas de milhar (7) com o algarismo que está na casa das dezenas (9), teremos um novo número:
O número representado na Tabela 2 é “novecentos e onze mil, seiscentos e setenta e três”. Tal troca dos algarismos, da casa das centenas de milhar com o algarismo das dezenas, evidencia o caráter posicional do sistema de numeração decimal.
Do mesmo modo como foi feito com o número representado na Tabela 1, pode-se representar o número da Tabela 2 da seguinte maneira:
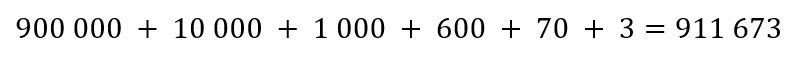
E, de forma análoga, ele também pode ser expresso como uma soma de potências de base 10:
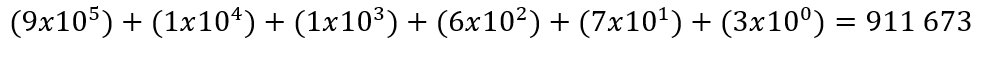
De fato, todo e qualquer número natural pode ser expresso como uma soma de potências de base 10.
Com o objetivo de facilitar a consulta de algumas potências de base 10, segue-se:
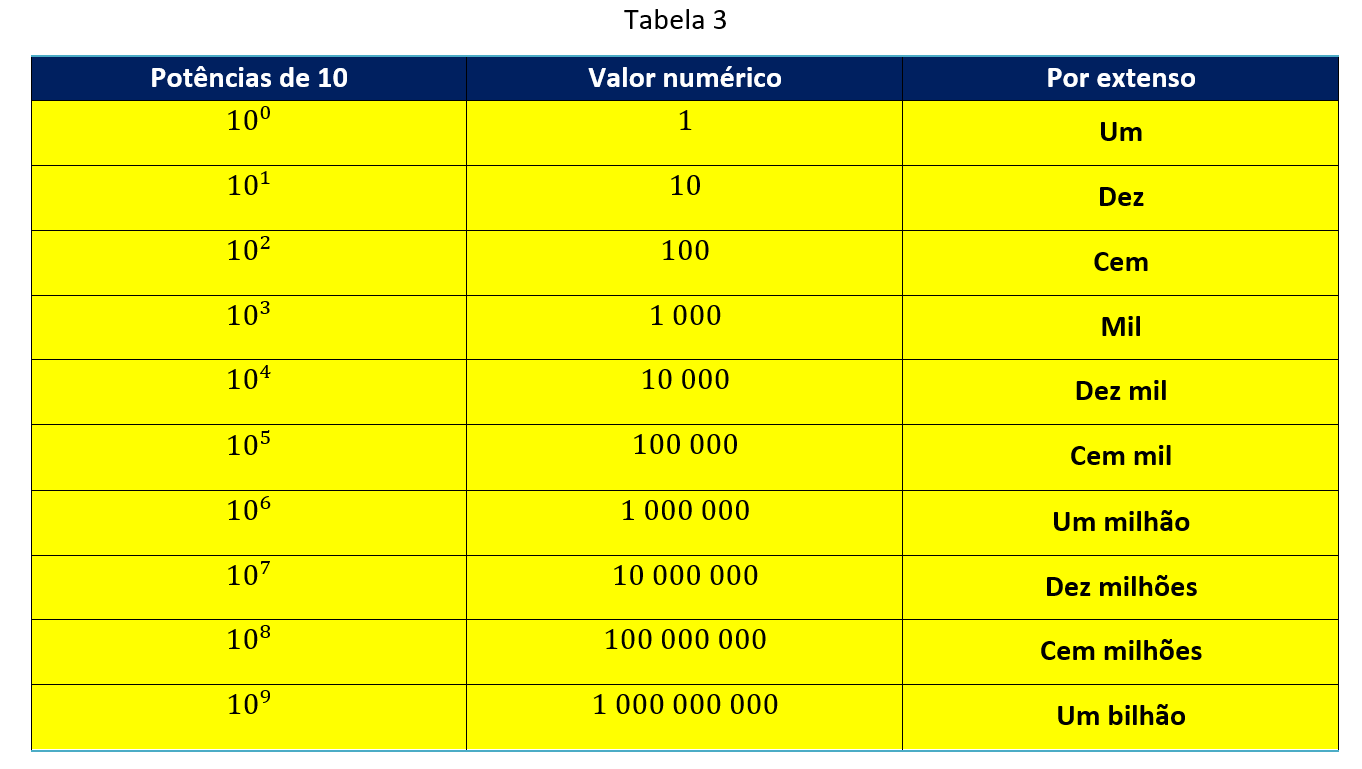
3ª Etapa: Sistema de numeração binário
No sistema de numeração binário, utiliza-se apenas dois símbolos: 0 ou 1 (os bits).
Por questões de praticidade, nesse sistema de numeração é mais conveniente trabalhar com potências de base 2. Por esse motivo, a Tabela 4 nos traz algumas potências de base 2:
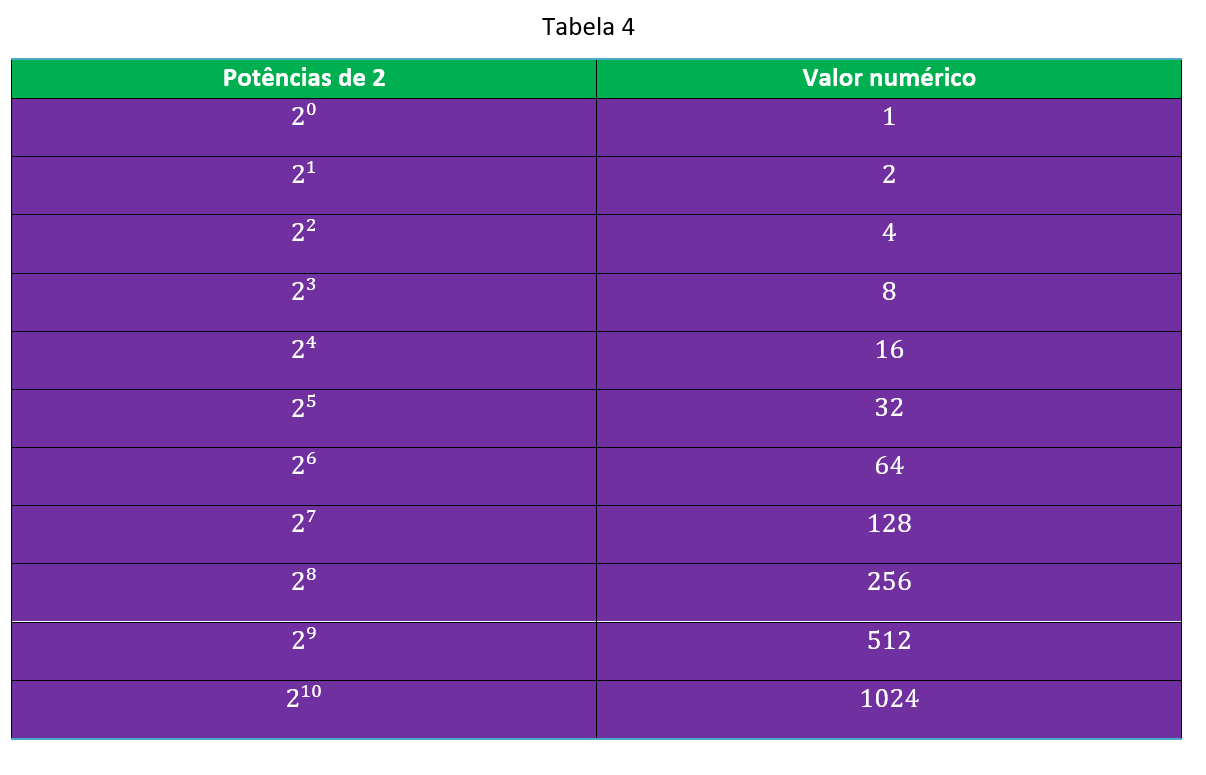
Na etapa anterior, vimos que é possível representar qualquer número natural a partir da soma de potências de base 10, em que as potências aparecem em ordem decrescente (da maior para a menor), e cada uma das potências é multiplicada por um dos 10 algarismos do sistema de numeração decimal (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Agora, faremos algo semelhante: iremos representar alguns números naturais a partir da soma de potências de base 2, em que as potências também aparecerão em ordem decrescente. Contudo, as potências de base 2 serão multiplicadas por apenas dois algarismos, 0 ou 1. Vejamos:
Exemplo 1 – Representação do número 29 no sistema de numeração binário:
O número 29 pode ser escrito como:
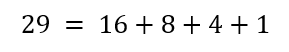
Reescrevendo-o como uma soma de potências de base 2, temos:
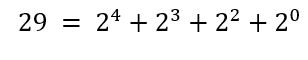
Para se representar um número natural no sistema de numeração binário, todas as potências de base 2 devem ser consideradas. Por esse motivo, iremos reescrever o número 29 da seguinte forma:
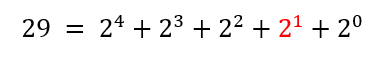
Desta forma, temos que o número 29 pode ser expresso como:
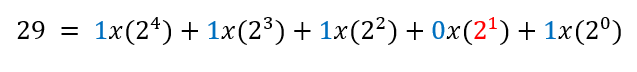
Para indicar que um número está sendo expresso no sistema decimal, utiliza-se o número 10 subscrito. E, para indicar que um determinado número está sendo expresso no sistema binário, utiliza-se o número 2 subscrito. Portanto, tem-se que a representação decimal e binária do número 29 é:
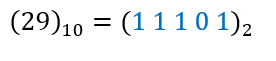
Exemplo 2 – Representação do número 26 no sistema de numeração binário:
O número 26 pode ser escrito como:
Reescrevendo-o como uma soma de potências de base 2, temos:
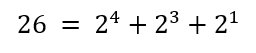
Escrevendo todas as potências de base 2 necessárias para que a ordem decrescente das potências esteja completa, temos:
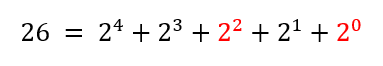
Desta forma, temos que o número 26 pode ser expresso como:
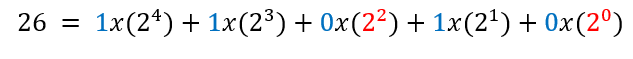
Portanto, tem-se que a representação decimal e binária do número 26 é:
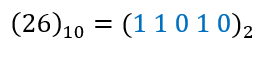
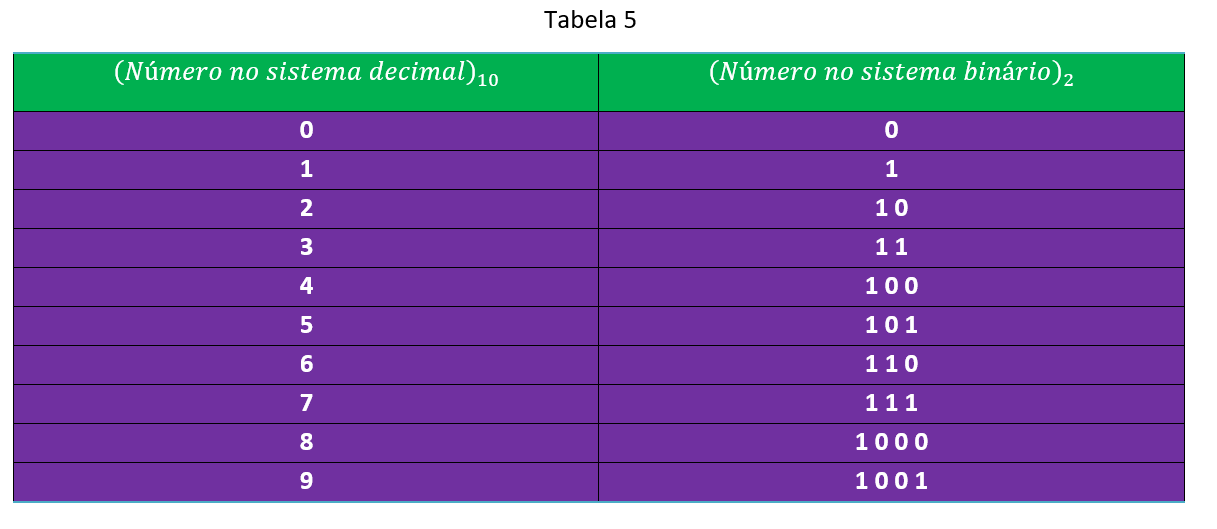
Agora, vamos escrever os algarismos que são utilizados no sistema decimal (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), no sistema binário:
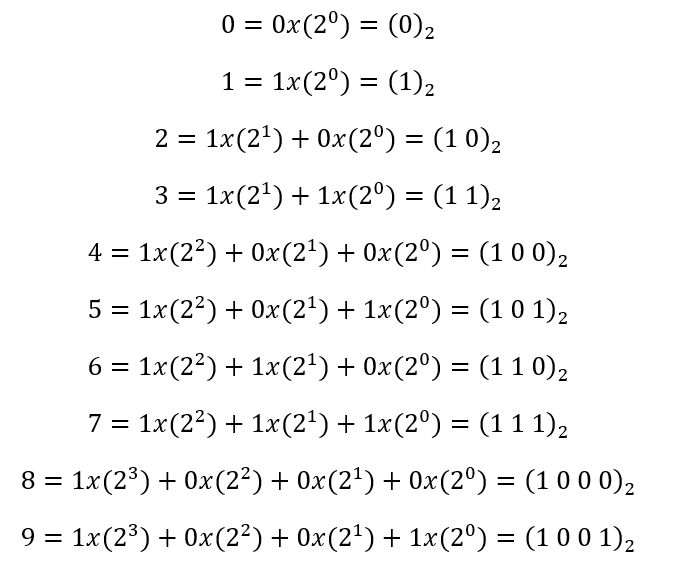
O que pode ser organizado da seguinte forma:
4ª Etapa: Reescrevendo um número do sistema binário para o decimal
Nesta etapa, faremos o processo inverso da etapa anterior. Vamos pegar um número escrito no sistema de numeração binário e transformá-lo (reescrevê-lo) para o sistema de numeração decimal.
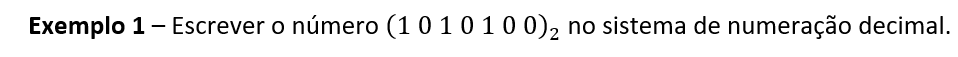
Como esse número possui sete bits (sete 0s e 1s), vamos começar escrevendo a soma das sete primeiras potências de base 2, em ordem decrescente, deixando um espaço na frente de cada uma das potências, para posteriormente as multiplicarmos pelos bits 0 ou 1 correspondentes:
Esse número também possui sete bits, logo, o processo é bastante semelhante ao do exemplo anterior:
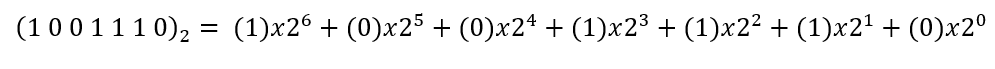
Consultando a Tabela 4 mais uma vez, temos:
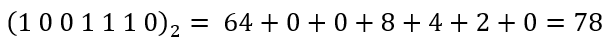
Ou seja,
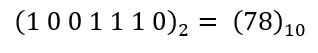
Plano de aula elaborado pelo Professor Elves Silva Moreira
Coordenação Pedagógica: Prof.ª Dr.ª Aline Monge
Materiais Relacionados
● Para ver conteúdos sobre a matemática dos bits e Bytes, sistema decimal e binário:
Brasil Escola
Acesso em: 02 de outubro de 2021.
Infowester
Acesso em: 02 de outubro de 2021.
Tecnoblog
Acesso em: 02 de outubro de 2021.
Click Idea
Acesso em: 02 de outubro de 2021.
Calculadora binária
Acesso em: 02 de outubro de 2021.
● Para ver vídeos sobre a matemática dos bits e Bytes, sistema decimal e binário:
Brasil Escola
Acesso em: 02 de outubro de 2021.
M3 Matemática Multimídia
Acesso em: 02 de outubro de 2021.
Canaltech
Acesso em: 02 de outubro de 2021.
Marcos Aba Matemática
Acesso em: 02 de outubro de 2021.
Dicionário de Informática
Acesso em: 02 de outubro de 2021.