Conteúdos
– Geometria analítica
– Plano cartesiano
Objetivos
– Compreender as ideias relacionadas à geometria analítica
– Conhecer e trabalhar com plano cartesiano
– Calcular distância entre dois pontos
– Encontrar ponto médio de segmento
Previsão para aplicação:
4 aulas (50 min/aula)
1ª Etapa: Geometria analítica - plano cartesiano
A geometria analítica, cuja criação é atribuída ao filósofo francês Rene Descartes na década de 1630, é a parte da matemática que estuda os entes geométricos por meio de um sistema de coordenadas e por meio da álgebra. Esta relação permite resolver problemas geométricos por meio da álgebra e vice-versa, e tem muitas aplicações na física e na engenharia. Este conteúdo geralmente é abordado no terceiro ano do ensino médio.
Para iniciar o tema, explique para os alunos que a geometria analítica estuda entes geométricos, tais como ponto, reta e círculo, posicionados em um sistema de coordenadas, que é chamado de plano cartesiano. O primeiro passo, portanto, é conhecer o plano cartesiano:
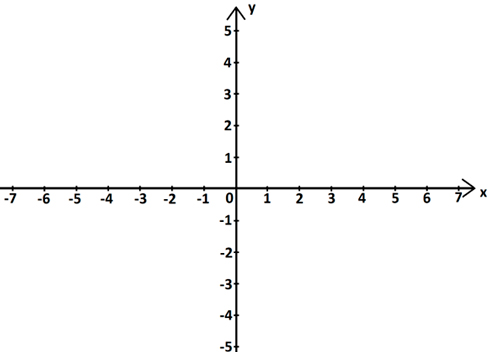
Ele é formado por um par de retas perpendiculares que se encontram em um ponto chamado origem. A partir da origem, as coordenadas no eixo horizontal (eixo x) crescem da esquerda para direita, e as coordenadas no eixo vertical (eixo y) crescem de cima para baixo, como mostrado na figura acima.
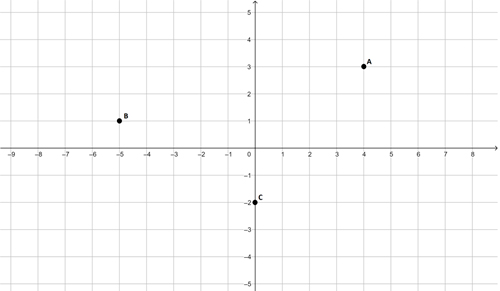
O plano cartesiano, assim como outros sistemas de coordenadas, serve para posicionar objetos através de um par de coordenadas. Quando vamos posicionar um ponto no plano cartesiano, usamos um par de números colocados entre parênteses. Faça alguns exemplos na lousa, por exemplo, os dos pontos colocados no plano cartesiano abaixo. O ponto A tem coordenadas (4,3); o ponto B tem coordenadas (-5, 1) e o ponto C (0, -2). Note que a coordenada referente ao eixo x sempre vem na frente.
Mostre aos alunos outras situações onde é utilizado algum sistema de coordenadas. Por exemplo, o tabuleiro de xadrez, para posicionar as peças usa coordenadas que envolvem letras e números.
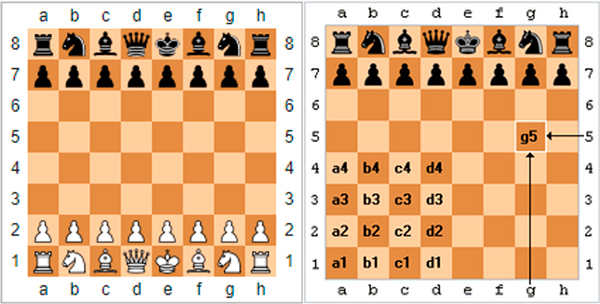
Um diagrama de xadrez mostrando todas as peças e peões em suas casas iniciais. A casa g5 identificada no tabuleiro de xadrez por meio do sistema algébrico
Fonte: Xadrez – Wikipedia
Outro grande exemplo são as coordenadas geográficas latitude e longitude, que são utilizadas para encontrar posições no globo terrestre. Estas coordenadas podem ser vistas no mapa abaixo. As linhas horizontais são latitudes e as linhas verticais são longitudes.
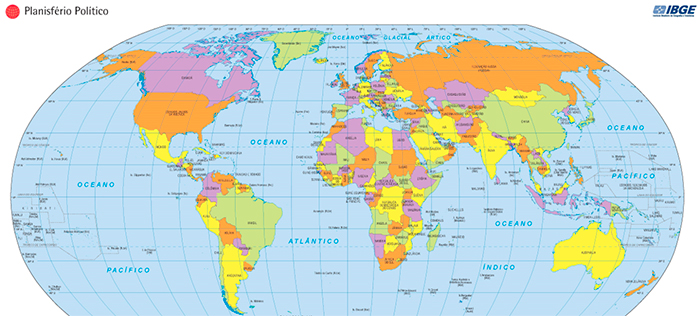
Fonte: Mapas – IBGE
Para finalizar, peça para os alunos desenharem um plano cartesiano no caderno e posicionar alguns pontos, como por exemplo: (5, 6); (-2, 0); (-7, -3); (0, 4); (0, 0).
2ª Etapa: Geometria analítica – distância entre pontos
Na segunda etapa o objetivo é que os estudantes compreendam como encontrar a distância entre dois pontos a partir de suas coordenadas cartesianas. A princípio, desenhe na lousa um plano cartesiano como o que segue abaixo e discuta com eles como pode ser calculada a distância entre os pontos A e B.
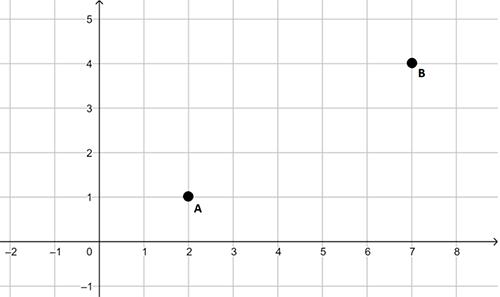
A intenção é que percebam a necessidade de utilizar o Teorema de Pitágoras. A partir daí procure deduzir junto com a turma uma fórmula para calcular a distância entre dois pontos utilizando suas coordenadas. A distância D entre os pontos A (xa, ya) e B (xb,yb) é:
D=√(xb-xa)2+(yb-ya)2
Em seguida, passe alguns exercícios para que os alunos possam praticar. Seguem algumas possibilidades:
1) Calcule a distância entre os pontos A (4, 2) e B (3, 3).
2) Calcule a distância entre os pontos A (-7, -1) e B (1, 4).
3) Calcule a distância entre os pontos A (-5, 2) e B (3, -7).
4) Calcule a distância entre os pontos A (-3, -6) e B (-2, 5).
Os pontos devem ser posicionados no plano cartesiano desenhado no caderno. Pode-se utilizar aproximações e calculadora para resolver.
Para trabalhar com a próxima tarefa será necessário imprimir a figura abaixo para entregar aos estudantes. Se achar conveniente, organize a turma em duplas. Seguem as questões que também devem ser entregues aos alunos ou escritas na lousa:
1) No mapa abaixo posicione os seguintes pontos:
a) A (4, -4)
b) B (2, 2)
c) C (0, -2)
d) D (6, 3)
e) E (2, 0)
2) Em qual estado da federação brasileira estão posicionados cada um dos pontos da questão anterior?
3) Encontre um ponto que esteja posicionado dentro de cada um dos seguintes estados:
a) Minas Gerais
b) Maranhão
c) São Paulo
d) Rio de Janeiro
4) Calcule as seguintes distâncias:
a) distância entre os pontos A e B da questão 1.
b) distância entre os pontos C e E da questão 1.
c) distância entre os pontos A e D da questão 1.
Para que os alunos encontrem o nome dos estados, pode-se permitir pesquisa na Internet. Para a questão 4 pode-se utilizar calculadora. Observe que para encontrar pontos dentro do Rio de Janeiro, será necessário utilizar coordenadas decimais.
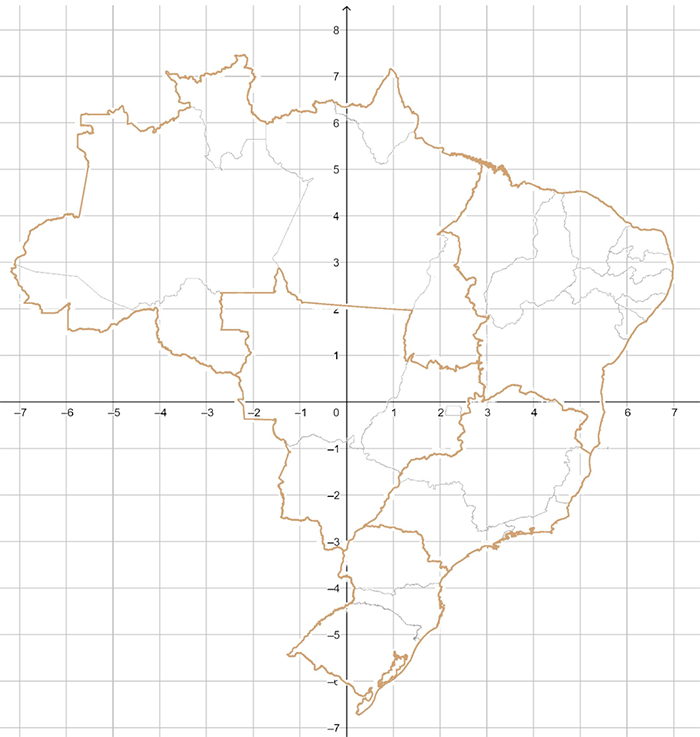
Confira a imagem acima em tamanho maior
Fonte: IBGE e elaboração do autor.
Após finalizada a tarefa, discuta com a turma os resultados encontrados.
Materiais Relacionados
1) Para ver o conteúdo de geometria analítica:
René Descartes – Wikipedia. Acesso em: 01 de dezembro de 2019.
Geometria analítica – Mundo Educação. Acesso em: 01 de dezembro de 2019.
2) Para acessar mapas do IBGE. Acesso em: 01 de dezembro de 2019.
3) Para ver o conteúdo em livro didático:
BIGODE, Antônio José Lopes. Matemática no Cotidiano. Editora Scipione, 2015.