Conteúdos
Neste roteiro de estudos você irá estudar sobre as posições relativas entre duas circunferências, retas e circunferências, e pontos e circunferências.
O estudo das posições relativas entre retas e circunferências envolve análise algébrica e geométrica, fornecendo ferramentas importantes para resolver problemas práticos em diversas áreas, como física, engenharia e computação.
Objetivos
- Identificar a posição relativa entre duas circunferências;
- Identificar a posição entre uma reta e uma circunferência; e
- Identificar a posição entre um ponto e uma circunferência.
Conteúdos / Objetos do conhecimento:
- Posição relativa entre circunferências
Palavras-chave:
Reta. Circunferência. Ponto. Posição relativa.
Proposta de trabalho:
A proposta é desenvolvida para que você, estudante, possa realizar os estudos em qualquer ambiente. O material está dividido em duas etapas, de forma que, na primeira, você estudará sobre a equação geral da reta, e na segunda etapa você irá estudar sobre a equação reduzida da reta, para então finalizar com alguns exercícios de aplicação.
1ª Etapa: Posição relativa entre ponto e circunferência
Dentro da geometria analítica, podemos analisar a posição relativa entre um ponto e uma circunferência a partir de sua equação e as coordenadas do ponto P(x,y). Vamos lá:
1° Caso – quando o ponto é exterior à circunferência. Veja:
Se um ponto P(x,y) é exterior à circunferência de centro C(a,b), podemos dizer que a distância entre o ponto e o centro da circunferência é maior do que o raio:
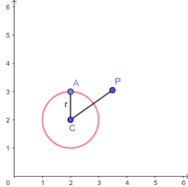
Se pensarmos na equação da circunferência, podemos fazer o seguinte:
![]()
2° Caso – quando o ponto é interior a circunferência. Veja:
Se um ponto P(x,y) é interior à circunferência de centro C(a,b), podemos dizer que a distância entre o ponto e o centro da circunferência é menor do que o raio:
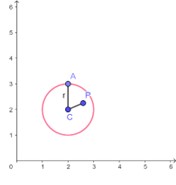
Se pensarmos na equação da circunferência, podemos fazer o seguinte:
![]()
3° Caso – quando o ponto pertence à circunferência. Veja:
Se um ponto P(x,y) pertence à circunferência de centro C(a,b), podemos dizer que a distância entre o ponto e o centro da circunferência é igual ao raio:
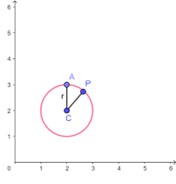
Se pensarmos na equação da circunferência, podemos fazer o seguinte:
Verifique a posição do ponto P (2,3) em relação à circunferência
Resolução: Neste caso, basta substituir as coordenadas do ponto:
Assim
Portanto, o ponto é externo à circunferência, uma vez que a distância é maior do que a medida do raio.
2ª Etapa: Posição relativa entre reta e circunferências
Agora, pense um pouco: como você faria para determinar a distância entre uma reta e uma circunferência?
Basta, calcular a distância entre o centro C(a,b) e a reta. Temos três casos, veja:
Considere a reta de equação geral Ax+By+C=0 e a circunferência de equação
![]()
1º Caso: Reta secante à circunferência
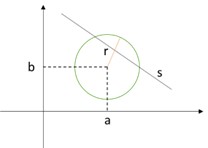
Neste caso, a distância entre a reta e o centro é menor do que a medida do raio:
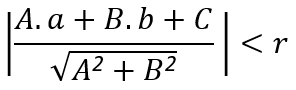
2º Caso: Reta exterior
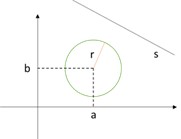
Neste caso, a distância entre a reta e o centro é maior do que a medida do raio:
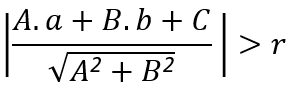
3º Caso: Reta tangente:
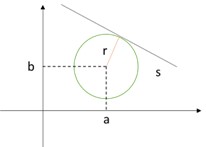
Neste caso, a distância entre a reta e o centro é igual à medida do raio:
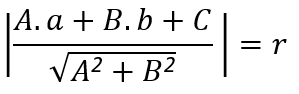
Verifique se compreendeu:
Qual é a posição da reta r, dada pela equação em relação à circunferência de equação ?
Resolução:
Neste caso, precisamos encontrar o centro da circunferência:

Percebe-se que a distância é menor do que a medida do raio, portanto a reta é secante.
3ª Etapa: Posição relativa entre circunferências
Agora, pense um pouco sobre as posições relativas entre as duas circunferências. Será que são semelhantes às posições tratadas acima? Em seguida, assista ao vídeo a seguir:
“G. A. Posição relativa entre circunferências”
Acesso em: 24 de janeiro de 2024.
4ª Etapa: Praticando
1) Qual é a posição do ponto 𝑃 em relação à circunferência 𝜆 em cada caso?
a) P(1,2) e 𝜆:
b) 𝑃(1,5) e 𝜆:
c) 𝑃(4, −2) e 𝜆:
Gabarito:
a) Interior.
b) Exterior.
c) Sobre a circunferência
Crédito: Brainly
2) Qual é a posição da reta 𝑠 em relação à circunferência 𝜆 em cada um dos casos a seguir?
a) 𝑠: 3𝑥 − 4𝑦 + 15 = 0 e 𝜆:
b) 𝑠: 2𝑥 − 𝑦 + 1 = 0 e 𝜆:
c) 𝑠: 4𝑥 + 3𝑦 + 8 = 0 e 𝜆:
Gabarito
a) Tangente.
b) Secante.
c) Exterior
Crédito: Brainly
Materiais Relacionados
Para te ajudar a complementar os estudos, você pode acessar:
“G. A. Posição relativa entre circunferências”
Acesso em: 24 de janeiro de 2024.
“G. A. Posição relativa entre reta e circunferência”
Acesso em: 24 de janeiro de 2024.
Acesso em: 24 de janeiro de 2024.
Roteiro de estudos elaborado pelo professor Cícero Inacio dos Santos.
Revisão textual: professora Daniela Leite Nunes.
Coordenação Pedagógica: prof. dr.ª Aline Bitencourt Monge.
Crédito da imagem: Karolina Grabowska – Pexels




