Conteúdos
Este roteiro de estudos de Matemática apresenta, de forma introdutória, o conceito de permutação, tanto simples quanto com repetição. O material inicia fazendo uma breve discussão quanto ao significado da palavra “permuta”, mencionando a importância de tal significado para o estudo da análise combinatória. Posteriormente, sugere-se a leitura de um texto, para maior aprofundamento sobre a permutação simples, com a apresentação de algumas questões. Logo em seguida, o mesmo caminho é percorrido em relação à permutação com repetição, sendo que, após a indicação de leitura de um texto sobre o assunto, algumas questões são expostas. O material também conta com algumas indicações de vídeos (possibilitando ampliação e aprofundamento em determinados tópicos). Ao final, encontram-se alguns exercícios resolvidos.
● Introdução;
● Permutação simples;
● Permutação com repetição; e
● Cheque seus conhecimentos.
Objetivos
● Aprender o que é uma permutação simples;
● Aprender o que é uma permutação com repetição; e
● Compreender a representação matemática para uma permutação (tanto simples quanto com repetição).
Palavras-chave:
Permutação simples. Permutação com repetição. Fatorial de um número natural.
Proposta de trabalho:
O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.
Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.
1ª Etapa: Introdução
Nos primórdios das mais diversas civilizações, antes da invenção do dinheiro, quando uma pessoa queria adquirir um bem ou produto produzido por outras pessoas, geralmente, fazia-se trocas.
Por exemplo:
Imaginemos que uma determinada pessoa fosse produtora de milho, enquanto outra pessoa era produtora de tecidos (roupas). Se fosse do interesse de ambas as partes, poderia criar-se uma convenção de equivalência entre os dois produtos (milho e tecido), tal como: um saco de milho poderia ser trocado por duas peças de tecidos (como duas camisas). Ao efetuarem esse tipo de troca entre produtos distintos, os nossos antepassados estavam realizando aquilo que chamamos de permuta.
Em Matemática, ao estudarmos diversos conceitos de análise combinatória, a troca de posição de elementos de um determinado conjunto revela-se bastante importante. Dessa forma, surge o conceito de permutação simples, que pode ser considerado um caso particular de arranjo.
A permutação simples consiste na troca de posição de n elementos de um determinado conjunto, em que todos os elementos são distintos (ou seja, não existem elementos repetidos), gerando diferentes formas de se organizar os elementos, isto é, formando distintas combinações entre os n elementos do conjunto em questão. Para o caso da troca de posição de n elementos de um determinado conjunto, em que k elementos desse mesmo conjunto se repetem, temos, naturalmente, a permutação com repetição.
A seguir, veremos como calcular o número de combinações possíveis em ambos os casos: permutação simples e permutação com repetição.
2ª Etapa: Permutação simples
Pergunta norteadora: o que é uma permutação simples?
OLIVEIRA, Raul Rodrigues de. “Permutação simples”; Brasil Escola.
Acesso em: 28 de maio de 2022.
A partir da leitura da etapa “Introdução” deste material, bem como do texto acima, responda às seguintes perguntas:
1 – A permutação simples é um dos casos de agrupamento estudado em qual área da Matemática?
2 – Como se chama a permutação de n elementos de um conjunto, em que todos os elementos são distintos?
3 – Como se chama a permutação de n elementos de um conjunto, em que k elementos do conjunto são repetidos?
4 – Como se lê o símbolo: “n!”?
5 – Como se calcula o número de combinações possíveis em uma permutação simples?
6 – Quanto vale P9 ?
7 – Como se chamam todas as reordenações possíveis das letras que formam uma determinada palavra?
Respostas às perguntas da 2ª Etapa:
1 – Permutação simples (e com repetição) é estudada em análise combinatória.
2 – Uma permutação que envolve elementos distintos entre si é uma permutação simples.
3 – Uma permutação que envolve elementos repetidos é, naturalmente, uma permutação com repetição.
4 – n! → lê-se n fatorial.
5 – A expressão matemática para o cálculo do número de combinações possíveis de n elementos de um determinado conjunto, em uma permutação simples é: Pn = n!
6 –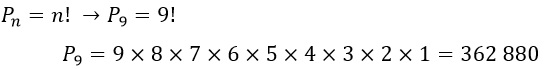
Assim, um conjunto formado por 9 elementos distintos pode ser organizado (combinado) de 362 880 maneiras diferentes!
7 – Chamam-se ANAGRAMAS.
Para saber mais, assista:
Permutação simples – Toda a Matemática
Acesso em: 28 de maio de 2022.
Permutação simples – Equaciona Com Paulo Pereira
Acesso em: 28 de maio de 2022.
3ª Etapa: Permutação com repetição
Pergunta norteadora: o que é uma permutação com repetição?
RAMOS, Danielle de Miranda. “Permutação com elementos repetidos “; Brasil Escola.
Acesso em: 28 de maio de 2022.
A partir da leitura do texto acima, responda às seguintes perguntas:
1 – Qual expressão matemática utilizamos para calcular o número de combinações possíveis em uma permutação com n elementos, em que n1, n2 e n3 elementos estão repetidos?
2 – Quantos anagramas podem ser formados pela palavra OVO?
3 – Quantos anagramas podem ser formados pela palavra BOLO?
Respostas das perguntas da 3ª Etapa:
1 – Para uma permutação com tal repetição, utilizamos:
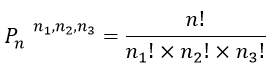
2 – A palavra “OVO” tem 3 elementos (3 letras). No entanto, dois deles, a letra “O” aparece de forma repetida. Assim, calculamos:
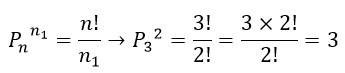
3 – A palavra “BOLO” possui 4 elementos (4 letras). Contudo, novamente, a letra “O” aparece duas vezes. O cálculo deve ser, então:
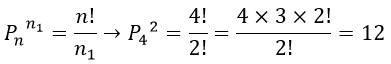
Dessa forma, com a palavra “BOLO” podemos formar 12 anagramas distintos.
Para saber mais, assista:
Permutação com repetição – Equaciona Com Paulo Pereira
Acesso em: 28 de maio de 2022.
Permutação Simples e Permutação com Repetição – Brasil Escola
Acesso em: 28 de maio de 2022.
4ª Etapa: Cheque seus conhecimentos
Realizar questões de vestibular e do ENEM é um excelente exercício durante o estudo autodirigido. Isso porque essas questões são seguidas de gabarito, mesmo quando são dissertativas. Abaixo, alguns exemplos de questões sobre o tema estudado:
1. Considere uma fila de pessoas organizadas por ordem de chegada em que, em um determinado momento, há seis pessoas. De quantas formas diferentes essas pessoas poderiam estar ordenadas do primeiro ao último lugar?
Resolução:
Cada forma de ordenação é uma permutação simples, uma vez que os indivíduos são únicos e não se repetem. Dessa forma, havendo seis pessoas, a resposta é uma permutação com 6 elementos.
Dessa forma, calculamos:
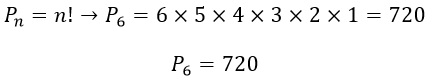
Seis pessoas podem estar ordenadas, em uma fila, de 720 maneiras distintas.
Disponível em: Toda Matéria.
Acesso em: 28 de maio de 2022.
2. Quantos números de algarismos distintos são possíveis formar com os algarismos ímpares, 3, 5, 7, 9?
a) 6
b) 16
c) 24
d) 120
e) 720
Resposta: D
Resolução:
Como há 5 algarismos, basta calcularmos a permutação de 5 elementos:
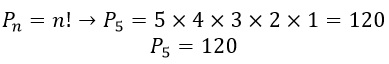
Disponível em: Brasil Escola.
Acesso em: 28 de maio de 2022.
3. O número de anagramas possíveis que podemos fazer com o nome BRASIL pode ser calculado por:
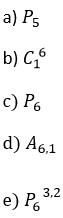
Resposta: C
Justificativa: Como o nome BRASIL possui 6 letras e nenhuma repetição, para calcular o total de anagramas basta calcularmos P6.
Numericamente, vale: P6 = 6! = 720
Disponível em: Brasil Escola.
Acesso em: 28 de maio de 2022.
4. Resolvendo a operação
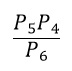
Encontraremos:
a) 2
b) 4
c) 6
d) 8
e) 10
Resposta: B
Resolução: 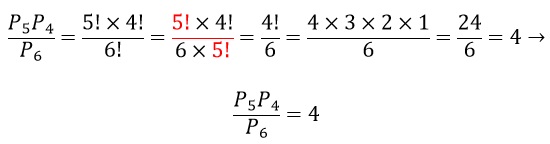
Disponível em: Brasil Escola.
Acesso em: 28 de maio de 2022.




