Conteúdos
Este plano de aula de física, astronomia e astronáutica apresenta um conteúdo que trata sobre velocidade de escape. Inicialmente, faz-se uma discussão introdutória, chamando a atenção para a característica atrativa do campo gravitacional, sendo ela a responsável por nos manter “presos” sobre a superfície do nosso planeta. Posteriormente, faz-se uma dedução simples da expressão matemática para a velocidade de escape. E, por último, são feitos os cálculos necessários para a obtenção dos valores das velocidades de escape de diversos astros do nosso Sistema Solar.
● Introdução;
● Velocidade de escape; e
● Cálculo da velocidade de escape de alguns astros do Sistema Solar.
Objetivos
● Compreender o que é velocidade de escape; e
● Aprender a calcular a velocidade de escape de diversos astros do Sistema Solar.
Ensine também:
Ônibus espacial: uma viagem para o espaço
Ondas gravitacionais e a teoria da relatividade
Palavras-chave:
Velocidade de escape. Aceleração gravitacional. Campo gravitacional. Força gravitacional. Sistema Solar. Planetas. Astros.
Previsão para aplicação:
4 aulas (50 min./aula).
1ª Etapa: Introdução
Uma característica de todos os corpos que possuem matéria diz respeito a sofrerem atração gravitacional, ou seja, corpos que possuem massa atraem-se¹ mutuamente. É por essa razão que estamos todos “presos” à superfície do planeta Terra. Isso pode até ser um fator tranquilizador para todos(as) os(as) atletas que realizam grandes saltos pois, por mais alto que saltem, sempre retornarão ao solo, jamais correndo o risco de acabarem indo para o espaço sideral.
Contudo, alguns objetos criados pela nossa espécie já saíram da Terra em direção ao nosso satélite natural, a Lua, bem como em direção a outros planetas do Sistema Solar. Alguns desses objetos já chegaram aos confins do nosso sistema estelar. Para objetos como foguetes, ônibus espaciais e naves conseguirem vencer a atração gravitacional do nosso planeta, é preciso algum tipo de força propulsora contínua, o que despende uma quantidade enorme de combustível.
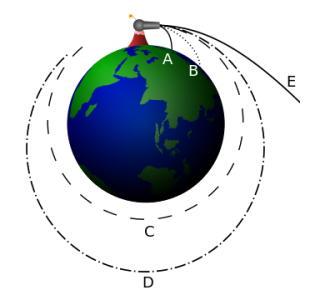
Quando não se está utilizando algum tipo de força propulsora contínua, como num foguete, por exemplo, existe alguma outra maneira de um objeto vencer a atração gravitacional que o mantém “preso” a um determinado astro (planeta, lua, asteroide, cometa)?
A resposta é sim. Pode-se arremessar um objeto com uma velocidade tal que, a partir de um valor mínimo, o objeto conseguirá vencer a atração gravitacional à qual estava submetido. Esse é o conceito de velocidade de escape.
Velocidade de escape é o valor mínimo que um objeto, submetido a um determinado campo gravitacional, precisa atingir para vencer a ação atrativa desse campo, “desprendendo-se” do mesmo, ou seja, o objeto não mais retornará.
¹ Diferentemente da força eletromagnética, que pode ser atrativa ou repulsiva, a gravidade (força gravitacional/campo gravitacional) possui um único comportamento: ela é apenas atrativa.
2ª Etapa: Velocidade de escape
Para obter a expressão matemática da velocidade de escape, deve-se considerar que a energia mecânica (E_(M )) do objeto lançado, no infinito, será nula. Lembrando que, nesse contexto, a energia mecânica é a soma da energia cinética (E_c) com a energia potencial gravitacional (E_g):


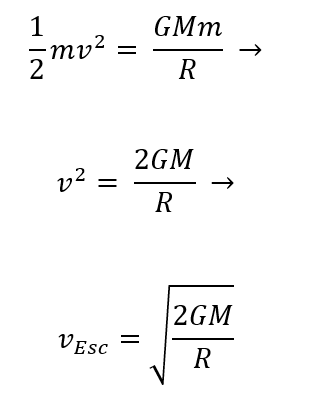
Desta forma, obtivemos a velocidade de escape mínima necessária para que um certo objeto, ao ser arremessado para fora de um campo gravitacional ao qual ele está submetido, possa escapar, sem retorno.
Na próxima etapa, iremos calcular o valor da velocidade de escape para diferentes astros do Sistema Solar.
3ª Etapa: Cálculo da velocidade de escape para alguns astros do Sistema Solar
Na etapa anterior, obtivemos a expressão matemática para calcular a velocidade de escape. Como podemos observar, a expressão da velocidade de escape não depende da massa do objeto que será arremessado para fora do campo gravitacional, mas apenas da massa do astro (M), do seu raio (R), e da constante da

A seguir, vejamos uma tabela com a massa e o raio de alguns astros do nosso Sistema Solar:
Tabela 1.: Massa e o raio médio de alguns astros do Sistema Solar
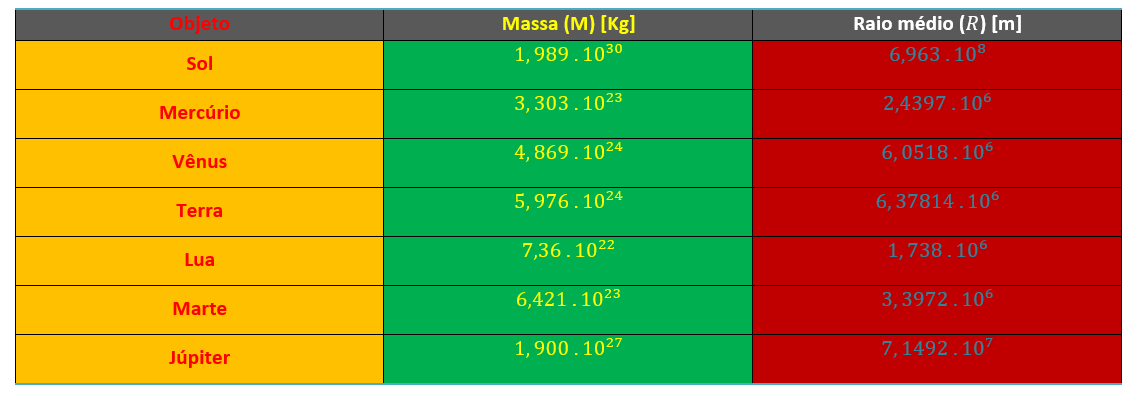
De posse desses dados, calculamos agora a velocidade de escape para cada um desses astros:
1) Velocidade de escape para o Sol

2) Velocidade de escape para Mercúrio
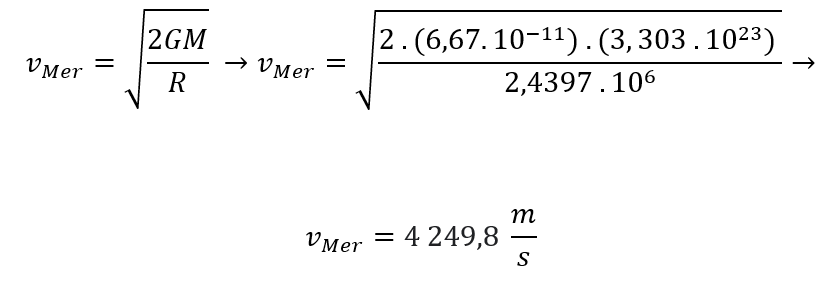
A velocidade de escape do planeta Mercúrio é de 4 249,8 m/s, ou de aproximadamente 4,3 Km/s.
3) Velocidade de escape para Vênus

4) Velocidade de escape para a Terra

5) Velocidade de escape para a Lua

6) Velocidade de Escape para Marte

7) Velocidade de Escape para Júpiter
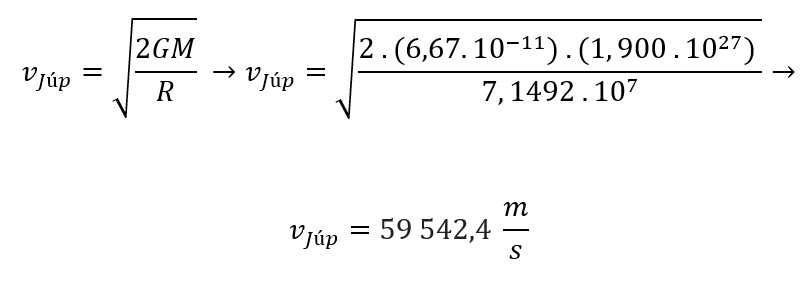
A velocidade de escape do planeta Júpiter é de 59 542,4 m/s, ou de aproximadamente 59,5 Km/s.
Como todas as grandezas estão representadas de acordo com o SI, as velocidades de escape para cada astro têm como unidade de medida o metro por segundo [m/s].
Naturalmente, os mesmos cálculos podem ser reproduzidos para os demais corpos do Sistema Solar, tais como: os planetas Saturno, Urano e Netuno, os planetas anões (Plutão e outros), as luas, os cometas, os asteroides e quaisquer corpos que possuam um campo gravitacional considerável, estando ele dentro do Sistema Solar ou não.
Tal tarefa pode ser indicada como exercício e/ou trabalho escolar para os/as estudantes.
A seguir, temos uma nova tabela com os valores calculados das velocidades de escape de cada um dos astros do Sistema Solar da Tabela 1, nas unidades de medida metros por segundo [m/s] e quilômetros por segundo [Km/s]:
Tabela 2: Velocidade de escape dos astros
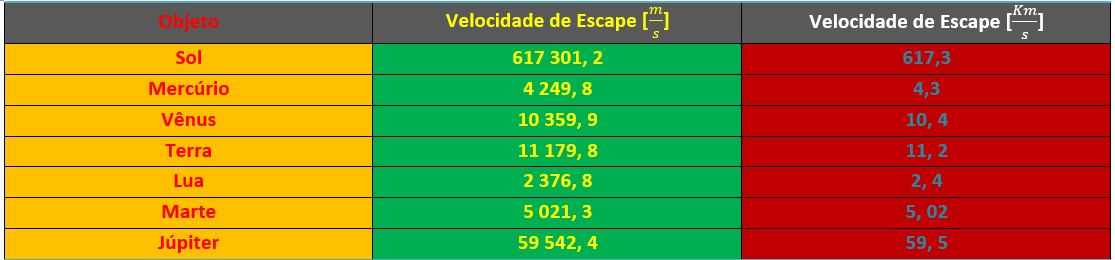
Este material pode ser utilizado também como um ponto de partida para a introdução do conceito de buraco negro, pois a principal característica desse objeto astrofísico exótico é o fato dele possuir uma velocidade de escape maior do que a velocidade da luz (c=299 792 458 m/s), ou seja, nada consegue escapar da atração de seu campo gravitacional, nem mesmo a luz, razão pela qual tal objeto foi assim batizado.
Plano de aula elaborado pelo Professor Elves Silva Moreira.
Coordenação pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.
Materiais Relacionados
● Para ver conteúdos sobre velocidade de escape:
UFRGS
Acesso em: 26 de setembro de 2021.
Brasil Escola
Acesso em: 26 de setembro de 2021.
Mundo Educação
Acesso em: 26 de setembro de 2021.
● Para ver vídeos sobre velocidade de escape:
Velocidade de Escape em 3 min! – Professor Octavio
Acesso em: 26 de setembro de 2021.
Física – Velocidade de Escape – ExplicaMais
Acesso em: 26 de setembro de 2021.

