Conteúdos
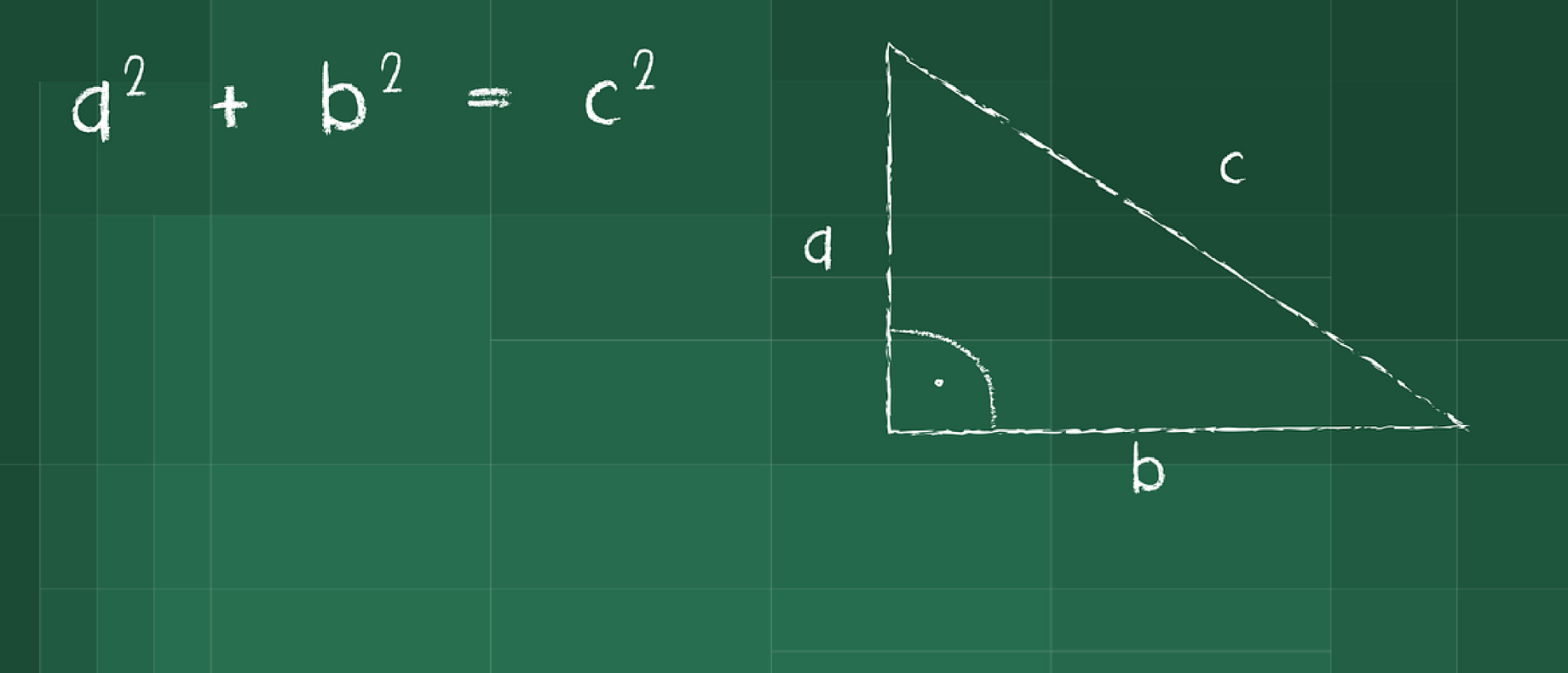
– Teorema de Pitágoras
– Potenciação
– Equação do 2º grau
– Conversão de unidades
– Velocidade média
Objetivos
– Realizar uma estimativa da trajetória de uma bola durante um chute no travessão
– Aplicar o Teorema de Pitágoras em uma situação esportiva
– Fazer cálculos aproximados de distância e velocidade média
1ª Etapa: Início de conversa
Quando se trata de aplicações do Teorema de Pitágoras, é muito comum encontrar exercícios sobre a sombra de prédios, escadas encostadas em uma parede ou altura de uma árvore ou poste. Porém, aplicando as devidas aproximações, é possível inserir esse conceito em temas mais próximos da realidade dos alunos.
Aplicar conceitos matemáticos em situações esportivas pode ser uma ótima oportunidade de conseguir atenção e maior participação dos alunos em sala de aula. O (A) professor (a) poderá iniciar a conversa perguntando aos alunos como pode ser feito o cálculo da trajetória de uma bola durante uma tentativa de chute ao gol.
Nessa etapa, pode ser mais eficiente o (a) professor (a) utilizar recursos visuais, como vídeos de lances famosos em campeonatos de futebol, análises de programas esportivos etc., assim, os alunos poderão visualizar a situação investigativa (chutes no travessão). Sugerimos a exibição do vídeo abaixo indicado, onde Neymar passa pelo desafio de chutar bolas no travessão.
– Assista ao vídeo “Neymar é desafiado a chutar cinco bolas no travessão. Veja como se saiu o craque!”.
2ª Etapa: Cálculo da trajetória
É possível estimar a trajetória da bola durante um chute no travessão, pois:
a) a trajetória tem início na posição do jogador que chuta;
b) a trajetória termina na trave do gol e, portanto, tem-se o valor da altura no instante final;
c) os dados de comprimentos são facilmente aproximados, a partir das medidas do campo de futebol;
d) a trajetória pode ser aproximada por uma reta.
Observe o esquema abaixo:
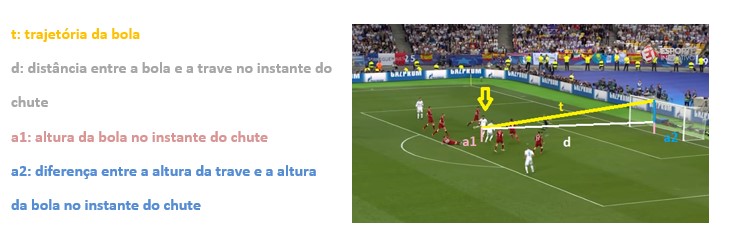 Aproximando o esquema para um triângulo retângulo, temos:
Aproximando o esquema para um triângulo retângulo, temos:
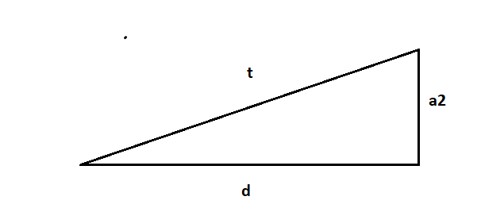
Para calcular o valor de t, é necessário fazer aproximações para os valores d e a2. Nessa etapa, é interessante que as aproximações sejam feitas pelos alunos com a ajuda do (a) professor (a) pois, dessa forma, os estudantes estarão envolvidos em todas as etapas da resolução, discutindo critérios para decidir quais são os melhores valores para serem utilizados a partir de argumentações matemáticas de proporção, medidas etc.
Utilizando as medidas oficiais como referência, considere d = 12 m e a2 = 2 m e t a hipotenusa do triângulo retângulo acima. Dessa forma, basta aplicar o Teorema de Pitágoras para encontrar o valor de t:
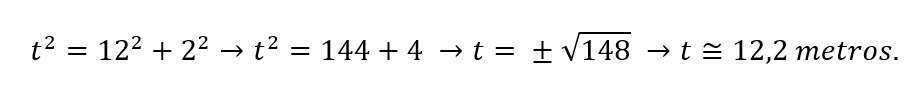 Podemos concluir que, utilizando os valores aproximados acima, a trajetória da bola, nesse lance, foi de aproximadamente 12,2 metros.
Podemos concluir que, utilizando os valores aproximados acima, a trajetória da bola, nesse lance, foi de aproximadamente 12,2 metros.
3ª Etapa: Cálculo da velocidade média
Caso julgue interessante, o (a) professor (a) poderá fazer uma estimativa da velocidade média da bola. Sabe-se que a velocidade média é dada pela razão entre a distância e o tempo e, aproximando o tempo da trajetória para pouco mais que meio segundo, podemos encontrar a velocidade média:
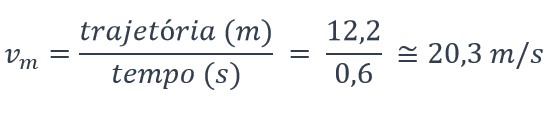
Materiais Relacionados
1 – Para ver uma demonstração do Teorema de Pitágoras utilizando a fórmula de Bhaskara, assista ao vídeo “Demonstração do Teorema de Pitágoras por Bhaskara”.
2 – Exemplos de aplicações do Teorema de Pitágoras podem ser vistos no artigo: “A matemática em nosso dia a dia: mais constante do que imaginamos”.
3 – Para encontrar medidas oficiais e curiosidades sobre o futebol: “Tudo sobre as medidas do futebol”. E também em “Medidas do campo de futebol”.