Conteúdos
– Leis de Newton
– Momento de uma força ou torque
Objetivos
– Estudar o conceito de momento de uma força
– Compreender as condições para o equilíbrio rotacional de um corpo extenso
1ª Etapa: Início de conversa
O tema da aula envolve o conceito de momento e equilíbrio. Antes de iniciar com formulações teóricas, é importante que o(a) professor(a) apresente exemplos do cotidiano que envolvam o conceito de momento e equilíbrio, assim como estimular a participação dos alunos para que deem outros exemplos.
Para essa aula, os alunos utilizarão o Objeto Virtual de Aprendizagem (OVA) Balançando, elaborado pela PhET Interactive Simulations. Este OVA possui três opções de manuseio: Introdução, Laboratório de Equilíbrio e Jogo (FIGURA 1).

Figura 1. Tela inicial do OVA Balançando.
2ª Etapa: Introdução
Na primeira opção de manuseio, será possível entender o funcionamento do OVA. Sugere-se que se inicie pela investigação do movimento de uma gangorra: a) em equilíbrio (FIGURA 2A), em torno de seu eixo de rotação; b) quando alguma massa é colocada sobre o lado direito do ponto de referência, a gangorra pode girar no sentido horário (FIGURA 2B); c) caso a massa seja colocada no lado esquerdo, o sentido da rotação será anti-horário (FIGURA 2C). Se faz necessário que o(a) professor(a) delimite o conceito de equilíbrio, pois, nessa aula, trabalharemos com o equilíbrio rotacional.
A
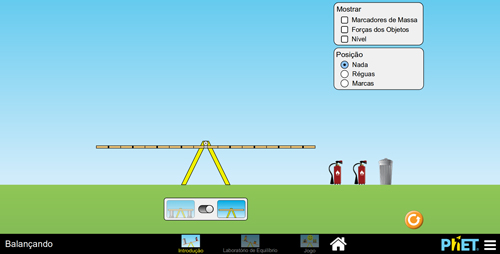
B
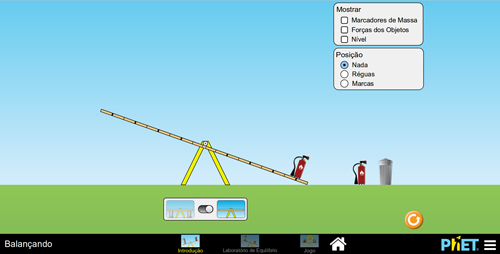
C
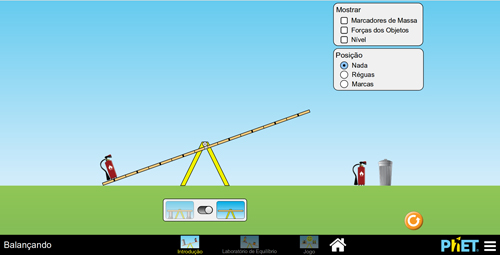
Figura 2. Gangorra: A – em equilíbrio; B – com movimento horário; C – com movimento anti-horário.
Em seguida, o(a) professor(a) poderá propor o Desafio do Equilíbrio. Nessa atividade, os estudantes serão desafiados a equilibrar a gangorra em dois casos: 1) usando objetos de mesma massa; 2) usando dois objetos de massa diferente; 3) usando três objetos.
Por tentativas e erros, os alunos chegarão nos casos ilustrados na Figura 3. Para equilibrar dois objetos de mesma massa, é preciso que eles sejam colocados na mesma distância do eixo de rotação da gangorra (FIGURA 3A). Já no caso das Figuras 3B e 3C, o equilíbrio é obtido posicionando adequadamente objetos de massas diferentes, em diferentes distâncias do eixo rotacional.
A
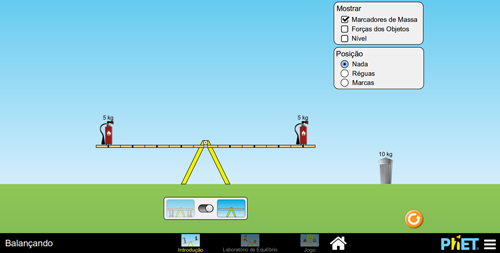
B
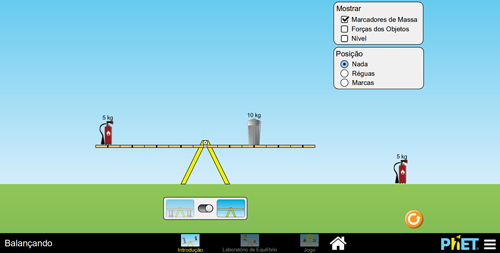
C
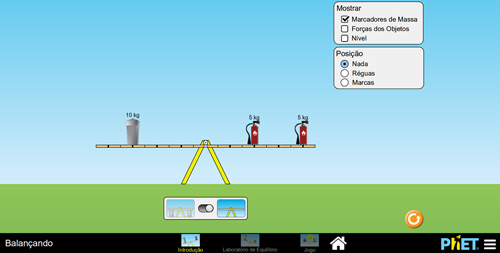
Figura 3. Exemplificação do Desafio do Equilíbrio: A – com dois objetos de massas iguais; B – com dois objetos de massas diferentes; C – com três objetos.
3ª Etapa: Calculando momento
Na primeira aula, os alunos usaram o OVA para trabalhar com o conceito de equilíbrio de forma intuitiva. Os estudantes foram capazes de inferir que, quando a gangorra permanece em equilíbrio, ela não gira nem no sentido horário, nem no anti-horário. Além disso, constataram que para equilibrar os objetos era preciso manipular duas variáveis: massa e distância.
Nessa segunda aula, a turma passará a receber orientação do(a) professor(a), explorando a formulação teórica e racionalização matemática dos fenômenos de momento e equilíbrio. Para isso, o(a) professor(a) poderá usar a opção de manuseio Laboratório de Equilíbrio (Figura 4).
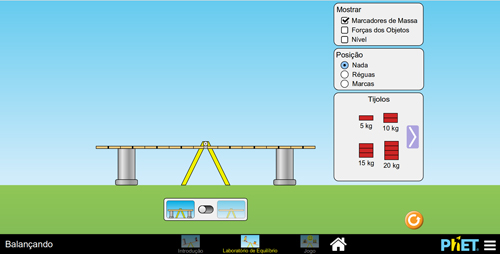
Figura 4. Tela inicial da modalidade Laboratório de Equilíbrio.
A grandeza física associada ao movimento de rotação de um determinado corpo em razão da ação de uma força é denominada torque (ou momento), o qual é definido como o produto da força F aplicada pela distância que separa o ponto de aplicação dessa força ao eixo (1).
|M| = F · d (1)
Para explicar como que se calcula o momento, o(a) professor(a) precisará selecionar no OVA a opção “régua”. Com essa ferramenta é possível medir a distância do eixo ao local de aplicação da força.
Outro ponto importante é apontar o motivo pelo qual o cálculo do momento é realizado em módulo e porque o sinal é determinado posteriormente ao cálculo. Para isso, o(a) professor(a) poderá adotar uma convenção como a que é explicada aos 9 min e 10s do vídeo: “Torque ou Momento”. Em suma, é adotada a seguinte notação: se a rotação for no sentido horário, o momento ou torque será negativo mas, se a rotação for no sentido anti-horário, o momento ou torque será positivo.
A partir da situação ilustrada na Figura 5, pode-se exemplificar o procedimento do cálculo de momento.
A
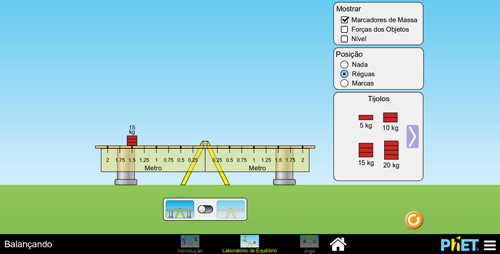
B
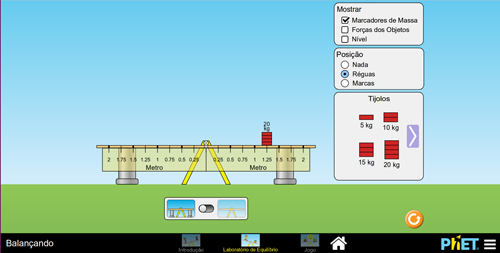
Figura 5. Situação para exemplificar o cálculo de momento. A – a rotação será no sentido anti-horário; B – a rotação será no sentido horário.
CASO A1: m = 15kg; d = 1,5m; rotação no sentido anti-horário
|M| = F · d
|M| = m · g · d
|M| = 15 · 10 · 1,5 = 225 N.m
M = + 225 N.m (positivo porque a rotação será no sentido anti-horário)
CASO B: m = 20kg; d = 1,25m; rotação no sentido horário
|M| = F · d
|M| = m · g · d
|M| = 20 · 10 · 1,25 = 250 N.m
M = – 250 N.m (negativo porque a rotação será no sentido horário)
1 Observação: no exercício, a força aplicada é a força peso, portanto: F = m · g; onde g é a aceleração da gravidade.
Com a situação ilustrada na Figura 6, pode-se exemplificar o procedimento do cálculo de momento quando colocado mais de um objeto. Para isso, basta somar os momentos que cada força aplica, conforme expresso em (2).
Mtotal = F1d1 + F2d2 + . . . + Fndn (2)
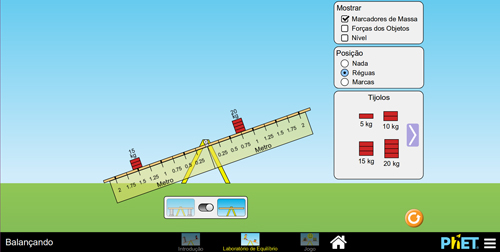
Figura 6. Dois objetos na gangorra.
Observe que, na Figura 6, foram colocados dois objetos na gangorra. No lado esquerdo, um objeto de 15kg a 1,5m de distância do eixo de rotação e, no lado direito, um objeto de 20kg a 0,75m de distância do eixo de rotação. A primeira etapa é calcular os momentos individuais e depois somá-los.
– Objeto do lado esquerdo
|M| = F1 · d1
|M| = m · g · d
|M| = 15 · 10 · 1,5 = 225 N.m
M1 = + 225 N.m (positivo porque, caso estivesse sozinho, a rotação seria no sentido anti-horário)
– Objeto do lado direto
|M| = F2 · d22
|M| = m · g · d
|M| = 20 · 10 · 0,75 = 150 N.m
M2 = – 150 N.m (negativo porque, caso estivesse sozinho, a rotação seria no sentido horário)
– Cálculo do momento total
Mtotal = F1d1 + F2d2
Mtotal = +225 + (-150) = +225 – 150 = + 75
Como o resultado do momento total é positivo, todo o sistema está rotacionando no sentido anti-horário, o que corrobora a convenção que é adotada.
4ª Etapa: Equilíbrio rotacional
Veja um caso especial, o equilíbrio rotacional, isto é, quando a gangorra não rotaciona no sentido horário, nem no sentido anti-horário (Figura 7).
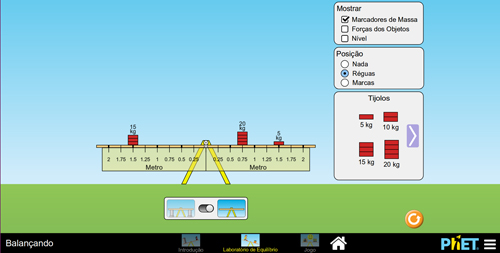
Figura 7. Um caso de equilíbrio rotacional.
• Objeto 1 → m = 15kg; d = 1,5m; rotação: sentido anti-horário (caso estivesse sozinho)
|M| = F1 · d1
|M| = m · g · d
|M| = 15 · 10 · 1,5 = 225 N.m
M1 = + 225 N.m
• Objeto 2 → m = 20kg; d = 0,75m; rotação: sentido horário (caso estivesse sozinho)
|M| = F2 · d2
|M| = m · g · d
|M| = 20 · 10 · 0,75 = 150 N.m
M2 = – 150 N.m
• Objeto 3 → m = 5kg; d = 1,5m; rotação: sentido anti-horário (caso estivesse sozinho)
|M| = F3 · d3
|M| = m · g · d
|M| = 5 · 10 · 1,5 = 75 N.m
M3 = – 75 N.m
– Cálculo do momento total
Mtotal = F1d1 + F2d2 + F3d3
Mtotal = +225 + (-150) + (-75) = +225 – 150 – 75 = + 75
Mtotal = +225 – 150 – 75
Mtotal = 0
A partir do exemplo da Figura 7, os estudantes ampliam seus conhecimentos, pois foi acrescido à percepção sensorial a racionalização física e matemática de que um sistema está em equilíbrio rotacional quando o momento total do for igual a zero.
5ª Etapa: O jogo
Para finalizar a aula, o(a) professor(a) poderá usar a opção de manuseio Jogo (FIGURA 8), para que os alunos pratiquem aquilo que aprenderam.
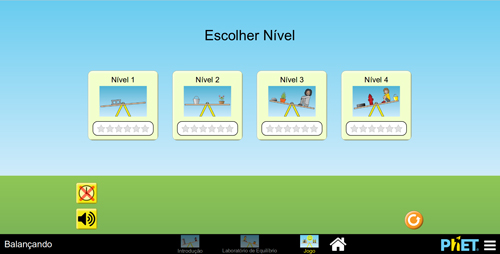
Figura 8. Tela inicial da modalidade Jogo.
É possível jogar em 4 níveis de dificuldade, porém, as regras são basicamente duas: deverão colocar um objeto para equilibrar o sistema (FIGURA 9A) ou conferir se o sistema dado estará em equilíbrio ou se será rotacionado no sentido horário ou no sentido anti-horário (FIGURA 9B).
A
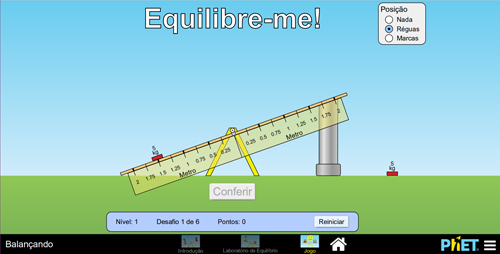
B
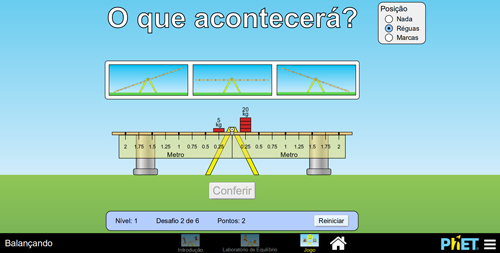
Figura 9. Regras do jogo: A – Executar o equilíbrio; B – Responder o que acontece no sistema.
O(a) professor(a) deverá mediar a atividade de modo que os estudantes a executem por meio da formulação matemática e/ou do raciocínio lógico, ao invés da tentativa e erro. Um meio de fazer essa mediação seria realizando alguns jogos com a turma. Na Figura 10 é apresentado um exemplo do jogo e, logo em seguida, a resolução.
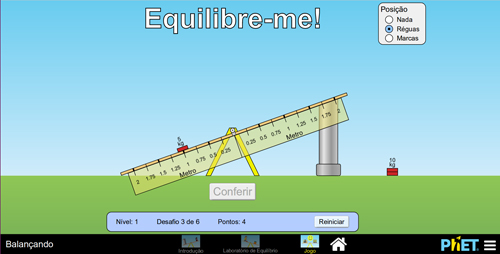
Figura 10. Tela inicial da modalidade Jogo.
Para resolver esse problema, deve-se levar em consideração que, para formar o equilíbrio, o segundo objeto precisa ser colocado no lado oposto do primeiro objeto. Além disso, a soma dos momentos deve ser igual a zero. Logo:
Mtotal = F1d1 + F2d2
0 = 5 · 10 · 1 – 10 · 10 · d
0 = 50 – 100d
d = -50/-100
d = 0,5 m
Como são muitos jogos, cada aluno deverá continuar em casa.
6ª Etapa: Finalizando a discussão
Na sexta e última aula, o(a) professor(a) poderá questionar as dificuldades que a turma teve com o jogo. Além disso, poderá ser resolvido alguns exercícios de vestibular sobre o tema momento. Seguem algumas sugestões com os respectivos gabaritos:
1. (IF-GO) O móbile é um modelo abstrato que tem peças móveis, impulsionadas por motores ou pela força natural das correntes de ar. Suas partes giratórias criam uma experiência visual de dimensões e formas em constante equilíbrio. O móbile foi inicialmente sugerido por Marcel Duchamp para uma exibição de 1932, em Paris, sobre certas obras de Alexander Calder, que se converteu no maior exponente da escultura móbile. A origem latina do termo móbile remete à ideia de “móbil”, “movimento”. A figura a seguir representa um tipo de móbile.
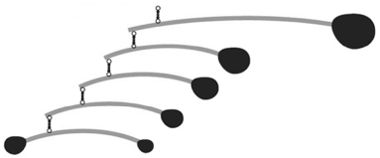
Para que o equilíbrio do móbile ocorra, é necessário e suficiente que
a) as massas penduradas nas extremidades de cada haste sejam iguais.
b) a força resultante e o torque sobre cada uma das hastes sejam nulos.
c) a força resultante sobre cada haste seja nula.
d) o torque jamais seja nulo.
e) haja conservação da energia mecânica.
Resposta correta: B
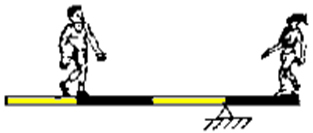
2. (UFV) Um rapaz de 900 N e uma garota de 450 N estão em uma gangorra. Das ilustrações abaixo, a que representa uma situação de equilíbrio é:
a)
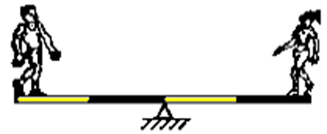
b)
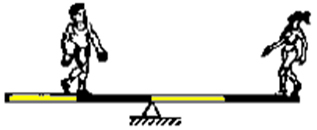
c)
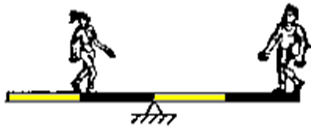
d)
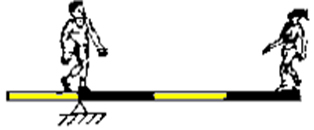
e)
Resposta correta: B
3. (UFPE-PE) A figura representa a força aplicada na vertical, sobre uma chave de boca, por um motorista de caminhão tentando desatarraxar uma das porcas que fixa uma roda. O ponto de aplicação da força dista 15 cm do centro da porca e o módulo da força máxima aplicada é F = 400 N. Nesta situação, suponha que o motorista está próximo de conseguir desatarraxar a porca.
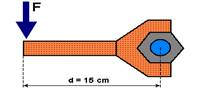
Em seguida, o motorista acopla uma extensão à chave de boca, de forma que o novo ponto de aplicação da força dista 75 cm do centro da porca. Calcule o novo valor do módulo da força, F’, em newtons, necessário para que o motorista novamente esteja próximo de desatarraxar a porca.
Resposta correta:
Para conseguir desatarraxar a porca, só com a chave de 15 cm (0,15m):
|M| = F1 · d1
M1 = 400 · 0,15
M1 = 60 N.m
Então, quando colocarmos uma chave maior, de 75 cm (0,75 m), o momento angular tem que ser o mesmo para que consigamos girar a porca igualmente:
|M| = F2 · d2
M2 = F2 · 0,75
como M2 = M1
F2 · 0,75 = 60
F2 = 60/0,75
F2 = 80N
Materiais Relacionados
Recomenda-se que o(a) professor(a) acesse algum material preliminar para conhecer um pouco mais sobre momento e equilíbrio:
1 – “Divulgação científica no ensino de Física: Torque e Momento angular”. Acesso em: 18 de setembro de 2018.
2 – “Construção do conceito de ‘momento de uma força a partir de experimentos relacionados ao cotidiano”. Acesso em: 18 de setembro de 2018.
3 – “Alguns aspectos da Física Mecânica e Dança: procedimentos técnico-criativos”. Acesso em: 18 de setembro de 2018.

