Conteúdos
– Limites
Objetivos
– Compreender a ideia intuitiva de limite;
– Aplicar a ideia intuitiva de limites para resolver problemas simples.
1ª Etapa: Início de conversa
O estudo de limites como conhecemos é algo novo. A definitiva formalização desta teoria para linguagem moderna deu-se há aproximadamente 150 anos, no entanto, a curiosidade da humanidade pela ideia de limite é muito anterior. Imaginar o que acontece ao aproximar-se tanto quanto é possível de um determinado ponto ou situação é um exercício de profunda reflexão.
Apesar deste tópico apresentar-se de forma tão interessante em diversos contextos, dentro e fora da matemática, não há muito espaço para sua abordagem no ensino médio. Este plano de aula objetiva introduzir o conceito de limite matemático por meio de três situações: aproximação de um ponto por meio de intervalos, aproximação da circunferência por meio de polígonos regulares e a aproximação de 1 por meio de reais (1=0,999…).
2ª Etapa: Motivação dos estudantes
Inicie à aula apresentando uma sequência de fotos que mostre uma raquete de tênis golpeando uma bola.




O(a) professor(a) pode motivar o grupo utilizando estas imagens. Se possível, use um projetor para exibi-las em sala de aula. Caso não tenha esta possibilidade, um simples desenho na lousa representando esta situação é suficiente.
Introduza o conceito de limite direcionando o grupo a refletir sobre como poderia estimar qual seria a posição da bolinha de tênis nos milésimos de segundo que faltam. Veja um exemplo de como realizar esta abordagem:
Suponhamos que, por um defeito, a câmera que gravou o vídeo acima, não registrou o momento 0:00.1. Qual seria a posição da bolinha de tênis em 0:00.1?
Como sabemos que a bolinha não pode se “teletransportar”, temos a intuição de que esta deveria estar em algum ponto entre as posições fotografadas no momento 0:00 e 0:00.2.
Imagine que dispomos de uma filmadora com grande capacidade de quadros por segundo para registrar este momento, poderíamos afirmar que, para localizar a posição aproximada da bolinha em 0:00.1 bastaria congelar o vídeo em algum momento entre 0:00.099 e 0:00.101. É importante que o(a) professor(a) destaque neste momento que, de fato, não poderemos observar a imagem da bolinha em 0:00.1. Lembre-se de que estamos procurando uma boa aproximação para a imagem.
Vamos um pouco mais longe. Pense que nossa filmadora possui tantos quadros por segundo quanto podemos imaginar. Qual seria a melhor aproximação de 0:00.1 (sabendo que o quadro 0:00.1 foi deletado!)? Esta pergunta não tem uma resposta precisa, pois podemos nos aproximar por meio de um intervalo tão pequeno quanto é possível imaginar, no entanto, sem nunca alcançar o ponto que falta.
É o conceito de limite que lida com este tipo de problema. Quando estamos falando de limites, estamos interessados em nos aproximar tão perto quanto é possível de uma determinada situação.
Espera-se que o grupo se aprofunde nesta discussão com a mediação do professor. Explore este momento ilustrando o problema na lousa. Você pode traçar uma reta que representa a linha de gravação e mostrar aos estudantes que é sempre possível se aproximar ainda mais do ponto 0:00.1.

3ª Etapa: A intuição de limites na geometria
Depois desta exposição, motive a discussão debatendo quais outros significados à expressão “tão perto quanto é possível” pode ter. Em seguida, direcione o debate para o problema de se aproximar tão perto quanto é possível de uma circunferência por meio de polígonos regulares.
Comece com a tentativa a partir de um triângulo regular e mostre que com um número suficientemente grande de lados é possível obter uma aproximação satisfatória de uma circunferência.
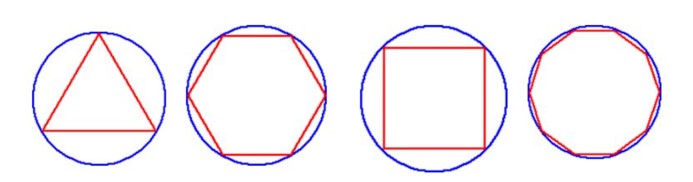
Aqui uma aproximação satisfatória significa que a diferença entre o polígono obtido e a circunferência será tão pequena quanto podemos imaginar. Isto é, a diferença entre as figuras é desprezível!
4ª Etapa: 0,999... = 1?
Utilizando estes conceitos, responderemos à curiosa pergunta que intitula este plano de aulas. Na lousa, escreva a seguinte pergunta:
0,999… = 1?
Estimule os alunos a partilharem suas respostas e a utilizarem as discussões anteriores envolvendo limites em seus argumentos. Após este momento, provoque o grupo com outras perguntas como:
– Se estes valores são iguais, como podem ter representações tão diferentes?
– Se estes valores são diferentes, qual é a diferença entre eles?
Este tipo de pergunta estimulará reações tanto dos alunos que acham que esses valores são iguais quanto daqueles que acreditam que esses valores são distintos.
Para a primeira das perguntas, vale relembrar que há várias maneiras de se representar as mesmas quantidades. Um bom exemplo é a representação decimal de uma fração ou frações equivalentes.
A segunda pergunta tem de ser tratada utilizando conceitos abordados nas reflexões das etapas anteriores. Destaque que a diferença entre 0,999… e 1 deve ser um número tão pequeno quanto é possível imaginar. Portanto, 0,999… é tão próximo quanto é possível chegar de 1. Ora! Qual é o número tão próximo quanto é possível chegar de 1? É claro que é o próprio número 1!
Esta argumentação pode ser demasiadamente abstrata para alguns jovens. Por este motivo, é importante apresentar também uma prova algébrica deste fato. Veja a seguir uma sugestão desta prova:
x=0,999…
10x=9,999…
10x-x=9,999… – 0,999…
9x=9
x=1
Portanto, 0,999…=1.
Encerre retomando a trajetória deste plano de aula e abrindo, se possível, espaço para dúvidas ou comentários sobre o tema trabalhado em sala de aula. Incentive às reflexões e direcione às discussões.