Conteúdos
– Exponenciação
– Número neperiano
– Umidade relativa e específica
– Experimento
Objetivos
– Reconhecer a exponenciação em atividades cotidianas
– Entender como surgiu o número neperiano
– Aprender o conceito de pressão de vapor de saturação aplicado à equação de Clausis e Clapeyron
– Compreender a diferença entre umidade relativa e específica
– Discussão física de variáveis meteorológicas
– Produção de gráficos
Previsão para aplicação:
2 aulas conceituais (50 min./aula) + 1 aula experimental (50 min)
1ª Etapa: Início de conversa
Para iniciar, ou mesmo revisar, o conceito das exponenciais, o(a) professor(a) pode utilizar o segundo capítulo do livro “Bilhões e bilhões” de Carl Sagan: “O tabuleiro de xadrez persa”. Neste capítulo, o autor descreve uma anedota da recompensa pedida por um grão-vizir a um rei pela invenção do jogo do xadrez. Apesar de parecer uma recompensa ingênua à primeira vista, o número em questão atinge valores altíssimos, da ordem de quintilhões depois de um certo tempo. No decorrer do capítulo, outros exemplos são citados pelo autor. Dependendo da oferta de exemplares do livro na biblioteca, os(as) estudantes podem ser convidados(as) a ler o capítulo e trazer um exemplo de exponencial que aparece no cotidiano e que não é citado no livro. A seguir, o número neperiano (ou número de Euler) deve ser abordado. Existem muitas situações em que o número neperiano aparece (ver o link na seção “Materiais Relacionados”), de forma que este tópico oferece uma boa oportunidade de se trabalhar interdisciplinarmente com outros(as) docentes. O exemplo mostrado no mesmo link entre 0:47 a 1:53 pode ser reproduzido em sala de aula, utilizando uma calculadora. O(A) professor(a) deve incentivar a participação dos(as) estudantes para os cálculos de porcentagem.
2ª Etapa: Entendo pressão de vapor
A atmosfera é constituída majoritariamente por nitrogênio e oxigênio. Entretanto, há uma vasta presença de outros gases, em especial, o vapor d’água. Esses gases contribuem para a pressão atmosférica, de forma que, quanto maior a concentração de um gás, maior a sua participação na pressão. Neste momento, o conceito da Lei de Dalton das pressões parciais pode ser explorado (utilizar material disponível na seção “Materiais Relacionados” para revisar ou introduzir o conceito). A pressão exercida pelo vapor d’água recebe o nome de pressão de vapor d’água (e). Existe uma quantidade máxima que a atmosfera comporta de vapor d’água, a chamada pressão de vapor de saturação (es), que depende exclusivamente da temperatura do ar (T). É importante diferenciar a notação entre o número de Euler e a pressão de vapor (ambas representadas pela letra e). Quanto maior a temperatura, mais vapor d’água cabe na atmosfera. O cálculo de es pode ser descrito pela equação de Clausius e Clapeyron (veja link na seção “Materiais Relacionados” para aprofundamento), que depende do calor latente de vaporização, da constante dos gases para o vapor d’água, além da temperatura do ar, no expoente do número neperiano.
3ª Etapa: Exercício #1
A equação de Clausius e Clapeyron para a pressão de vapor de saturação aparece de formas diversas na literatura porque depende do intervalo de temperatura em que se é aplicada. Utilizando o link disponível na seção inicial, compare as equações de Buck, Tetens e Bolton. Quais as semelhanças e diferenças entre elas? O que o coeficiente que multiplica a exponencial significa? Os(As) estudantes são convidados(as) a pesquisar sobre o ponto triplo da água, e espera-se que o valor do coeficiente seja identificado como a pressão em que a água ocorre em suas três fases: vapor, líquido e sólido.
Na sequência, utilizando uma planilha de Excel e projetando para a sala, as equações devem ser comparadas para um mesmo intervalo de temperaturas. Neste momento, uma discussão sobre as unidades envolvidas e a magnitude da pressão atmosférica podem ser provocadas.
4ª Etapa: Umidades relativa e específica
A umidade relativa do ar é a razão entre a quantidade de vapor disponível na atmosfera pela quantidade máxima possível. Essas quantidades podem ser representadas, por exemplo, pela pressão parcial de vapor d’água na atmosfera e pela pressão de vapor de saturação, respectivamente. O(A) docente pode perguntar à sala: “Quantas pessoas cabem assentadas nessa sala?”, “E quantas pessoas estão ocupando esses espaços?”. Escrevendo na lousa, o(a) docente calcula a razão entre os(as) ocupantes pela quantidade máxima possível. “Analogamente, é isso que a umidade relativa mostra: o quanto de umidade um dado volume tem (e) pelo máximo que ele pode ter (es), ou seja, UR=e/es“.
Com a pergunta “Costuma ser mais úmido durante o dia ou durante a noite?”, deve-se discutir o efeito da temperatura na umidade relativa. Como à noite a temperatura costuma ser mais baixa, precisa-se de menos vapor d’água para saturar a atmosfera, ou seja, es é mais baixa à noite do que durante o dia (se o exercício da seção anterior foi aplicado em sua totalidade, salientar a curva es(T)).
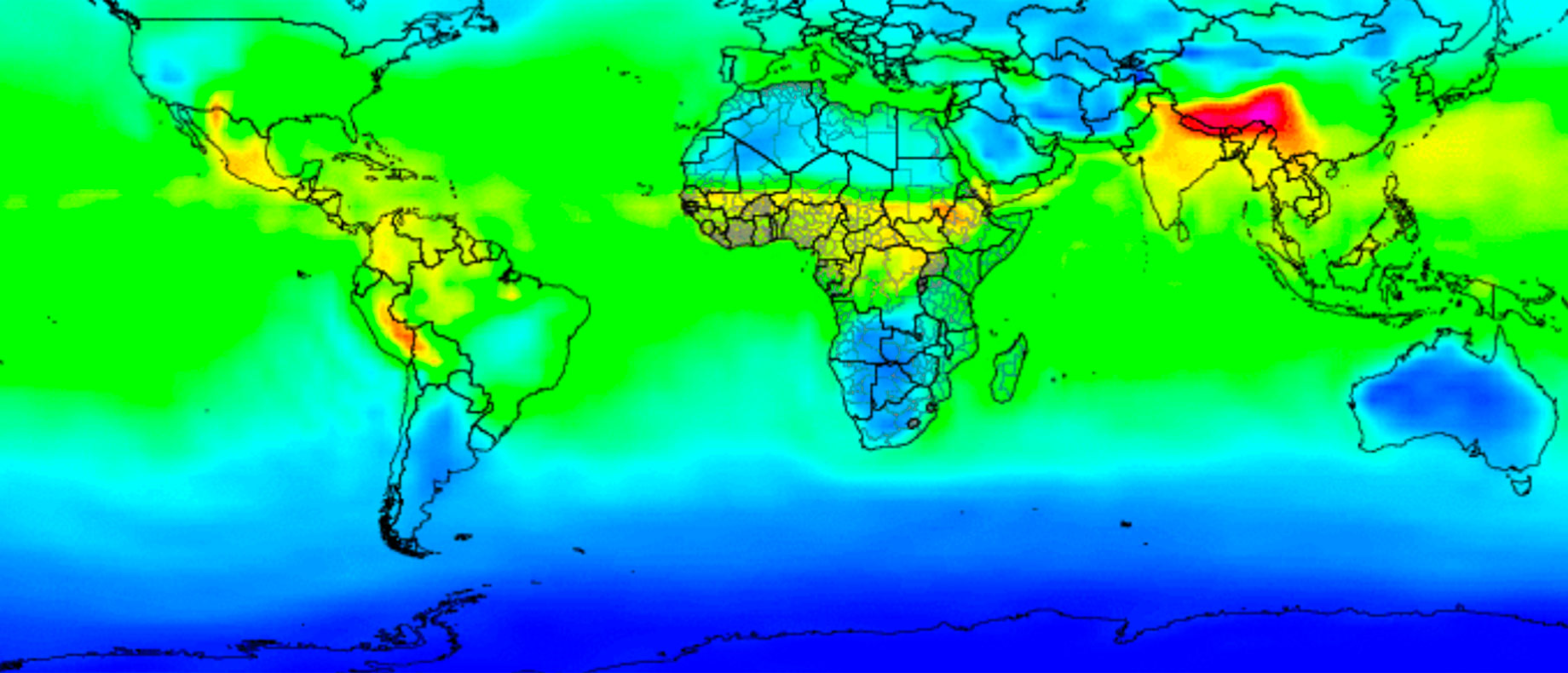
Projetando a imagem disponível na seção de links, e questionando: “Ter umidade relativa alta significa ter muito vapor d’água na atmosfera?”, o(a) docente deve coletar as respostas dos(as) estudantes. Em contraponto, ajustando o mapa de umidade específica (também disponível na seção de links) para um mês de verão (por exemplo, 21-31 Jan 2019) e outro de inverno (21-31 Jul 2019), é possível notar que a umidade específica tem um padrão distinto da umidade relativa. Isso se deve pela umidade específica representar algo diferente: é a razão entre a massa de ar úmido em um dado volume de ar pela massa total desse volume (ar seco + ar úmido), geralmente expressa em g/kg. Ou seja, a umidade específica não depende da temperatura, mas apenas da quantidade de vapor d’água na atmosfera.
5ª Etapa: Experimento com higrômetro
Este exercício necessita de um (ou mais) termo-higrômetro(s), instrumento que mede a temperatura e a umidade do ar, e existem opções para compra com preços acessíveis. A ideia é utilizar esses equipamentos para monitorar essas variáveis em um local ou em diferentes lugares da cidade/bairro.
Uma primeira abordagem seria anotar os valores medidos pelo termo-higrômetro tanto de temperatura quanto de umidade por um intervalo de tempo, por exemplo, a cada 10 minutos por 2 a 3 horas. Com a possibilidade de se ter mais de um instrumento, a sala pode ser dividida em grupos que medirão a temperatura e a umidade em diferentes pontos da cidade/bairro, em locais que contrastem entre si, por exemplo, em um parque arborizado e no centro da cidade, nas margens de um lago, dentro de uma residência, entre outros lugares. As medidas devem ser tomadas em um mesmo intervalo para os pontos diferentes, e a ocorrência de chuva, fortes ventos, sombreamento por nuvens, entre outras coisas, devem ser anotadas. É preciso organizar um protocolo inicialmente para mostrar o funcionamento do instrumento e como se darão as medidas (passo de tempo, intervalo, revezamento de funções entre estudantes).
Com as medidas efetuadas, os resultados devem ser apresentados em forma gráfica, que podem ser feitas tanto em papel milimetrado (em tamanho grande o suficiente para ser apresentado) quanto em softwares como o Excel. Deve-se apresentar a temperatura e a umidade em função do tempo, e, também, a umidade em função da temperatura, para explorar a pressão de vapor de saturação. A ideia é discutir como as variáveis mudaram com o tempo e se os(as) estudantes notaram o efeito de algum fenômeno anotado na variação encontrada. Em caso de medidas em mais de um local, como explicar a diferença nas medidas? Existe erro instrumental? Qual o efeito do sombreamento das árvores? Com a discussão esperada, o(a) professor(a) deve aproveitar para esclarecer potenciais dúvidas e mediar a atribuição dos resultados com os conceitos vistos em aula.
Caso a compra dos higrômetros seja inviável, são sugeridas duas opções: 1) o uso de dados de temperatura e umidade de várias localidades disponíveis no sítio do INMET (ver seção de links); 2) o uso de dados meteorológicos mostrados nos aplicativos de celular. O intervalo de medidas pode variar para estes casos, ficando o(a) docente responsável por adaptar a atividade, mas com apresentação de gráficos e discussões compatíveis com a proposta usando termo-higrômetro.
Materiais Relacionados
1) Aplicações com número neperiano: vídeo “e (euler’s number) shows up a lot”. Acesso em: 18-08-2019.
2) Sobre a Lei de Dalton das pressões parciais: texto “9.11: Dalton’s Law of Partial Pressures”. Acesso em: 18-08-2019.
3) Aprofundamento teórico para equação de Clausis-Clapeyron: conteúdo “Clausius–Clapeyron relation”. Acesso em: 18-08-2019.
4) Diferentes formas da equação de Clausius-Clapeyron para a pressão de vapor de saturação: conteúdo “Saturation vapor pressure formulations”. Acesso em: 18-08-2019.
5) Para mostrar a umidade relativa média globalmente: conteúdo “Climate Forecast System Reanalysis (CFSR)”. Acesso em: 18-08-2019.
6) Para mostrar a umidade específica média globalmente: site “Reanalysis: Specific Humidity, Temperature, and Wind”. Acesso em: 18-08-2019.
7) Para acesso a dados meteorológicos e climatologias, utilize o site do Instituto Nacional de Meteorologia (INMET).