Conteúdos
– Funções
Objetivos
– Compreender as funções como relações de dependência unívoca entre duas variáveis e suas representações numéricas ou algébricas
– Utilizar o conceito de função para analisar situações que envolvam relações funcionais entre duas variáveis
– Resolver problemas que envolvam o uso de funções de uma variável
1ª Etapa: Início de conversa
As funções compõem um tópico essencial para o estudante terminando o ensino fundamental II e iniciando o ensino médio. As relações de dependência que podem ser expressadas por funções passeiam entre quase todas as disciplinas escolares, incluindo aquelas consideradas ciências humanas.
Funções expressam relações de dependência entre duas variáveis. Essas variáveis podem ser objetos dos tipos mais variados. São exemplos concretos de funções: a relação estabelecida entre a velocidade de um veículo e o tempo de viagem num determinado trajeto ou então, o cálculo da hipotenusa de um triângulo retângulo dados os catetos.
Nesse plano de aula será explorado, por meio de um objeto virtual de aprendizagem (OVA), o conceito de função e os estudantes serão estimulados a manipularem funções de forma a compreenderem como se dá a relação de dependência entre duas variáveis.
2ª Etapa: Objeto Virtual de Aprendizagem - Números
Nessa segunda etapa, os alunos utilizarão o objeto virtual de aprendizagem (OVA) Construtor de Funções, elaborado pela PhET Interactive Simulations. Os alunos devem acessar essa página e clicar no botão de início.

Solicite aos alunos que cliquem em “Números”.
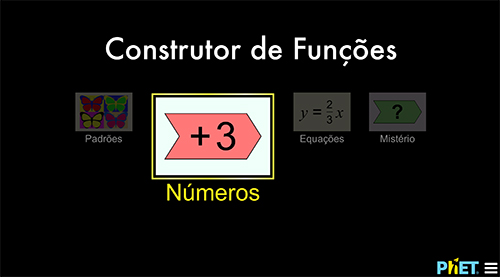
Os alunos serão direcionados para uma página como essa:
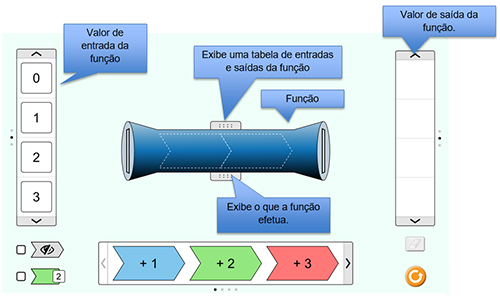
Apresente aos estudantes o funcionamento da ferramenta. Observe na imagem acima como utilizar alguns dos botões.

Na parte inferior da página, estão as peças utilizadas para formar a função desejada no tubo. Os alunos irão a arrastá-las para o tubo, encaixando-as nos espaços correspondentes, formando uma função. Veja um exemplo:
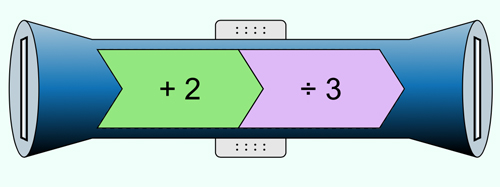
Essa é a função que soma 2 e, em seguida, divide essa soma por três. Solicite aos alunos que façam alguns testes, construindo funções como:
f(x)=x+2;
f(x)=(x+3)÷2;
f(x)=(x-1)×3.
Durante esse experimento é útil conhecer a ferramenta ![]() , que apaga as saídas da função e
, que apaga as saídas da função e ![]() , que reinicia a atividade. Pode ser apropriado aumentar o grau de desafio para alguns estudantes mais avançados. Em dupla, os alunos irão elaborar funções e ativarão a ferramenta
, que reinicia a atividade. Pode ser apropriado aumentar o grau de desafio para alguns estudantes mais avançados. Em dupla, os alunos irão elaborar funções e ativarão a ferramenta ![]() , que exibe ou não as peças encaixadas no tubo da função – para que o outro colega descubra a função envolvida na relação através do uso de diferentes valores de entrada.
, que exibe ou não as peças encaixadas no tubo da função – para que o outro colega descubra a função envolvida na relação através do uso de diferentes valores de entrada.
3ª Etapa: Objeto virtual de aprendizagem - equações
Utilizando a ferramenta ![]() , volte para a página inicial e agora, será solicitado aos alunos que acessem a modalidade de equações.
, volte para a página inicial e agora, será solicitado aos alunos que acessem a modalidade de equações.

Deixe os estudantes explorarem essa opção. Solicite que expressem, utilizando o programa, equações do tipo:
y=-2(x+1);
f(x)=-2(x+1)÷2;
f(x)=-3(x-1)×3.
Novamente, em dupla, peça que elaborem funções e ativem a ferramenta ![]() , que exibe ou não as peças encaixadas no tubo da função – para que o outro colega descubra a função envolvida na relação através do uso de diferentes valores de entrada.
, que exibe ou não as peças encaixadas no tubo da função – para que o outro colega descubra a função envolvida na relação através do uso de diferentes valores de entrada.
4ª Etapa: Finalizando a discussão
Encerre promovendo uma discussão sobre funções e seus usos em matemática. Peça à alguns estudantes que expressem em palavras o que é uma função. Além dos exemplos matemáticos, desafie-os a elaborarem funções que relacionem duas grandezas não matemáticas.
Materiais Relacionados
1) O(A) professor(a) poderá recordar os conceitos fundamentais do conteúdo na seguinte obra: IEZZI, Gelson et al. Fundamentos de Matemática Elementar: Conjuntos e Funções, volume 1. São Paulo: Atual Editora, 2004.
2) Poderá acessar a página “O que é função?” para uma rápida retomada sobre o assunto.
3) Será utilizada a plataforma da PhET Interactive Simulations. É importante conhecer a proposta dessas simulações antecipadamente, acessando seu endereço.