Conteúdos
– Combinatória
– Princípio fundamental da contagem
– Estudo de possibilidades
– Estatística
Objetivos
– Aplicar o princípio fundamental da contagem em situações problemas
– Estudar as possibilidades de formações de grupos da Copa do Mundo
– Estudar um modelo de resoluções de problemas de combinatória
– Estudar aplicações de estudos de possibilidades em situações de sorteio
1ª Etapa: Início de conversa
Durante os meses que antecedem a Copa do Mundo, há expectativas acerca do evento, sobre os países classificados, sobre os jogadores convocados e, também, sobre os grupos que serão formados para a primeira rodada de jogos do torneio. Há uma grande torcida esperando que a seleção brasileira não encare, logo na primeira rodada, as seleções consideradas “fortes”. Com toda essa expectativa, o (a) professor (a) poderá aproveitar o tema para fazer um estudo de possibilidades.
A contagem de possibilidades faz uso de tabelas, diagramas, raciocínio multiplicativo e pode gerar boas conclusões sobre padrões na resolução desse tipo de situação problema. Os alunos poderão observar que a resolução se dá por meio de multiplicações, com algumas exceções, e terão contato com uma base muito importante do estudo de estatística.
Para iniciar a conversa o (a) professor (a) poderá utilizar uma tabela de grupo de qualquer Copa do Mundo e perguntar o que os alunos conhecem sobre os critérios e procedimentos do sorteio de grupos realizado pela FIFA. Nesse momento, o (a) professor (a) deverá estar atento a possíveis equívocos sobre o procedimento real, esclarecendo dúvidas e ajudando os alunos a formular possíveis hipóteses sobre esse evento.
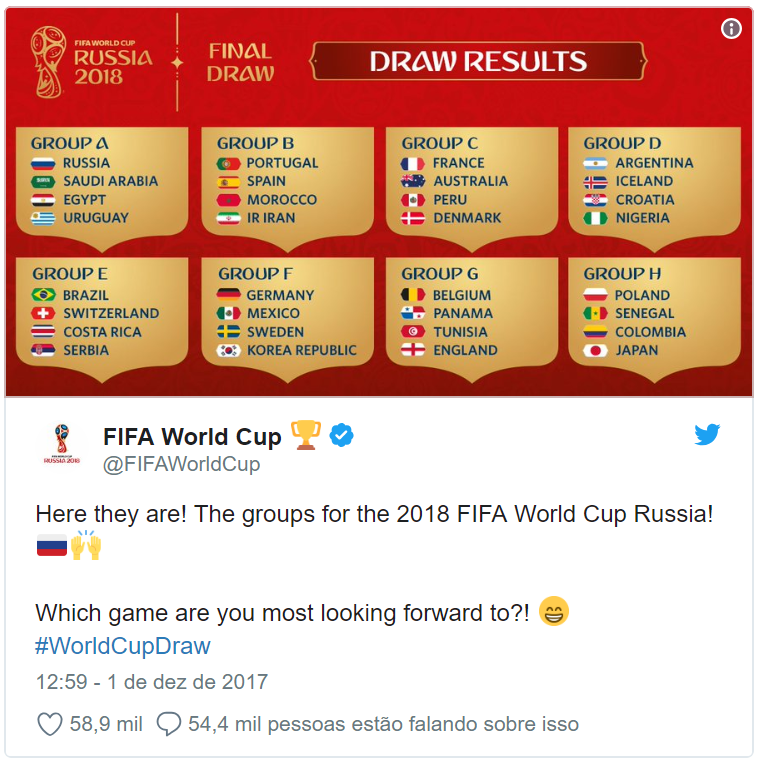
2ª Etapa: Um estudo de possibilidades de formação de grupos
Por se tratar de um fenômeno aleatório, ou seja, uma experiência cuja realização depende do acaso, é muito comum pessoas relacionarem o resultado de um sorteio a algo bem sucedido, obtido com sorte, ou mal sucedido, se obtido com azar. Para conclusões desse tipo, muitas variáveis são consideradas e, provavelmente, os alunos comentarão sobre as seleções e jogadores que tiveram melhores e piores desempenhos e as chances do Brasil ser campeão. Nessa etapa, o(a) professor(a) poderá aproveitar a discussão e convidar os alunos a calcularem as possibilidades de grupos que podem ou poderiam ser formados a partir dos potes de sorteio da Copa do Mundo.
O (A) professor (a) poderá usar qualquer quantidade de 32 seleções, sendo ela de um evento hipotético ou outro já ocorrido. Vamos analisar as 32 seleções da Copa de 2018 e os quatro potes do sorteio da FIFA:
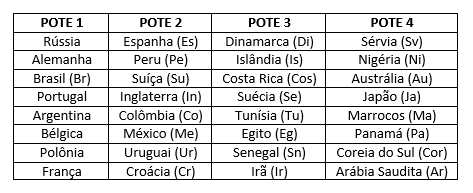
As seleções do POTE 1 são as cabeças de chave de cada grupo, ou seja, cada uma estará em um grupo diferente, não podendo se enfrentar na primeira rodada de jogos. Sendo assim, na Copa de 2018, o Brasil foi o primeiro do seu grupo (Grupo E) a ser selecionado.
Vamos analisar, individualmente, o caso do Brasil:
Sabemos que o grupo do Brasil deve ser formado com mais uma seleção do POTE 2, uma do POTE 3 e uma do POTE 4. Então, vamos contar quantos grupos são possíveis formar com essa regra:
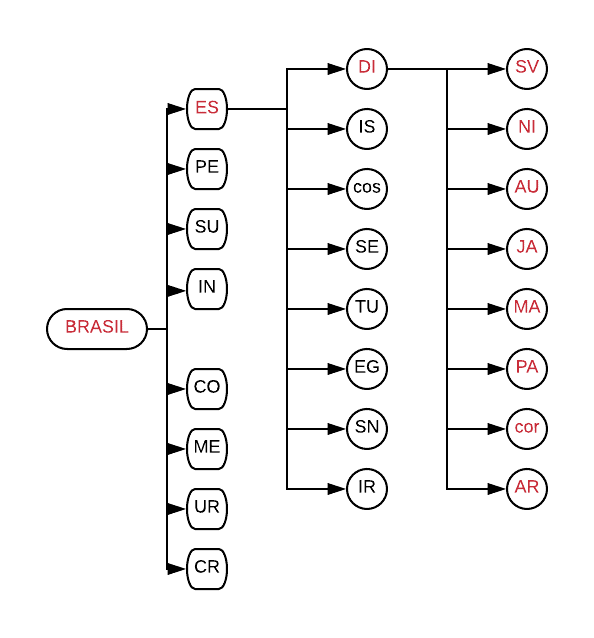
O (A) professor (a) poderá construir parte do diagrama de árvore com os alunos, de modo que eles possam concluir que:
• variando apenas as seleções do POTE 4, há 8 possibilidades de grupos que contenham Brasil, Espanha e Dinamarca.
• variando as seleções do POTE 3 E 4, há 64 possibilidades de grupos que contenham Brasil e Espanha.
• variando as seleções do POTE 2, 3 E 4, há 512 possibilidades de grupos que contenham o Brasil.
Nessa etapa, o objetivo é ajudar os alunos a criarem estratégias para conseguirem chegar nesses números. A contagem poderá ser feita no início, porém, depois, com a ajuda do (a) professor (a), os alunos deverão investigar possíveis padrões de resoluções.
3ª Etapa: Sistematizando resoluções
Para que o aluno consiga encontrar um padrão na resolução desse tipo de problema, o (a) professor (a) deverá mediar investigações sobre a contagem de possibilidades dos grupos formados pelas outras seleções cabeça de chave, de modo que o aluno consiga perceber que:
– há apenas 1 possibilidade para a primeira seleção, a cabeça de chave do grupo;
– para cada seleção, há 8 possibilidades do POTE 2;
– para cada par de seleção obtidas dos POTES 1 E 2, há 8 possibilidades de sorteio para a terceira seleção (POTE 3);
– por último, para cada três seleções escolhidas, há 8 possibilidades de sorteio para a quarta seleção.
isso significa um total de 1×8×8×8=512 possibilidades de grupos da seleção cabeça de chave.
Ou seja, se são convocadas 32 seleções para participar do campeonato, há 512 possibilidades de grupos da primeira rodada de jogos para cada seleção cabeça de chave da Copa do Mundo FIFA.
Materiais Relacionados
1 – Para entender sobre os quatro potes do sorteio dos grupos da Copa do Mundo, leia o artigo: “Fifa define divisão das seleções nos potes para sorteio de grupos da Copa de 2018”.
2 – Para conferir a cobertura do sorteio dos grupos, leia a reportagem “Sorteio da Copa do Mundo Rússia 2018: veja como ficaram os grupos”.
3 – Leia o texto: “Combinação na árvore de possibilidades”.

