Conteúdos
Este plano de aula de física trata do conceito de centro de massa (CM). Inicialmente, faz-se uma discussão introdutória, destacando a importância de tal conceito no estudo dos movimentos dos corpos rígidos. Na 2ª etapa, apresenta-se a expressão matemática utilizada para o cálculo do centro de massa de um sistema de partículas. De forma qualitativa, os centros de massa de algumas figuras geométricas planas são apresentados na 3ª etapa. Alguns exemplos resolvidos são discutidos na última etapa, visando a consolidação do conteúdo. O material também conta com algumas sugestões de textos e vídeos (em “Materiais relacionados”), para que o/a professor/a possa buscar um maior aprofundamento sobre o assunto.
● Introdução ao tema;
● Cálculo do centro de massa;
● Centro de massa de figuras geométricas planas; e
● Exemplos de cálculo do centro de massa.
Objetivos
● Compreender o que é o centro de massa de um corpo e de um sistema de partículas;
● Conhecer o centro de massa de algumas figuras geométricas planas; e
● Aprender a calcular o centro de massa de alguns sistemas de partículas.
Ensine também:
Primeira Lei de Newton: explique o conceito de inércia aos alunos
Palavras-chave:
Centro de massa. Eixo de simetria.
Previsão para aplicação:
4 aulas (50 min./aula)
1ª Etapa: Introdução ao tema
Acesso em: 15 de março de 2022.
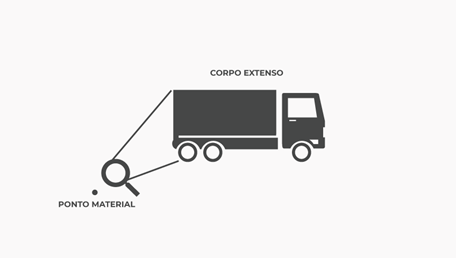
Em física, ao estudarmos os movimentos dos corpos e suas causas, dependendo do grau de complexidade que se queira atribuir a uma determinada análise, faz-se necessário considerar algumas simplificações. Por exemplo, ao tratarmos de corpos rígidos em movimento, não raramente desconsideramos as suas dimensões físicas (altura, largura e profundidade), passando, assim, a considerá-lo como um ponto material. E isso só é possível graças a um conceito chave: o centro de massa.
O centro de massa de um corpo é um ponto (fictício) sobre o qual é possível considerar que toda a sua massa está concentrada, o que nos permite tratá-lo como um ponto material (ou partícula pontual). A localização desse ponto depende, naturalmente, da massa do corpo, bem como de sua forma geométrica, ou seja, depende da forma como a massa do corpo está distribuída.
Tal definição de centro de massa aplica-se não apenas para um corpo rígido, podendo ser estendida para um sistema formado por N partículas (ou seja, formado por corpos separados). Dessa forma, o centro de massa de um sistema de N partículas é um ponto sobre o qual podemos considerar que a massa total (a soma das massas das N partículas) do sistema está concentrada.
Corpos que possuem uma distribuição homogênea de massa apresentam uma característica interessante: seus centros geométricos coincidem com os seus centros de massas. Entretanto, vale mencionar que nem sempre o centro de massa de um corpo está localizado dentro dele.
1 – De fato, o centro de massa de alguns corpos encontra-se em regiões do espaço onde não existe massa. Exemplo: o centro de massa de um anel está localizado no centro da circunferência que ele descreve, e nesse local não existe nenhuma massa do anel.
2ª Etapa: Cálculo do centro de massa
Nesta etapa, veremos a definição matemática de centro de massa.
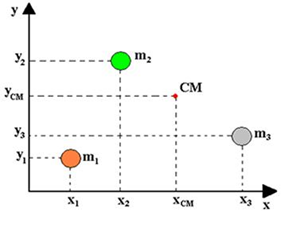
Consideremos um sistema formado por 3 partículas: P_1,P_2 e P_3, distribuídas sobre o mesmo plano cartesiano, cujo eixo vertical é y (ordenada) e o eixo horizontal é x (abscissa), como mostra a figura a seguir:
Acesso em: 15 de março de 2022.
A partícula P_1 possui como coordenadas os pontos (x_1,y_1 ) e massa m_1; a partícula P_2 possui como coordenadas os pontos (x_2,y_2 ) e massa m_2; e a partícula P_3 possui como coordenadas os pontos (x_3,y_3 ) e massa m_3. Por meio das médias ponderadas, podem ser obtidas as coordenadas do centro de massa (CM) desse sistema de partículas:
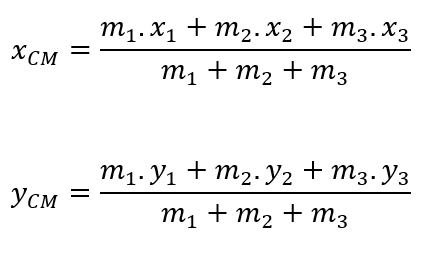
No caso de um sistema formado por N partículas, distribuídas sobre o mesmo plano cartesiano, para encontrar as coordenadas do centro de massa (CM) de tal sistema, basta generalizar as expressões para os cálculos de x_CM e y_CM, da seguinte maneira:
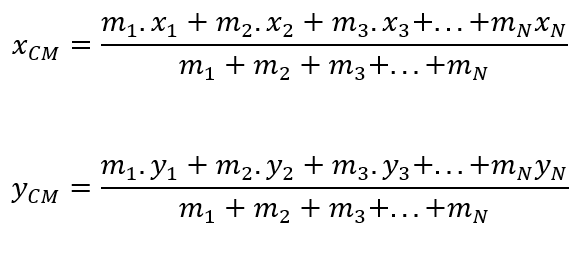
3ª Etapa: Centro de massa de figuras geométricas planas
Para encontrarmos o centro de massa de figuras geométricas planas homogêneas ² , podemos utilizar o conceito de eixo de simetria.
Em geometria, o eixo de simetria é uma linha que divide um corpo em duas partes “espelhadas”, ou seja, uma linha que divide o corpo (figura) em duas partes simétricas, ou iguais.
O eixo de simetria é um conceito bastante importante, pelo fato do centro de massa de uma determinada figura plana sempre estar localizado sobre tal eixo. Para o caso de figuras planas que possuem mais de um eixo de simetria, o centro de massa de tais figuras localiza-se na intersecção dos seus eixos de simetria.
Vejamos agora alguns exemplos de figuras geométricas planas ³ homogêneas e seus centros de massa, obtidos por meio do conceito de eixos de simetria:
1) Retângulo
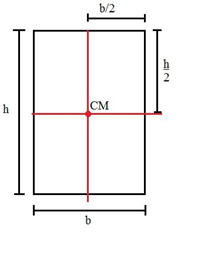
Consideremos um retângulo de base b e altura h. Tal figura possui dois eixos de simetria (linhas vermelhas), e o seu centro de massa está localizado na intersecção entre esses eixos.
2 – Homogênea aqui está relacionada ao fato de a distribuição de massa ser constante, ou seja, a densidade é constante.
3 – O/A professor/a pode elaborar uma atividade prática para a turma fazer com tais figuras, utilizando apenas folhas A4, papelão, tesoura sem ponta, compasso, régua e lápis (ou caneta). Pode-se pedir para que a turma se divida em grupos, em que cada um ficará responsável por confeccionar uma das figuras. Posteriormente, cada grupo deve encontrar o centro de massa da sua figura. Após encontrar o centro de massa das figuras, um desafio interessante é pedir para cada grupo tentar equilibrá-las na ponta de um lápis ou caneta.
Acesso em: 15 de março de 2022.
Como mostra a figura, o eixo de simetria vertical divide a sua base b pela metade, e o eixo de simetria horizontal divide a sua altura h também pela metade. Dessa forma, temos que a localização do centro de massa (CM) de um retângulo está no ponto:
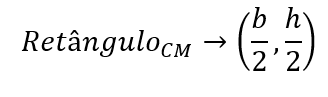
2) Círculo
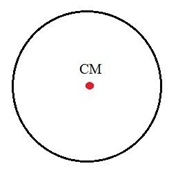
O centro de um círculo é um ponto que está equidistante de todos os pontos delimitados por uma circunferência. Essa distância (que não muda) do centro do círculo até a sua “borda” (circunferência) é o que chamamos de raio do círculo. Naturalmente, tem-se que o círculo possui infinitos eixos de simetria, todos eles passando pelo seu centro, logo, o centro de massa de um círculo localiza-se nesse ponto (centro do círculo).
Acesso em: 15 de março de 2022.
3) Triângulo equilátero
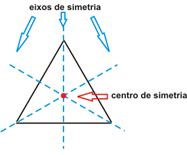
Um triângulo equilátero é uma figura geométrica plana que possui os seus três lados iguais. Ele possui três eixos de simetria (linhas tracejadas em azul), que podem ser obtidos a partir das suas bissetrizes, ou seja, a partir das semirretas que partem de seus vértices, dividindo os seus ângulos internos em duas partes com a mesma medida (em dois ângulos congruentes). Novamente, no ponto de intersecção entre os seus três eixos de simetria, localiza-se o seu centro de massa (que coincide com o seu centro de simetria), como mostra a figura a seguir:
Acesso em: 15 de março de 2022
4ª Etapa: Alguns exemplos de cálculo do centro de massa
Exemplo 01: Determine as coordenadas do centro de massa do sistema de partículas a seguir.
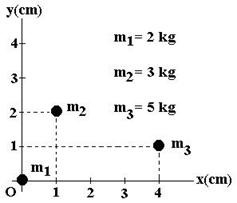

De posse desses dados, podemos encontrar as coordenadas do centro de massa desse sistema de partículas, utilizando as seguintes expressões:
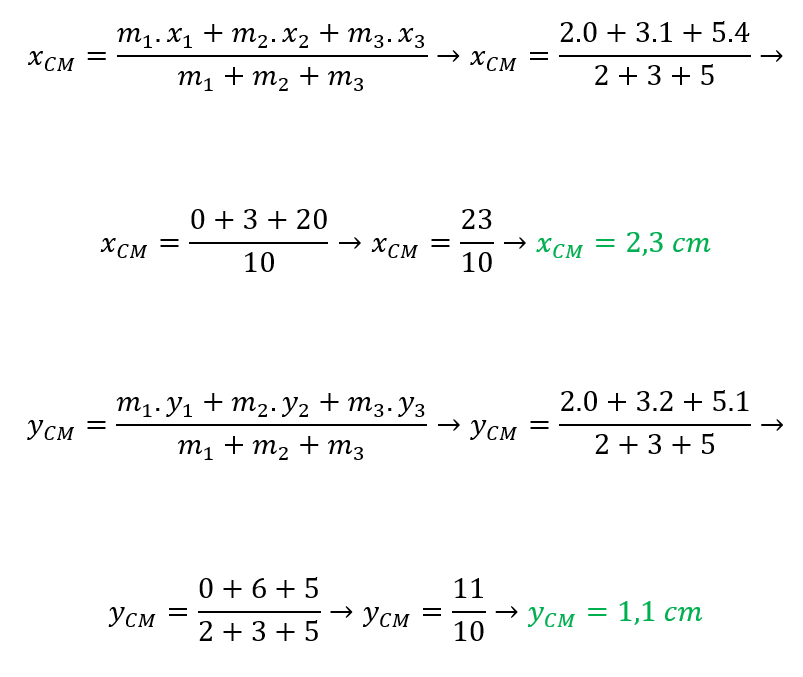
Portanto, as coordenadas do centro de massa do sistema de partículas são:
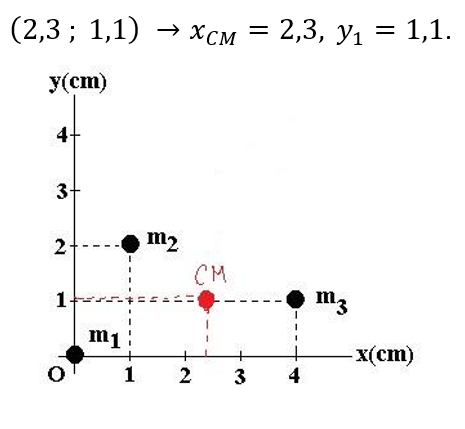
Exemplo 02: A distância entre o centro da Terra e o centro da Lua mede 3,8×10^5 km. A massa da Terra é 82 vezes maior que a massa da Lua. A que distância do centro da Terra encontra-se o centro de massa do sistema Terra-Lua.
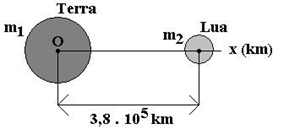
Resolução:
Adotaremos um eixo x passando pelos centros da Terra e da Lua, com origem no centro da Terra.
Nestas condições, a abscissa (x) do centro de massa da Terra é nula (x_1=0) e a abscissa da Lua é x_2=3,8×10^5 km. Como o problema pode ser tratado considerando-se apenas o eixo x, significa que o centro de massa do sistema Terra-Lua será localizado sobre tal eixo, dessa forma, a ordenada (y) do centro de massa de tal sistema será nula (y_CM=0). Como o enunciado do exemplo e a figura nos informa, tem-se que a massa da Lua é m_2, enquanto a massa da Terra m_1 é 82 vezes a massa da Lua, ou seja, m_1=82m_2. De posse desses dados, podemos calcular a abscissa (x_CM ) do centro de massa do sistema Terra-Lua, da seguinte maneira:

Plano de aula elaborado pelo professor Elves Silva Moreira.
Coordenação Pedagógica: prof.ª Dr.ª Aline Monge.
Materiais Relacionados
● Para ler conteúdos sobre centro de massa:
UFABC – Centro de massa
Acesso em: 27 de fevereiro de 2022.
Mundo Educação
Acesso em: 27 de fevereiro de 2022.
InfoEscola
Acesso em: 27 de fevereiro de 2022.
Acesso em: 27 de fevereiro de 2022.
● Para ver vídeos sobre centro de massa:
Centro de massa – Professor da USP Explica
Acesso em: 27 de fevereiro de 2022.
09 – Centro de massa – Física com Filgueira
Acesso em: 27 de fevereiro de 2022.
Sistemas de partículas – Posição do Centro de massa – Responde Aí
Acesso em: 27 de fevereiro de 2022.

