Conteúdos
Este plano de aula de matemática apresenta o conceito de arranjo simples e com repetição. O material aborda a análise combinatória, bem como a importância dos conceitos do Princípio Fundamental da Contagem (PFC) e do fatorial de um número natural, para se estudar os problemas tratados em análise combinatória. Após uma breve recordação do que é uma permutação simples e com repetição, o conceito de arranjo simples é apresentado, com a discussão de alguns exemplos resolvidos. Finaliza-se o material com uma breve apresentação do conceito de arranjo com repetição, em que um dos exemplos resolvidos na etapa anterior é refeito, com as devidas considerações. O material também conta com algumas sugestões de textos e vídeos (em “Materiais Relacionados”) para que o/a professor/a possa buscar um aprofundamento no assunto.
● Análise combinatória;
● Permutação;
● Arranjo simples; e
● Arranjo com repetição.
Objetivos
● Compreender do que trata a análise combinatória;
● Compreender que a permutação simples é um caso particular de arranjo simples; e
● Compreender o que é um arranjo simples e um arranjo com repetição, e aprender a
trabalhar matematicamente com tais conceitos.
Ensine também
Função modular: representação gráfica
Inequação de 1º grau: significado e exercícios
Palavras-Chave:
Análise combinatória. Permutação. Arranjo simples. Arranjo com repetição.
Previsão para aplicação:
4 aulas (50 min/aula).
1ª Etapa: Análise combinatória
Em matemática, diversos problemas envolvendo a contagem de situações possíveis e específicas, contagem de combinações de elementos de um determinado conjunto etc., são bastante corriqueiros. A área da matemática responsável pelo estudo e desenvolvimento de técnicas para tratar de tais tipos de problemas é a análise combinatória.
No estudo da análise combinatória, destaca-se a importância do Princípio Fundamental da Contagem (PFC). O PFC consiste num método que pode ser utilizado para calcular a quantidade de combinações possíveis em uma situação específica.
Exemplo: Albert possui 3 bonés e 5 camisas. Sabendo que Albert sempre sai de casa com um boné e com uma camisa, de quantas maneiras distintas ele pode se vestir?
Resolução: Utilizando o PFC, basta multiplicarmos cada uma de suas opções:
3 (bonés) ×5 (camisas)=15 “looks” distintos
Dessa forma, com 5 camisas e 3 bonés, Albert tem 15 possibilidades de “looks” distintos.
Outro conceito bastante importante para o estudo da análise combinatória é o fatorial de um número natural. O fatorial de um número natural n (cuja notação é n!) consiste em uma operação matemática em que multiplicamos um determinado número n por todos os seus antecessores naturais até o número 1, ou seja:
n!=n×(n-1)×(n-2)×(n-3)…3×2×1,para n≥2
Da própria definição (convenção) de fatorial de um número natural, tem-se que:
0!=1
1!=1
Munidos do Princípio Fundamental da Contagem (PFC) e do conceito de fatorial de um número natural, somos capazes de resolver diversos problemas tratados em análise combinatória.
2ª Etapa: Permutação
Em análise combinatória, certos padrões são exibidos em determinados tipos de problemas, de forma que se desenvolveu métodos específicos para tratar de problemas de mesma natureza.
Ao se analisar determinados tipos de agrupamentos (combinações) tratados em análise combinatória, nota-se que se trata de situações com permutação simples. Para encontrar a permutação simples de um número natural n, basta calcular o fatorial desse mesmo número n, ou seja:

Naturalmente, há casos em que a permutação envolve elementos repetidos. Assim, o número de combinações possíveis em uma permutação com n elementos, onde n_1 e n_2 elementos estão repetidos, pode ser calculada a partir da seguinte expressão matemática:

3ª Etapa: Arranjo simples
Consideremos um determinado conjunto formado por n elementos, em que se pretende agrupar p elementos desse mesmo conjunto de maneira que a posição de cada elemento p importe (onde p≤n). Ao efetuarmos tal tarefa, em que a totalidade dos agrupamentos possíveis são formados com p elementos que não se repetem, estamos tratando de um arranjo simples.
A expressão matemática para o cálculo da totalidade de arranjos simples possíveis de n elementos, tomados de p em p elementos, é a seguinte:

Observação: Ao tratarmos de arranjos simples, a ordem dos elementos agrupados é importante. Existe um certo tipo de agrupamento, também tratado em análise combinatória, em que a ordem dos elementos não importa: a combinação simples.
Vejamos agora um exemplo, de forma que possamos resolvê-lo intuitivamente:
Exemplo 1: Consideremos um conjunto formado pelas três primeiras letras do alfabeto grego (α,β,γ). De quantas maneiras diferentes podemos escolher duas letras gregas desse mesmo conjunto, para o caso em que a ordem das letras é relevante?
Lembrete:
α: 1ª letra do alfabeto grego → Alfa;
β: 2ª letra do alfabeto grego →Beta;
γ: 3ª letra do alfabeto grego →Gama.
Temos que:
Com α e β{1º agrumamento →(α,β) 2º agrupamento →(β,α)
Com α e γ{ 3º agrumamento →(α,γ) 4º agrupamento →(γ,α)
Com β e γ{ 5º agrumamento →(β,γ) 6º agrupamento →(γ,β)
Portanto, conclui-se que podemos formar 6 (seis) agrupamentos com as três primeiras letras do alfabeto grego, tomadas de duas em duas letras. No entanto, por se tratar de um arranjo simples, também podemos resolver esse exemplo com a seguinte expressão matemática:
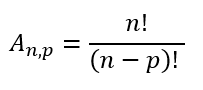
Identificamos que o conjunto em questão possui 3 elementos (letras), logo: n=3.
E identificamos que a quantidade de elementos (letras) por agrupamento é 2, logo: p=2.
Assim, temos:
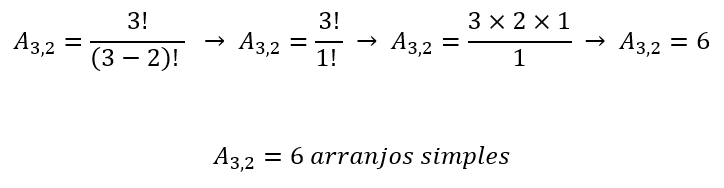
Exemplo 2: A biblioteca de uma universidade disponibiliza armarinhos para que os/as usuários/as possam guardar mochilas e outros objetos. Ao todo, existem 300 armarinhos disponíveis. O cadeado de cada armarinho possui 4 rodelas numeradas de 0 a 9. Marque a alternativa correta:
a) Existem mais armarinhos do que a quantidade possível de senhas sem algarismos repetidos.
b) Existe uma maior quantidade de senhas possíveis sem algarismos repetidos do que armarinhos.
c) A quantidade de armarinhos é igual à quantidade de senhas possíveis sem algarismos repetidos.
Resolução:
Primeiramente, precisamos encontrar a quantidade possível de senhas, sem algarismos repetidos, para esse tipo de cadeado.
Podemos resolver este problema utilizando o Princípio Fundamental da Contagem (PFC). Como cada rodela é numerada de 0 a 9, temos 10 possibilidades de escolha para a primeira rodela. Ao escolhermos um algarismo para a primeira rodela, resta-nos 9 possibilidades de escolha para a segunda rodela, pois estamos interessados apenas em senhas que não possuam algarismos repetidos. Como já escolhemos dois algarismos, resta-nos 8 possibilidades de escolha para a terceira rodela. Finalmente, para a quarta e última rodela, resta-nos apenas 7 possibilidades de escolha. Dessa forma, podemos fazer o seguinte produto entre todos os fatores que acabamos de identificar para cada uma das quatro rodelas:
10×9×8×7=5040 senhas possíveis,sem algarismos repetidos
Naturalmente, por se tratar das senhas possíveis para um determinado tipo de cadeado, este problema trata de uma situação em que a posição de cada elemento (algarismo) importa. E, por se tratar de senhas que não possuem algarismos repetidos, temos aqui um caso de arranjo simples. Dessa forma, podemos utilizar a expressão matemática correspondente, para o caso de um conjunto formado por 10 elementos, tomados de 4 em 4:

Como temos 300 armarinhos, e 5040 possibilidades de senhas sem algarismos repetidos, a alternativa correta é a letra b.
Neste momento, vale destacar a seguinte situação:
Quando temos um conjunto formado por n elementos, tomados de n em n, ou seja, quando a quantidade de elementos possíveis é igual à quantidade de elementos por agrupamento, n = p, obtemos:

4ª Etapa: Arranjo com repetição
Para o caso de um conjunto constituído por n elementos, agrupados de forma ordenada de p em p elementos desse mesmo conjunto, mas que permite repetições, tem-se, naturalmente, o arranjo com repetição, também conhecido como arranjo completo. A expressão matemática para o arranjo com repetição é a seguinte:

Agora, vamos refazer o Exemplo 2 da etapa anterior, considerando-o da seguinte maneira:
Exemplo 2*: A biblioteca de uma universidade disponibiliza armarinhos para que os/as usuários/as possam guardar mochilas e outros objetos. Ao todo, existem 300 armarinhos disponíveis. O cadeado de cada armarinho possui 4 rodelas numeradas de 0 a 9. Quantas possibilidades de senhas existem, para o caso em que a repetição dos algarismos é permitida?
Resolução:
Novamente, podemos utilizar o Princípio Fundamental da Contagem (PFC).
Tem-se que, para a primeira rodela, existem 10 algarismos possíveis de serem escolhidos. Para a segunda rodela, existem 10 algarismos disponíveis também, posto que podemos escolher o mesmo algarismo da primeira rodela. E o mesmo vale para a terceira e para a quarta rodela. Dessa forma, o número de senhas possíveis para este caso é o seguinte produto:
10×10×10×10=10 000 senhas possíveis
Podemos resolver este problema de outra forma. Este caso trata exatamente de um arranjo com repetição, ou seja, de um arranjo completo.
Identificamos que o conjunto em questão possui 10 elementos (os algarismos de 0 a 9), logo: n=10.
E identificamos que a quantidade de elementos (algarismos) por agrupamento é 4, logo: p=4.
Substituindo na expressão matemática, temos:
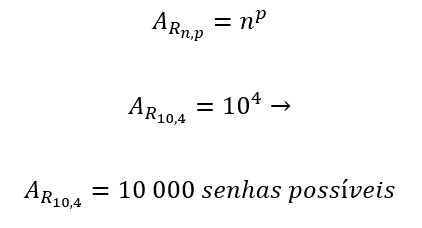
Dessa forma, tem-se que, ao permitirmos senhas com algarismos repetidos, o número de possibilidades de senhas é quase o dobro do número de senhas possíveis sem algarismos repetidos.
Plano de aula elaborado pelo Professor Elves Silva Moreira.
Revisão textual: Professora Daniela Leite Nunes.
Coordenação pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.
Materiais Relacionados
● Para ler conteúdos sobre arranjo simples e com repetição:
Brasil Escola – Arranjo simples
Acesso em: 24 de setembro de 2022.
Info Escola – Arranjo simples
Acesso em: 24 de setembro de 2022.
Quero Bolsa
Acesso em: 24 de setembro de 2022.
Brasil Escola – Arranjo com repetição
Acesso em: 24 de setembro de 2022.
● Para ver vídeos sobre arranjo simples e com repetição:
Arranjo Simples – Professora Angela Matemática
Acesso em: 24 de setembro de 2022.
Arranjo com repetição – Brasil Escola
Acesso em: 24 de setembro de 2022.

