Conteúdos
– Álgebra e expressões algébricas
– Cálculo de área de triângulos e quadriláteros
– Unidades de medidas de comprimento e área
– Equação do 1º grau
Objetivos
– Conhecer aplicações das planilhas eletrônicas
– Reforçar os conceitos de cálculo de área de figuras planas
– Utilizar instrumentos de medição (régua e transferidor)
– Revisar os conteúdos de equação do 1º grau
Previsão para aplicação:
4 aulas (50 min/aula)
1ª Etapa: Introdução ao tema
A Álgebra é um dos grandes campos da Matemática e é estudada em todos os anos do Ensino Fundamental em suas diversas subáreas, como por exemplo: equações, funções, fórmulas, propriedades etc. As planilhas eletrônicas (sendo Excel a mais conhecida) possuem diversas utilidades e são largamente usadas no mundo do trabalho. Abordar a Álgebra através das planilhas eletrônicas, além de reforçar conteúdos vistos, contribui para que os estudantes aprendam a usar uma importante ferramenta.
Nesta proposta, iremos abordar como planilhas eletrônicas podem ser utilizadas para revisar as fórmulas para cálculo de área de triângulos e quadriláteros, e a resolução de equações do 1º grau. Devido ao conteúdo, o plano de aula é mais indicado para alunos do 8º ano, mas pode ser adaptado para diversos outros temas e séries.
Talvez seja necessária uma aula introdutória sobre conceitos básicos de como usar planilhas eletrônicas, para nivelar o conhecimento de todos.
2ª Etapa: Calculando área de triângulos
Os alunos podem se organizar em duplas ou trios. Cada grupo deverá ter acesso a um computador com software de planilha eletrônica instalado e receberá quatro triângulos numerados feitos de cartolina, como os que seguem abaixo:
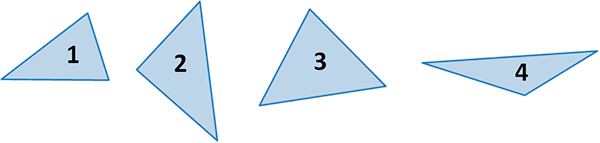
Cada triângulo deve ter medidas e ângulos internos distintos. Utilizando instrumentos de medição (régua e transferidor), os alunos devem fazer medições com o intuito de calcular a área de cada polígono. Em seguida, deverão construir a seguinte tabela na planilha eletrônica:
| A | B | C | D | |
|---|---|---|---|---|
| 1 | Tabela de triângulos | |||
| 2 | Triângulo | base b | altura h | Área A |
| 3 | Triângulo 1 | |||
| 4 | Triângulo 2 | |||
| 5 | Triângulo 3 | |||
| 6 | Triângulo 4 | |||
Na coluna B deverão colocar as medidas das bases, e na coluna C deverão colocar as medidas das alturas. Os alunos terão autonomia para definirem estratégias de medição e qual unidade de medida usar, pode ser em milímetros, centímetros (mais indicadas) ou até mesmo em metros. Interessante que eles indiquem nos desenhos as medidas encontradas.
Nas células da coluna D os estudantes devem inserir fórmulas que irão fazer referência às colunas B e C. Nesse momento a álgebra estará presente, visto que as fórmulas conterão equações literais, cujos valores podem variar. Na célula D3, por exemplo, devem escrever “=(B3*C3)/2”.
Após finalizada a tabela, o(a) professor(a) pode iniciar um debate com a turma a respeito das respostas; chamar a atenção sobre como os valores da coluna D variam de acordo com os valores das colunas B e C; fazer uma discussão sobre as unidades de medidas utilizadas e verificar se há compatibilidade das unidades de comprimento (mm, cm, m) com as unidades de área (mm², cm², m²). Por fim, se houver tempo, poderão debater outras formas de calcular área de triângulos, e como ficaria a tabela nesses outros casos. Há uma forma, por exemplo, que necessita da medição de um dos ângulos internos, o que possibilita o uso do transferidor.
3ª Etapa: Calculando área de quadriláteros
Nesta etapa, cada grupo receberá quatro quadriláteros distintos (dentre quadrados, retângulos, trapézios, losangos e paralelogramos), feitos de cartolina e numerados, como os que seguem abaixo:

No exemplo, utilizamos um paralelogramo, um retângulo um losango e um trapézio. Utilizando instrumentos de medição (régua e transferido), os alunos devem fazer medições com o intuito de identificar o tipo de quadrilátero e calcular a área de cada polígono. Em seguida, deverão construir a seguinte tabela na planilha eletrônica:
| A | B | C | D | |
|---|---|---|---|---|
| 1 | Tabela de quadriláteros | |||
| 2 | Quadrilátero | medida a | medida b | medida c |
| 3 | Quadrilátero 1 | |||
| 4 | Quadrilátero 2 | |||
| 5 | Quadrilátero 3 | |||
| 6 | Quadrilátero 4 | |||
Como há formas distintas de calcular a área em cada quadrilátero, deverão indicar nas cartolinas quais são as medidas a e b. De forma análoga ao que foi feito com os triângulos, nas células da coluna D os estudantes devem inserir fórmulas que irão fazer referência às colunas B e C. Nesse caso, as fórmulas vão apresentar variações.
Após finalizada a tabela, o(a) professor(a) pode, assim como na etapa anterior, realizar um debate com a turma a respeito da atividade realizada, problematizando possíveis variações.
4ª Etapa: Resolvendo equações de 1º grau
Na etapa final, os alunos irão resolver um problema que envolve equação do 1º grau. Inicialmente, o(a) professor(a) deve apresentar a fórmula que, a partir do comprimento p (em centímetros) do pé, define a numeração N do calçado. Segue:
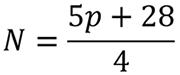
A atividade consiste em montar a tabela abaixo em uma planilha eletrônica e, em seguida, completar com as dimensões dos pés dos componentes do grupo na coluna B.
| A | B | C | |
|---|---|---|---|
| 1 | Tabela – Número calçado | ||
| 2 | Aluno | comprimento p | número N |
| 3 | |||
| 4 | |||
| 5 | |||
Em seguida, na coluna C deverão inserir a fórmula que a partir do número inserido na coluna B calcula o número do calçado. No caso da célula C3, o resultado seria: “=(5*B3 +28)/4”. Para finalizar, pode-se debater com a turma se os resultados encontrados correspondem aos números de calçados que usam.
Materiais Relacionados
1) O(A) professor(a) poderá recordar os conceitos fundamentais de equações e cálculo de áreas nos seguintes conteúdos do site Brasil Escola:
O que é equação?
Área de uma Região Triangular
Área do paralelogramo
2) O(A) professor(a) poderá aprofundar o conteúdo nas seguintes obras:
IEZZI, Gelson et al. Fundamentos de Matemática Elementar: Complexos, Polinômios e Equações. Volume 6. São Paulo: Atual Editora, 2004.
DOLCE, Osvaldo & POMPEO, Nicolau. Fundamentos de Matemática Elementar: Geometria Plana. Volume 9. São Paulo: Atual Editora, 2004.
3) Para conhecer os recursos da planilha eletrônica:
Curso Excel 2016 Básico. Acesso em: 13 de setembro de 2019.

