Conteúdos

Este roteiro de estudos de matemática tem como objetivo definir o que é um círculo trigonométrico e explicar qual sua relevância no estudo da trigonometria, área fundamental de estudo da matemática. Após a indicação de leitura, algumas questões sobre o conteúdo sugerido são apresentadas, visando uma maior fixação. O material conta com uma sugestão de vídeo, possibilitando maior aprofundamento do tema. Na última etapa, há alguns exercícios resolvidos.

Objetivos

• Compreender o que é um círculo trigonométrico;
• Estudar quais são os quadrantes do círculo trigonométrico; e
• Resolver exercícios de aplicação.

Conteúdos / Objetos do conhecimento:

• Círculo trigonométrico.

Palavras-chave:

Círculo trigonométrico. Trigonometria. Seno. Cosseno. Tangente.

Proposta de estudos:

O objetivo deste material é apoiar os alunos na compreensão acerca do que é um círculo trigonométrico e como ele se aplica no estudo da trigonometria. Com isso, é possível aprofundar os conhecimentos sobre funções trigonométricas.

Explore os materiais fornecidos como base, atentando-se para as respostas a cada pergunta orientadora. Durante a leitura, tome nota de quaisquer dúvidas adicionais que venham a surgir, aproveitando para praticar as questões em seu caderno. Após os estudos, escreva um breve resumo com os principais conceitos aprendidos e resolva as questões propostas.

1ª Etapa: Introdução ao círculo trigonométrico

Leia o texto disponível em: Estratégia Vestibulares
Acesso em: 11 de julho de 2024

A partir da leitura do texto acima, responda às seguintes perguntas:

1) O que é e para que serve o círculo trigonométrico?

2) Em quantos quadrantes o círculo trigonométrico é dividido e qual é o ângulo em cada quadrante?

Para saber mais, assista: Círculo Trigonométrico
Acesso em: 11 de julho de 2024.

Gabarito:

1) O círculo trigonométrico é uma figura circular com raio padrão igual a 1. Ele é caracterizado por dois diâmetros que se cruzam, dividindo-o em quatro quadrantes, cada um com um ângulo de 90º. O círculo trigonométrico serve para determinar funções trigonométricas.

2) O círculo trigonométrico é dividido em quatro quadrantes, cada um contendo um ângulo de 90º.

2ª Etapa: O círculo trigonométrico e o estudo das funções

Pergunta orientadora: Como o círculo trigonométrico pode ser usado para explicar as propriedades periódicas das funções seno e cosseno?

Leia o texto disponível em: Matemática.pt
Acesso em: 11 de julho de 2024

A partir da leitura do texto acima, responda às seguintes perguntas:

1) Qual é o valor do seno de um ângulo de 90º no círculo trigonométrico?

2) Qual é o valor do cosseno de um ângulo de 180º no círculo trigonométrico?

3) Qual é a relação entre graus e radianos no círculo trigonométrico?

4) O que representa o eixo horizontal no círculo trigonométrico? E o eixo vertical no círculo trigonométrico?

Gabarito:

1) O valor do seno de um ângulo de 90º no círculo trigonométrico é 1.

2) O valor do cosseno de um ângulo de 180º no círculo trigonométrico é -1

3) A relação é que 180º é igual a πpi radianos.

4) O eixo horizontal no círculo trigonométrico representa o valor do cosseno dos ângulos. O eixo vertical representa o valor do seno dos ângulos.

3ª Etapa: Cheque seus conhecimentos

Resolver questões é extremamente importante para fixar um assunto, notadamente quando estudamos matemática. Abaixo, seguem alguns exemplos de questões sobre o tema estudado:

Leia o texto disponível em: Toda Matéria
Acesso em: 11 de julho de 2024.

1)  Seja A o conjunto formado pelos seis primeiros múltiplos de , determine o seno de cada um dos arcos.

2)  (CESGRANRIO) Se  é um arco do 3º quadrante e  então  é:

3) Determine em qual quadrante está localizado o ângulo de 2735° no sentido positivo.

Gabarito:

1) Os seis primeiros múltiplos são, em graus:

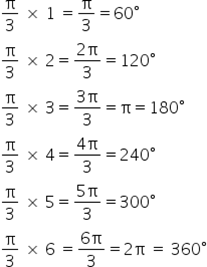
Para determinarmos os valores do seno, devemos fazer o estudo do sinal por quadrante:

1º quadrante (seno positivo)

2° quadrante (seno positivo)

3º quadrante (seno negativo)

4º quadrante (seno negativo)

2) Como tg x = 1, x deve ser um múltiplo de 45º que gere um valor positivo. Logo, no terceiro quadrante, este ângulo é 225º.

No primeiro quadrante, cos 45º = , no terceiro quadrante, cos 225º = .

3) Como cada volta completa possui 360°, dividimos 2 735 por 360.

São sete voltas completas mais 215º.

O ângulo de 215º está no terceiro quadrante no sentido positivo (anti-horário).

Questões e gabarito disponíveis em: Toda Matéria
Acesso em: 11 de julho de 2024.

Roteiro de estudos elaborado pela Professora Gabriela Ribeiro do Prado.

Coordenação Pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.

Revisão textual: Professora Daniela Leite Nunes.

Crédito da imagem: desifoto – Getty Images