Conteúdos
Este plano de aula de matemática apresenta o conceito de função modular. O material inicia discutindo o conceito de módulo, do ponto de vista geométrico. Logo em seguida, as principais propriedades para o módulo de um número real são apresentadas. Faz-se uma breve revisão a respeito da diversidade de tipos de funções, para, na etapa posterior, concentrar-se na função modular. Na penúltima etapa, são apresentados alguns exemplos de cálculo do valor numérico para a função modular. Finaliza-se com a construção do gráfico para um tipo específico de função modular, com o auxílio do aplicativo (gratuito) GeoGebra. O material também conta com algumas sugestões de textos e vídeos (em “Materiais relacionados”), para que o/a professor/a possa buscar aprofundamento sobre o assunto.
● Módulo de um número real;
● Propriedades do módulo de um número real;
● Tipos de funções;
● Função modular;
● Valor numérico de uma função modular; e
● Gráfico de uma função modular.
Objetivos
● Compreender o que é o módulo de um número real;
● Aprender as principais propriedades do módulo de um número real;
● Aprender a definição matemática de função modular;
● Aprender a calcular o valor numérico de uma função modular; e
● Familiarizar-se com gráficos de funções modulares.
Ensine também:
Situação problema envolvendo funções quadráticas (funções do 2º grau)
Inequação de 1º grau: significado e exercícios
Palavras-chave:
Módulo. Valor absoluto. Função modular.
Previsão para aplicação:
4 aulas (50 min./aula).
1ª Etapa: Módulo de um número real
Consideremos a reta numérica dos inteiros (Z):
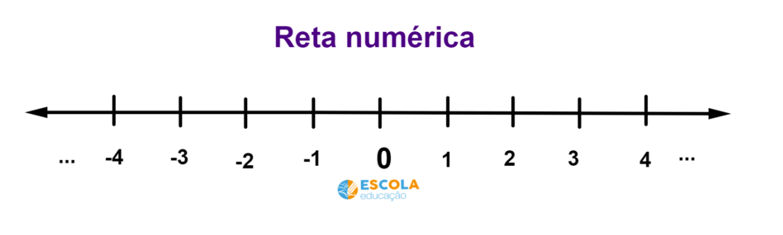
Suponhamos que se queira medir a distância do número 4 até a origem da reta, o número 0 (zero):
Se adotarmos a distância do número 0 (zero) até o número 1 como sendo uma unidade (1u), temos que a distância do número 4 até a origem da reta vale 4 unidades (4u).
Agora, suponhamos que se queira medir a distância do número −4 até a origem da reta:
Seria razoável adotarmos a distância do número 0 até o número −1 como sendo menos uma unidade (−1u), e, por consequência, obtemos como resposta que a distância do número −4 até a origem da reta vale menos quatro unidades (−4u)?
O conceito de distância negativa é algo bastante incômodo, para não dizer esdrúxulo.
É bem mais razoável considerarmos que, independentemente do sentido da reta dos inteiros, para a direita ou para a esquerda, a distância de um determinado número até a origem da reta (o número zero) é sempre positiva.
Dessa forma, tanto a distância do número 4 até a origem, quanto a distância do número −4 até a origem, valem quatro unidades (4u).
Pensando-se em situações como a que acabamos de analisar, criou-se um conceito em Matemática chamado de módulo, representado por dois traços verticais e paralelos (∣∣). Assim sendo, sempre que um número real estiver entre esses símbolos ∣∣ significa que estamos interessados no valor do seu módulo, também chamado de valor absoluto.
Geometricamente, o módulo de um número real pode ser encarado como a distância desse mesmo número até a origem da reta real . E, como já discutimos, a distância de um número até a origem da reta à qual ele pertence terá sempre um valor positivo. Logo, o módulo (ou valor absoluto) de um número real será sempre positivo .
De forma genérica, consideremos o número a. O seu módulo é representado da seguinte forma:
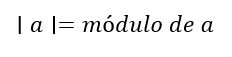
Para obtermos o módulo do número a devemos prosseguir da seguinte maneira:
![]()
Portanto, se o número a for positivo, ou nulo, o seu módulo será o próprio número a. Entretanto, se o número a for um número negativo, o seu módulo será o seu número simétrico .
Vejamos alguns exemplos de módulo de números reais:
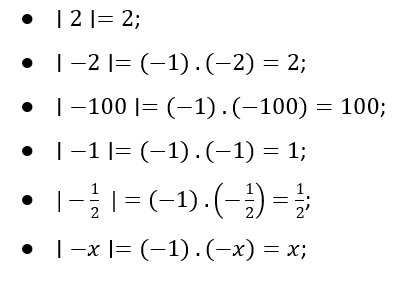
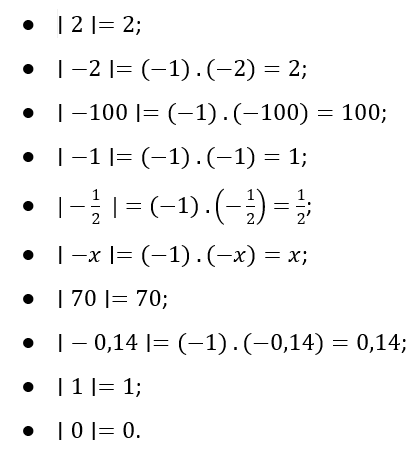
¹Começamos, por questões de simplicidade e didática, tratando da reta dos inteiros (Z). Contudo, o conceito de módulo pode ser aplicado para todos os números reais (R), representados pela reta real.
²Ou nulo.
³Também chamado de número oposto.
2ª Etapa: Propriedades do módulo de um número real
O módulo de um número real possui algumas propriedades importantes, a saber:
1ª propriedade: o módulo de um número real é igual ao módulo do seu número simétrico, ou seja:
![]()
2ª propriedade: o módulo de um número real ao quadrado é igual ao módulo ao quadrado desse mesmo número:
![]()
3ª propriedade: o módulo da soma de dois números reais (a e b) é menor ou igual à soma do módulo de cada um desses números:
![]()
4ª propriedade: o módulo da diferença entre dois números reais (a e b) é maior ou igual à diferença dos módulos de cada um desses números:
![]()
5ª propriedade: o módulo do produto de dois números reais (a e b) é igual ao produto dos módulos de cada um desses números:
![]()
6ª propriedade: o módulo da razão de dois números reais (a e b) é igual a razão do módulo de um número pelo módulo do outro número:
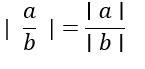
3ª Etapa: Tipos de Funções
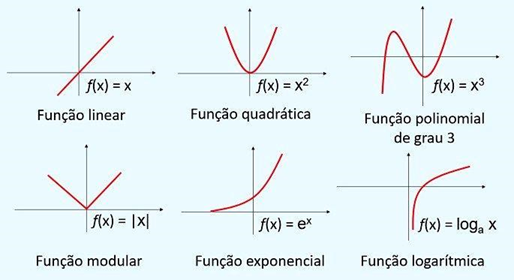
Existem diversos tipos de funções, dentre as quais podemos citar:
● Função do 1º grau, também conhecida como função afim. Esse tipo de função possui a seguinte lei de formação:

● E tantos outros tipos de funções…
Dentre esses outros tipos de funções, existe a função modular, que veremos a seguir.
4ª Etapa: Função modular
Para ser considerada uma função modular 4 , a função precisa ter, em sua lei de formação, ao menos uma variável dentro do módulo. Dessa forma, podemos ter vários tipos de funções modulares, pois, como vimos na etapa anterior, existem diversos tipos de funções: afim, linear, quadrática, logarítmica, exponencial etc. Qualquer um dos tipos de funções citadas podem se transformar em uma função modular, bastando, para isso, colocá-la dentro do módulo.
4 – A função modular possui domínio e contradomínio pertencentes ao conjunto dos números reais (R).
Vejamos alguns exemplos de funções modulares construídas a partir dos vários tipos de funções que foram apresentados na etapa anterior:

5ª Etapa: Valor numérico de uma função modular
Para encontrarmos o valor numérico de uma determinada função modular, basta substituir o valor (número) indicado para a incógnita na lei de formação da função em questão e, posteriormente, aplicar a definição matemática da função modular, vista na etapa anterior.
Vejamos alguns exemplos resolvidos:
Exemplo 1 – Considere a função modular f(x)=∣7x-2∣. Calcule o seu valor numérico para os seguintes casos:
a) x=5,
b) x=-3.
Resolução da letra a):
Primeiramente, substituímos o valor indicado para a incógnita na lei de formação da função modular:
f(5)=∣7.5-2∣ →
f(5)=∣35-2∣→
f(5)=∣33∣→
Como 33 é maior que zero (33>0), o seu módulo é ele mesmo:
f(5)=33
Resolução da letra b):
Novamente, iniciamos substituindo o valor indicado para a incógnita na lei de formação da função modular:
f(-3)=∣7.(-3)-2∣ →
f(-3)=∣-21-2∣→
f(-3)=∣-23∣→
Como -23 é menor que zero (-23<0), o seu módulo será o seu número simétrico:
f(-3)=(-1) .(-23)→
f(-3)=23
Exemplo 2 – Considere a função modular f(x)=∣x^2-12x + 4∣. Calcule o seu valor numérico para os seguintes casos:
a) x=2,
b) x=-5.


6ª Etapa: Gráfico de uma função modular
Acesso em: 17 de abril de 2022.
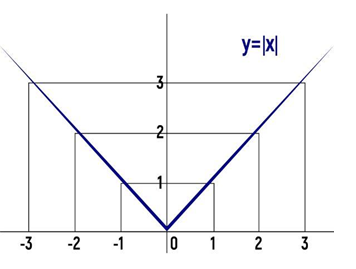
O gráfico de uma função modular exibe um comportamento bastante peculiar: o eixo das abscissas (x) se comporta como uma espécie de “espelho”, refletindo a parte do gráfico que teria as suas ordenadas (y=f(x)) com valores negativos.
Como já discutimos em etapas anteriores, o módulo de um número real é sempre positivo. Por consequência da definição matemática de função modular, ela admite apenas valores positivos para as suas ordenadas (y).
Para uma melhor visualização, trataremos do seguinte exemplo de função modular f(x)=y=∣x∣.
O gráfico da função f(x)=x (sem o módulo) é bastante conhecido. Substituindo alguns valores na função f(x)=x, obtemos os seguintes pares ordenados (pontos):
Tabela 1: f(x)=x

Utilizando o aplicativo GeoGebra, podemos construir o gráfico da função f(x)=x, e comparar os pontos obtidos (pares ordenados) na Tabela 1 com os pontos do gráfico gerado pelo aplicativo:
Gráfico 1: f(x)=x
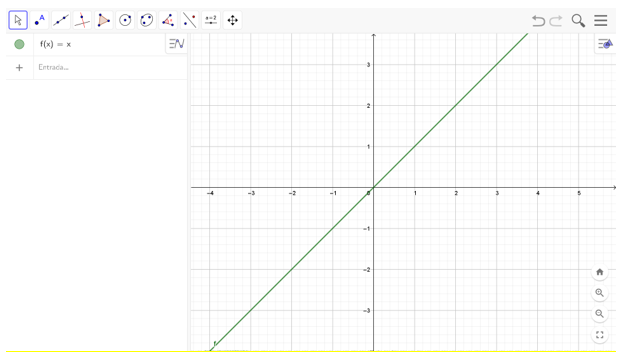
Conclui-se, assim, que o gráfico da função f(x)=x é uma reta na diagonal, inclinada para a direita, que passa pela origem do sistema de coordenadas (o ponto (0,0)).
Agora, vamos substituir os mesmos valores da Tabela 1 na função modular f(x)=y=∣x∣:
Tabela 2: f(x)=∣x∣

Mais uma vez, utilizaremos o aplicativo GeoGebra para encontrar o gráfico da função modular f(x)=y=∣x∣, e comparar os pares ordenados da Tabela 2 com os pontos do gráfico gerado pelo aplicativo:
Gráfico 2: f(x)=∣x∣
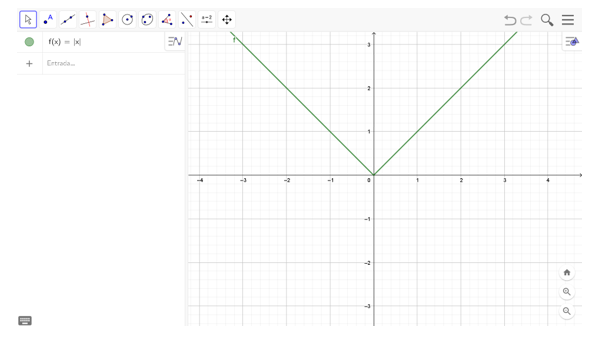
Dessa forma, tem-se que o gráfico da função modular f(x)=∣x∣ tem um formato semelhante à letra “V”, onde o eixo das abscissas (x) parece ter “refletido” a parte com valores negativos das ordenadas (y) do Gráfico 1: f(x)=x.
Plano de aula elaborado pelo Professor Elves Silva Moreira
Revisão textual: Professora Daniela Leite Nunes
Coordenadora Pedagógica: Prof.ª Dr.ª Aline Monge
Materiais Relacionados
● Para ler conteúdos sobre função modular:
Brasil Escola.
Acesso em: 24 de março de 2022.
Mundo Educação.
Acesso em: 24 de março de 2022.
Brasil escola.
Acesso em: 24 de março de 2022.
Infoescola.
Acesso em: 24 de março de 2022.
● Para ver vídeos sobre função modular:
Função Modular – Brasil Escola
Acesso em: 24 de março de 2022.
Função Modular: Conceitos Iniciais e Gráficos – Equaciona Com Paulo Pereira
Acesso em: 24 de março de 2022.