Conteúdos
Sequências;
Progressão Geométrica;
Soma infinita dos termos de uma PG;
Fractais;
Objetivos
Competência de área 1 – Construir significados para os números naturais, inteiros, racionais e reais.
H2 – Identificar padrões numéricos ou princípios de contagem.
H3 – Resolver situação-problema envolvendo conhecimentos numéricos.
H4 – Avaliar a razoabilidade de um resultado numérico na construção de argumentos sobre afirmações quantitativas.
Competência de área 2 – Utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela.
H8 – Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
Competência de área 5 – Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações algébricas.
H19 – Identificar representações algébricas que expressem a relação entre grandezas.
H21 – Resolver situação-problema cuja modelagem envolva conhecimentos algébricos.
H22 – Utilizar conhecimentos algébricos/geométricos como recurso para a construção de argumentação.
Caro professor, antes de dar sequência às atividades sugeridas neste plano de aula, consulte as abas "Material de Apoio" e "Para Organizar o seu Trabalho e Saber Mais".
1ª Etapa: Introdução do tema – triângulo de Sierpinski
O objetivo desse plano de aula é apresentar uma proposta para introduzir a soma infinita dos termos de uma PG.
Antes de introduzir a atividade, os alunos já devem conhecer as principais características das progressões aritméticas e geométricas. Acesse os links 3 e 7 para ver a sistematização da PA e PG. (links disponíveis na aba "Para Organizar o seu Trabalho e Saber Mais").
Inicie a aula explicitando algumas características dos fractais. Leve imagens para a sala e mostre alguns fractais. Você pode utilizar o link 2.
Nesse início, os alunos devem ter contato com as propriedades de auto-semelhança e a complexidade infinita dos fractais. Não entraremos em detalhes sobre a dimensão dos fractais.
Em seguida, divida os alunos em duplas ou trios. Cada grupo precisará de:
• Régua.
• Compasso
• Folha sulfite
• Lápis e borracha.
Entregue uma folha aos alunos com as seguintes instruções:
Triângulo de Sierpinski
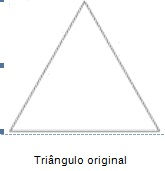
Neste trabalho vocês irão construir os quatro primeiros estágios do triângulo de Sierpinski e responder a um questionário no final.
TRIÂNGULO ORIGINAL
1º passo: Construa um triângulo equilátero com 16 cm de lado com auxílio da régua e compasso.
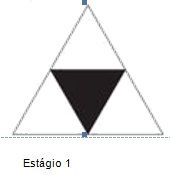
ESTÁGIO 1:
1º passo: Construa um triângulo equilátero com 16 cm de lado com auxílio da régua e compasso.
2º passo: Divida cada lado do triângulo em duas partes iguais (ou seja, encontre o ponto médio).
3º passo: Trace o triângulo no centro e ilustre-o da maneira que preferir.
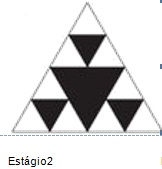
ESTÁGIO 2:
1º passo: Repita o estágio um.
2º passo: Divida cada lado dos novos triângulos brancos em duas partes iguais (ou seja, encontre o ponto médio).
3º passo: Trace o triângulo no centro de cada triângulo branco e ilustre-os da maneira que preferir.
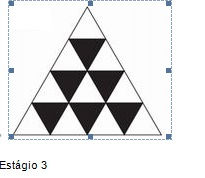
ESTÁGIO 3:
1º passo: Repita o estágio dois.
2º passo: Divida cada lado dos novos triângulos brancos em duas partes iguais (ou seja, encontre o ponto médio).
3º passo: Trace o triângulo no centro de cada triângulo branco e ilustre-os da maneira que preferir.
ESTÁGIO 4:
1º passo: Repita o estágio três.
2º passo: Divida cada lado dos novos triângulos brancos em duas partes iguais (ou seja, encontre o ponto médio).
3º passo: Trace o triângulo no centro de cada triângulo branco e ilustre-os da maneira que preferir.
QUESTÕES:
1. Escreva os cinco primeiros termos da sequência onde o 1º termo indica a quantidade de triângulos brancos no estágio original, o 2º termo indica a quantidade de triângulos brancos no estágio 1, e assim sucessivamente.
Resp: 1, 3, 9, 81, 243
2. Qual é o próximo termo desta sequência?
Resp: 729
3. O que acontece a cada novo termo?
Resp: Espera-se que o aluno perceba que a cada novo termo, o número de triângulos brancos triplica.
4. Se continuarmos o processo, quantos triângulos brancos teremos no estágio 10?
Resp: 19683 triângulos brancos.
5. Agora, vamos analisar o número total de triângulos em cada estágio. Escreva os cinco primeiros termos da sequência onde o 1º termo indica a quantidade de triângulos no estágio original, o 2º termo indica a quantidade de triângulos brancos no estágio 1, e assim sucessivamente.
Resp: 1, 4, 13, 94, 337.
6. Qual é o próximo termo desta sequência?
Resp: 337 + 729 = 1066.
7. O que acontece a cada novo termo?
Resp: Espera-se que o aluno perceba que o n-ésimo termo dessa sequencia é igual à soma dos n primeiros termos da sequência construída na questão 1.
8. Quantos triângulos teremos se continuarmos o processo indefinidamente?
Resp: Termos um número infinito de triângulos.
Observe que foi pedido ao aluno que, a cada etapa da construção do triângulo de Sierpinski, pintasse o triângulo do centro. De fato, o triangulo central deve ser removido, mas optamos pela ilustração para facilitar o manuseio dos materiais e a aplicação da atividade.
2ª Etapa: Situação-Problema
Depois que os grupos terminarem de registrar as respostas comente que, se continuarmos o da construção do triângulo de Sierpinski indefinidamente, teremos infinitos triângulos. Em seguida, proponha a seguinte questão: Já que o número de triângulos é infinito, podemos dizer que a área pintada também será infinita?
O objetivo é gerar um conflito. Em geral, os alunos se espantam coma a ideia de que a soma da área de infinitos triângulos não é um número infinito. Você pode conduzir a discussão da seguinte forma:
1. Construa a tabela com os valores da medida do lado do triângulo branco (cm) e a área de cada triângulo branco (cm2) em cada estágio.
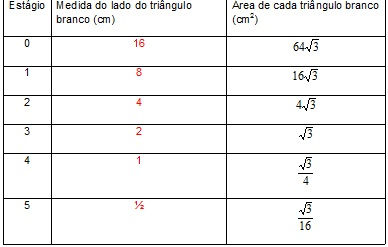
2. Pergunte o que ocorre com a medida do lado do triângulo branco a cada novo termo. Espera-se que os alunos percebam que a cada novo termo a medida do lado do triângulo branco se reduz à metade.
3. Pergunte o que ocorre com a área do triângulo branco a cada novo termo. Espera-se que os alunos percebam que a cada novo termo a área do triângulo branco se reduz à quarta parte.
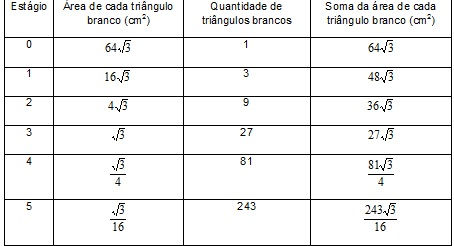
4. Peça aos alunos que calculem á área dos triângulos brancos nos seis primeiros estágios. Basta multiplicar a área do triângulo branco pela quantidade de triângulos brancos em cada estágio.
5. Pergunte o que ocorre com a soma da área dos triângulos brancos a cada novo termo. Espera-se que os alunos percebam que a cada novo termo a área do triângulo branco é multiplicada por ¾.
6. Peça aos alunos que calculem a área pintada do triângulo nos seis primeiros estágios. Basta subtrair a soma da área dos triângulos brancos da área do triângulo inicial.
7. Conclua, com os alunos, que a cada novo termo a área se aproxima à área do triângulo inicial, ou seja, a área tende a ![]() . Esse valor é resultado de
. Esse valor é resultado de ![]() .
.
3ª Etapa: Sistematização dos conteúdos abordados
Sistematize a soma infinita de termos de uma PG. A formalização da fórmula pode ser feita a partir de sua demonstração. Acesse o link 3 para ver a demonstração.
Em seguida, relacione a atividade anterior à fórmula e proponha novas questões.
Materiais Relacionados
Caro professor, para esta atividade é importante que se aproprie de algumas informações sobre o tema. Selecionamos os links abaixo para ajudá-lo.
• Material sobre fractais
– Link 1
– Link 2 (veja a área Galeria de Fractais)
• Material sobre progressão geométrica.
Link 3
• Experimento intitulado “O quadrado de Koch”
– Link 4 (experimento)
– Link 5 (guia do professor)
• Material sobre progressão aritmética:
– Link 6
– Link 7
• Vídeo sobre o triângulo de Sierpinski, Episódio 6 – Tema: Fractais – Título: Um Triângulo Fractal Especial.
– Link 8
• Livro:
– CARVALHO, Maria Cecília Costa e Silva. Padrões numéricos e sequências. São Paulo: Moderna, 1997.

