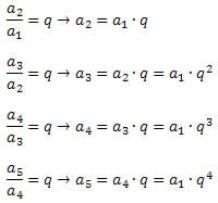Conteúdos
• Progressão geométrica;
• Soma de PG finita e infinita de uma PG de razão entre -1 e 1;
• Noção de limite;
Objetivos
• Observar padrões em sequências figurativas.
• Compreender o paradoxo de Zenão.
• Compreender e reproduzir a demonstração da fórmula da soma de uma PG finita.
• Compreender a noção de limite e aplicar à soma de termos de uma PG infinita.
1ª Etapa: Soma de uma PG infinita
A quarta questão deve instigar os alunos a imaginar que precisaríamos de uma figura de ordem infinita para alcançar o valor. Não dê a resposta aos alunos, antes disso, apresente o vídeo “À espera da meia-noite” da série Matemática na Escola – Unicamp. O vídeo traz informações sobre o problema clássico do paradoxo de Zenão e introduz o conceito de limite de sequências.
Após o vídeo, peça para os alunos calcularem Sn para a PG de a1 = 0,25A e q = 3?0,25 = 0,75
Mas 0,75∞ = 0, observe o gráfico da função f(x) = 0,75x:
Quanto maior o valor de x, mais próximo de zero é a função. Quando x tende ao infinito, então o resultado da potência tende a zero.
Podemos generalizar a fórmula para casos em que a razão da PG é tal que -1 < q < 1:
2ª Etapa: início de conversa – uma questão do Enem
Inicie a aula apresentando a questão proposta no Enem em 2008:
Fractal (do latim fractus, fração, quebrado) — objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial.
A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais — objetos geométricos formados por repetições de padrões similares.
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. comece com um triângulo equilátero (figura 1);
2. construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2;
4. repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
Esta é uma questão simples, exige apenas que o aluno observe um padrão figurativo e determine a figura seguinte da sequência.
Porém, podemos explorar um pouco mais.
Peça aos alunos para que analisem a área em branco de cada figura.
A primeira está completamente pintada, ou seja, a área branca é igual a zero.
A segunda figura tem 25% de área em branco, ou seja, 0,25A. Note que o triângulo inicial foi dividido em 4 partes e uma delas é branca.
A terceira figura é composta por dois tamanhos de triângulos brancos; o maior tem área 0,25A e os três triângulos menores têm área 0,252A. Logo, a área branca da terceira figura é igual a 0,25A + 3 ? 0,252A.
A quarta figura tem, além dos triângulos brancos da figura 3, outros 9 triângulos de área 0,253A. . Logo, a área branca da quarta figura é igual a 0,25A + 3 ? 0,252ª + 9 ? 0,253A.
Organizando as informações, podemos determinar a área de uma figura n qualquer.
Note que a área de cada figura é resultado de uma somatória de termos de uma PG:
A PG formada é crescente de primeiro termo igual a 0,25A e razão 3 ? 0,25.
Deste modo, para encontrar a área branca da n-ésima figura, devemos encontrar a soma dos n1 termos dessa PG.
3ª Etapa: Soma de uma PG finita
Junto com os alunos, deduza a fórmula de acordo com os passos que seguem:
1. A soma dos termos de uma P. G. é dada por:
Sn = a1 + a2 + a3 + … + an
Logo, se multiplicarmos esta soma pela razão da P. G. ficamos com
q?Sn = q?a1 + q?a2 + q?a3 + … + q?an
2. Agora, lembrando que também podemos obter o n-ésimo termo por an = a(n-1)?q, temos
q?Sn = q?a1 + q?a2 + q?a3 + … + q?an =
a2 + a3 + a4 + … + an + a(n-1)
3. Assim, se subtrairmos Sn e q?Sn, obteremos:
(1 – q)Sn = a1 – a(n-1)
(1 – q)Sn = a1 – a1?qn
(1 – q)Sn = a1 (1 – qn)
Assegure-se de que todos compreenderam os passos realizados.
4ª Etapa: Voltando ao contexto da questão do Enem
Fale aos alunos que precisarmos fazer um pequeno ajuste com o índice da somatória para o contexto da questão do Enem. Observe a tabela:
Logo, para o contexto da questão do Enem, temos que encontrar a Soma dos (n-1) primeiros termos da PG de primeiro termo 0,25A e razão 3 ? 0,25.
Proponha algumas perguntas para que os alunos utilizem a fórmula da soma da PG:
1) Qual á área branca da décima figura?
2) Qual a área branca da vigésima figura?
3) Explique o que ocorre com a área branca da figura conforme aumentamos a ordem da figura.
4) Suponha que a área preta da figura inicial é igual a 10 cm2. Qual a ordem da figura que terá área branca igual a 10 cm2?
Materiais Relacionados
1. O vídeo “À espera da meia-noite”, apresenta o problema clássico do paradoxo Zenão relacionando com uma situação do dia a dia.
2.
O experimento
“O quadrado de Koch”, oferece uma proposta interessante que relaciona a PG a alguns aspectos de um fractal. Ela pode ser utilizada para introduzir a soma infinita de uma progressão aritmética.
Arquivos anexados
- Soma de uma PG de razão entre -1 e 1