Conteúdos
Este plano de aula de Matemática apresenta, de forma introdutória, o conceito de duas entidades matemáticas fundamentais: o ponto e a reta. Posteriormente, a partir desses conceitos, apresenta-se a ideia de semirreta e, logo em seguida, de segmento de reta. Ao final, aborda-se os principais tipos de segmentos de reta. O material conta, ainda, com algumas sugestões de textos e vídeos, para que o/a professor/a possa buscar um maior aprofundamento sobre o assunto.
- Introdução;
- Semirreta;
- Segmento de reta; e
- Tipos de segmento de reta.
Objetivos
- Compreender o que é uma reta e como ela é formada;
- Compreender o que é uma semirreta e como ela é formada;
- Compreender o que um segmento de reta e como ele é formado; e
- Aprender quais são os principais tipos de segmento de reta que existem.
1ª Etapa: Introdução
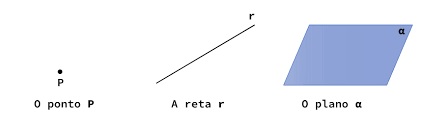
Ao estudarmos Matemática, a compreensão de alguns objetos (entes) matemáticos fundamentais (tais como: o ponto, a reta e o plano), mostra-se imprescindível. O entendimento adequado de tais objetos matemáticos nos possibilitam fazer estudos sistemáticos em diversas áreas da Matemática, como na Geometria Plana, na Geometria Espacial e na Geometria Analítica.
Neste plano de aula, vamos nos concentrar nos primeiros dois objetos matemáticos citados: o ponto e a reta, para depois tratarmos de entes matemáticos, como a semirreta e o segmento de reta.
O ponto é um objeto (ente) matemático adimensional, ou seja, ele não possui nenhuma dimensão espacial. Provavelmente devido a essa característica, o ponto é um dos (se não o mais) objetos matemáticos mais abstratos que existem no arcabouço de conhecimentos da Matemática.
Usualmente, quando queremos representar um determinado ponto, utilizamos letras latinas maiúsculas (A, B, C, D, E, F…).
Uma reta é um objeto (ente) matemático unidimensional (possui uma única dimensão espacial) formado por infinitos pontos (alinhados). É interessante notar que um conjunto infinito de objetos matemáticos adimensionais, os pontos, são os elementos que servem de base para a construção de um objeto matemático que possui uma dimensão espacial: a reta.[1]
As retas são entes matemáticos infinitos nos seus dois sentidos[2]. Usualmente, utilizamos letras latinas minúsculas para representá-las (r, s, t, u, v…). Além de sentido (direita e esquerda), uma reta possui direção, tais como: vertical, horizontal e inclinada[3]. Vejamos a seguir a representação da reta s:

[1] Tal constatação pode servir de gatilho para diversas discussões, inclusive de caráter filosófico. No entanto, conduzir ou não a aula por esse caminho, fica a critério do(a) professor(a).
[2] Para indicar essa infinitude, utilizamos setas nos dois sentidos da reta, indicando que ela continua infinitamente nos dois sentidos. A reta é um objeto matemático infinito e ilimitado.
[3] A diagonal é um caso específico de uma direção inclinada.
2ª Etapa: Semirreta
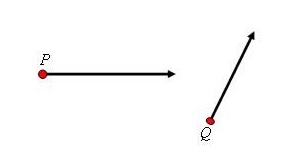
Como já foi dito anteriormente, uma reta é um ente matemático infinito[1] nos seus dois sentidos. Assim, a semirreta pode ser identificada como um “pedaço” da reta. Ou seja, uma semirreta possui uma origem (um início) e um único sentido, no qual ela cresce infinitamente.
Uma semirreta também é constituída por infinitos pontos, posto que ela é infinita em um dado sentido.
Com a utilização de dois pontos pertencentes a uma mesma semirreta, podemos representá-la como:
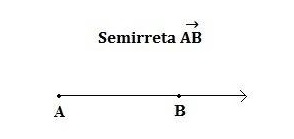
O ponto A representa a origem da semirreta, que passa pelo ponto B, e segue infinitamente no sentido indicado pela seta na figura. Para representarmos uma semirreta, escrevemos primeiro o ponto que indica a sua origem, e em seguida escrevemos um segundo ponto, pertencente à mesma semirreta, com uma seta sobre os dois pontos. Para o caso da semirreta da figura anterior, escrevemos: .
[1] A reta é um ente matemático infinito e ilimitado.
3ª Etapa: Segmento de reta

Como vimos, a reta é um ente matemático unidimensional, infinito nos seus dois sentidos. Uma semirreta (que também é unidimensional), no entanto, possui uma origem, um início, e é infinita em um único sentido.
Diferentemente da reta e da semirreta, um segmento de reta não é infinito em nenhum sentido, ou seja, ele possui um ponto inicial (uma origem) e um ponto final, os quais também podem ser chamados de extremos do segmento de reta.
Na figura desta seção, temos a reta r, que é, naturalmente, infinita nos dois sentidos. Como sabemos, uma reta é composta por infinitos pontos. Assim sendo, podemos escolher dois desses pontos para servirem de extremos de um determinado segmento de reta que, no caso da figura em questão, está sendo representado pelo pedaço vermelho da reta r.
Podemos identificar um segmento de reta por meio dos seus dois pontos (extremos) indicados por duas letras latinas maiúsculas (pontos), com um traço sobre as duas letras. Para o caso da figura desta seção, representamos o segmento de reta da seguinte forma: ; ou .
Desta forma, temos que um segmento de reta é um ente matemático finito, ou seja, possui início e fim.
4ª Etapa: Tipos de segmento de reta
Dependendo da forma como os segmentos de reta estão dispostos (ou seja, de acordo com as suas posições) em um determinado plano, eles são classificados como:
1) Segmentos consecutivos: quando possuem um ponto em comum.

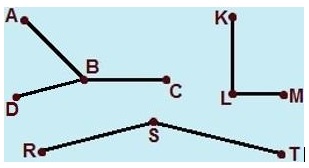
Os segmentos de reta , e possuem o ponto B em comum, logo, são consecutivos.
De forma análoga, os segmentos de reta e possuem o ponto L em comum e, por isso, também são segmentos de reta consecutivos.
Por último, os segmentos de reta e possuem o ponto S em comum, portanto também são segmentos de reta consecutivos.
2) Segmentos colineares: quando dois ou mais pontos dos segmentos de reta pertencem à mesma reta.
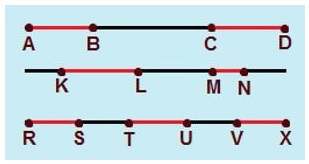
Percebemos que os segmentos de reta e pertencem à mesma reta, o que significa que a mesma reta passa por esses dois segmentos de reta.
Notamos também que os segmentos de reta e exibem o mesmo comportamento. Logo, são segmentos de reta colineares.
Os segmentos de reta , e também pertencem à mesma reta, ou seja, a mesma reta passa por esses três segmentos de reta.
3) Segmentos adjacentes: quando dois segmentos de reta são, simultaneamente, consecutivos e colineares.
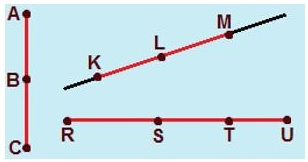
4) Segmentos congruentes: quando dois (ou mais) segmentos de reta possuem exatamente a mesma medida, o mesmo tamanho, o mesmo comprimento.

Materiais Relacionados
- Para ver conteúdos sobre segmento de reta:
https://brasilescola.uol.com.br/matematica/segmentos-retas.htm.
Acesso em: 29 de novembro de 2021.
https://www.todamateria.com.br/segmento-de-reta/.
Acesso em: 29 de novembro de 2021.
https://matematicabasica.net/segmento-de-reta/
Acesso em: 29 de novembro de 2021.
https://www.infoescola.com/matematica/segmento-de-reta/
Acesso em: 29 de novembro de 2021.
- Para ver vídeos sobre segmento de Reta:
Reta, Semirreta e Segmento de Reta – Gis com Giz Matemática
Acesso em: 29 de novembro de 2021.
Reta, semirreta e segmento de reta – Matemática no Papel
Acesso em: 29 de novembro de 2021.
Diferença entre: Reta, Semirreta e Segmento de Reta – Professora Angela Matemática
Acesso em: 29 de novembro de 2021.

