Conteúdos
Sistema de equações do 1º grau.
Objetivos
Discuta sobre as possíveis soluções de um sistema com 2 equações do 1º grau com duas incógnitas.
Apresente um procedimento de resolução de sistema de equações do 1º grau por meio de gráficos.
1ª Etapa: Aprofundando a discussão
Nem todo sistema de equações do 1º grau possuem uma solução única, em alguns casos há uma infinidade de soluções, em outros não há solução alguma. A representação das equações no plano cartesiano pode contribuir muito para que o aluno compreenda esta diferença.
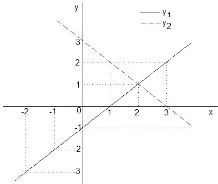
Proponha aos alunos que encontre a solução dos sistemas abaixo, representando graficamente as retas no GeoGebra.
Na resolução do primeiro sistema, temos duas retas que passam pelos mesmos pontos, ou seja, há uma infinidade de valores que fazem parte da solução: S = {(1, 2), (-1, 3), (5, 0), …} (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Porém, no segundo sistema, temos duas retas que não tem ponto algum em comum. Observe no gráfico que as duas retas são paralela. Desse modo, S = { }. (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
2ª Etapa: Aplicando os conhecimentos construídos
Disponibilize aos alunos uma lista com situações-problema envolvendo sistemas de equações do 1º grau. Você pode pedir que resolvam em trios para que troquem informações e discutam sobre as formas de resolução.
3ª Etapa: Início de conversa – O problema da lanchonete
Proponha o seguinte problema para a sala:
4ª Etapa: A resolução a partir do gráfico – utilizando o Geogebra
Explique aos alunos que as duas equações formam um sistema de equações do 1º grau, e que elas podem ser resolvidas graficamente. O problema anterior gera o seguinte sistema:
Cada uma das equações pode ser representada no plano cartesiano, e a solução dele será dada pelo ponto que pertencer às duas equações. Note que, no gráfico abaixo, K = C. (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Leve os alunos ao labortório de informática e mostre como utilizar o software Geogebra. Sugerimos que resolva um sistema junto com os alunos. Veja o exemplo a seguir. (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Primeiro vamos encontrar dois pontos que satisfazem a equação 3x + 2y = 58. Atribuindo um valor a x, encontramos o valor de y: (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Vamos chamar identificar ponto por A e B: A = (0, 29) e B = (2, 26). Em seguida, digitamos cada ponto na “entrada” do Geogebra: (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Depois, selecione o botão “Reta” no menu e clique nos dois pontos por onde a reta deve passar. (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Para encontrao o ponto que as duas retas tem em comum, clique no botão “Ponto” no menu e selecione a opção “intersecção de dois objetos”. (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
Sobre a intersecção das duas retas deve aparecer um quinto ponto, o qual é solução do sistema: (Veja a tabela/ figura/ imagem no material de apoio anexo nesse plano de aula)
5ª Etapa: vídeo “A voz do interior”
Apresente o vídeo “A Voz do interior”, aos alunos. Assim que o problema dos porcos e galinhas for apresentado, pause a reprodução do vídeo. Peça aos alunos que tentem resolver o problema e verifique as estratégias utilizadas. Em geral, os alunos mostram maior dificuldade em transformar as informações do problema em sentenças matemáticas. Verifique se compreenderam os dados do problema e se foram capazes de registrar matematicamente as informações utilizando expressões algébricas.
Materiais Relacionados
1. O GeoGebra é um software de matemática dinâmica gratuito e multi-plataforma para todos os níveis de ensino, que combina geometria, álgebra, tabelas, gráficos, estatística e cálculo em um único sistema. Abaixe o programa e conheça dicas e sugestões no site.