Conteúdos
• Teorema de Pitágoras: história, demonstração e aplicações.
Objetivos
• Discutir sobre a história da matemática e sobre as contribuições de Pitágoras, considerando, principalmente a sua contribuição para a argumentação e dedução lógica matemática.
• Apresentar a demonstração do Teorema de Pitágoras.
• Propor situações-problema envolvendo o Teorema de Pitágoras.
• Formular situações-problema para propor aos colegas de sala.
1ª Etapa: Início de conversa
A História da Matemática pode aguçar a curiosidade dos alunos por temas matemáticos. Porém, dizer que Pitágoras nasceu em 565 a.C. na ilha grega de Samos, leste do mar Egeu, e que era uma pessoa brilhante pode não instigar seus alunos suficientemente. Mas o que você acha de contar que, além da Escola Pitagórica, o famoso grego fundou uma religião que, segundo Paul Strathern (1998):
[…] Continha uma longa lista de mandamentos birutas que seus discípulos deviam seguir. Não lhes era permitido pegar nada que caísse ou passar por cima de uma vara, nem colher flores ou pôr as mãos em um frango branco. Também era absolutamente proibido comer feijão, o que Pitágoras explicava dizendo que o grão de feijão, colocado em uma sepultura recente e coberto com esterco por quarenta dias, adquire forma humana.
(Paul Strathern, 1998, p. 9-10)
Proponha aos alunos que leiam o livro sugerido no link 1. Se não dispuser do livro, substitua por outros textos sobre ele, como o sugerido no link 5. Após a leitura, converse com o grupo, questionando-os sobre o que mais agradou sobre a história de Pitágoras. É provável que as curiosidades que o fazem ser interpretado como um “louco” sejam as mais mencionadas. Mas explique que uma das maiores contribuições dele foi o conceito de prova em matemática.
2ª Etapa: Tangram pitagórico com quadrados
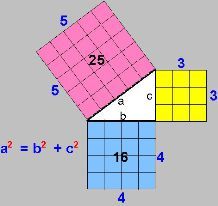
Leve os alunos para a sala de informática e proponha que resolvam o quebra-cabeça sugerido no link 3. Neste quebra-cabeça, o aluno deve construir um quadrado sobre cada lado do triângulo retângulo com as peças verdes e amarelas.
Em seguida, pergunte aos alunos o que eles observam em relação aos quadrados formados sobre cada lado do triângulo. Conduza a discussão até que identifiquem que a área sobre o lado maior do quadrado (a hipotenusa) é igual à soma das áreas dos outros dois quadrados sobre os outros lados (os catetos).
Escreva o teorema de Pitágoras na lousa, definindo os nomes dos lados do triângulo retângulo. Proponha um problema em que os alunos conheçam o valor dos catetos e precisem calcular o valor da hipotenusa.
3ª Etapa: Demonstração do Teorema de Pitágoras
Há diversas demonstrações do Teorema de Pitágoras, por isso, se houver tempo suficiente, organize os alunos em grupos, peça que pesquisem uma demonstração do teorema apresentem aos colegas.
Oura forma de apresentar a demonstração do teorema, é oferecer aos alunos uma folha com a demonstração. (Veja a demonstração clássica do teorema nas páginas 7 e 8 da monografia de Juliane Amaral de Oliveira, sugerido no link 2)
Peça aos alunos que sentem-se em duplas e que leiam a demonstração. Passe entre as duplas para ouvir o que conversam e verificar se todos entendem a linguagem. É previsível que surgirão muitas dúvidas. Em seguida, converse com a sala sobre cada etapa da demonstração, garantindo que todos a tenham compreendido.
4ª Etapa: Aplicando o Teorema de Pitágoras
Disponibilize aos alunos uma lista com situações-problema envolvendo a aplicação do Teorema de Pitágoras. Você pode pedir que resolvam em trios para que troquem informações e discutam sobre as formas de resolução.
Em seguida, solicite aos alunos que criem individualmente uma situação-problema. Cada trio deve reunir as três questões em uma folha. Recolha o material e redistribua aleatoriamente entre os grupos. Eles deverão resolvê-las e, ao término, compartilhar com a sala os resultados obtidos.
Materiais Relacionados
1. Para saber mais sobre a vida de Pitágoras, leia o livro intitulado “Pitágoras e seu teorema” da Editora Jorge Zahar, escrito por Paul Strathern. (Coleção Cientistas em 90 minutos)
2. Monografia de Juliane Amaral de Oliveira intitulada “Teorema de Pitágoras” e disponível em: http://www.mat.ufmg.br/~espec/monografiasPdf/Monografia_Juliane.pdf.
3. Jogo eletrônico Descobrindo o Teorema de Pitágoras, com o Tangram Pitagórico com Quadrados disponível em: http://www.uff.br/cdme/tangrans_pitagoricos_eletronico/index.html.
4. Vídeo disponível em https://www.youtube.com/watch?v=1er3cHAWwIM. O vídeo ilustra o Teorema de Pitágoras. Note, porém, que ele não serve para demonstrar o Teorema, pois sobre cada lado do triângulo foi construído um prisma de base quadrangular, e todos possuem a mesma altura.
5. Saiba mais sobre a história de Pitágoras em http://chc.cienciahoje.uol.com.br/o-teorema-de-pitagoras/ e http://chc.cienciahoje.uol.com.br/a-irmandade-pitagorica/
6. Veja uma situação problema com o teorema de Pitágoras em http://www.obm.org.br/export/sites/default/semana_olimpica/docs/2012/Pitagoras.ppt
Arquivos anexados
- Quem é esse tal de Pitágoras?