Conteúdos
– Educação financeira
– Proporção
– Razão
Objetivos
– Adquirir maior capacidade crítica ao consumir
– Ampliar o vocabulário relacionado à proporcionalidade
– Resolver problemas de proporcionalidade com base em relações numéricas e cálculo mental ou escrito
1ª Etapa: Início de conversa
Administrar o dinheiro é um tarefa presente na vida cotidiana. Esta atividade pode envolver um conjunto grande e complexo de aplicações da matemática. No contexto do ensino fundamental II, noções de razão e proporção são úteis para formar um consumidor mais crítico e consciente.
A oferta de um mesmo produto em embalagens contendo diferentes quantidades é presente em diversos momentos da vida corriqueira. No entanto, decidir qual destas embalagens contém o produto realmente mais barato pode ser uma tarefa desafiadora. Um bom exemplo são os pacotes do mesmo alimento costumeiramente vendidos em diversos tamanhos. Como decidir entre dois pacotes de 500 g ou um pacote de 1 kg?
Ao final desta aula, o estudante será capaz de tomar este tipo de decisão de forma consciente utilizando de noções de razão e proporção.
2ª Etapa: Motivação dos estudantes e diagnóstico do conhecimento prévio
Nessa etapa, o professor deve motivar os estudantes a pensar rapidamente no tipo de situação que será levantada durante a aula, além de diagnosticar o conhecimento prévio. O educador conduzirá uma aula expositiva de forma dialogada mobilizando o raciocínio dos estudantes e propondo problemas. Estes problemas podem ser trabalhados em duplas com a supervisão do responsável.
Proponha o seguinte problema:

Solução:
Organize as informações do enunciado em uma tabela como esta:
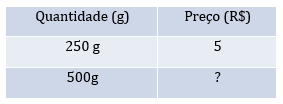
Note que de 250 para 500, o preço foi multiplicado por 2 (aqui vale a pena estimular o cálculo mental). Como o enunciado pede que o aumento seja proporcional, então o preço deve também ser multiplicado por 2.
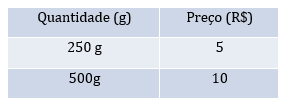
Concluímos que, se o aumento for proporcional, a lata com 500 g custaria R$ 10,00.
De forma a diagnosticar o conhecimento prévio dos estudantes, o seguinte exercício contém espaço para maior elaboração teórica e discussão das estratégias fundamentais necessárias para trabalhar com razões e proporções.

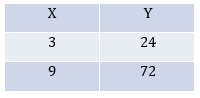
Solução:
Este é o momento de relembrar os estudantes das relações de proporcionalidade numa tabela deste tipo. Aproveite para diagnosticar o quanto o grupo conhece do assunto aqui.
Note que:
9 é o triplo de 3
72 também é o triplo de 24 (por quê?)
24 é igual a 3×8 e 72 é igual a 9×8 (por quê?)
A resposta destes “porquês” é a mesma: porque tratam-se de grandezas diretamente proporcionais.
Neste momento, o professor pode levantar um diálogo com os estudantes sobre quais grandezas o grupo conhece que, quando uma cresce (ou diminui) a outra cresce (ou diminui) também.
3ª Etapa: Aprendendo a economizar
Dada a motivação e relembrados alguns conceitos de proporcionalidade direta, o professor deve relacionar este conhecimento prévio com situações problema.
O educador pode iniciar levantando a seguinte questão para o diálogo com o grupo:

A resposta é não.
O professor pode exibir um exemplo real. Sugere-se acessar o site de alguma grande rede de supermercados e realizar uma rápida pesquisa para elaborar o próximo problema com dados reais e atualizados. Uma opção é o site da rede “Pão de Açúcar”. Na busca, há a opção de filtros e é fácil localizar o mesmo produto, da mesma fabricante e com quantidades distintas. Caso o acesso não seja possível, a seguir, há um exemplo retirado desta mesma página com algumas pequenas adaptações por motivos didáticos.

Solução:
Organize as informações do enunciado em uma tabela como esta:
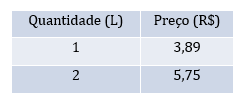
Com um cálculo rápido, é possível observar que essas grandezas não são diretamente proporcionais. Note que se comprássemos duas embalagens de um litro pagaríamos R$ 7,78, enquanto que se comprássemos uma embalagem de dois litros pagaríamos R$ 5,75.
Partiremos para o último problema. Agora com um grau um pouco maior de complexidade.
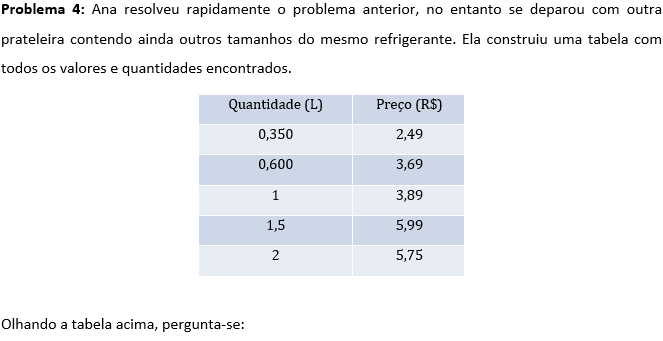

Solução:
a) Primeiro, vamos analisar quanto custaria comprar 2 litros em cada caso.
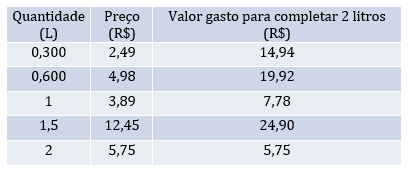
b) Vale observar com os estudantes que algumas opções nos obrigam a comprar mais do que dois litros. Então deve-se escolher aquelas que se aproximam mais de dois litros possível. Observa-se que a garrafa com dois litros permanece sendo a mais barata.
c) Note que as embalagens de 0,3 l , 0,6 l e 1,5 l têm valores proporcionais. Aqui vale uma observação importante ao professor: o que se paga por produto é proporcional nesses casos. Isso significa que o preço por litro não muda. Diferente dos outros casos.
4ª Etapa: Preparação para a ação
Após o contato dos estudantes com os tópicos apresentados, vale propor uma atividade prática para que eles se apropriem do conhecimento adquirido. O objetivo dessa atividade é oportunizar a aplicação do conhecimento prévio sobre a razão, a proporção e a capacidade crítica no momento do consumo por meio da simulação de compras num supermercado construído pelos próprios estudantes.
O material necessário para esta atividade será:
– Impressão de algumas planificações encontradas aqui (veja as instruções abaixo para saber quais e quantas imprimir)
– Etiquetas adesivas
– Cola, tesoura e lápis de cor
O professor escolherá cinco (ou mais) produtos comumente encontrados no mercado para que os estudantes confeccionem as embalagens partindo das planificações de figuras geométricas. Os produtos podem ser, por exemplo: molho de tomate, sabão em pó, caixa de cereais, bolachas e suco natural. O educador deve imprimir as planificações, para que os estudantes possam confeccionar as embalagens.
Para cada produto escolhido, o professor deve decidir ao menos três versões de quantidades distintas com preços proporcionais e não proporcionais. No caso do molho de tomate, por exemplo:
– 250 g de molho de tomate por R$ 5,00
– 500 g de molho de tomate por R$ 7,00
– 1 kg de molho de tomate por R$ 15,00
Por último, o professor deve decidir uma lista de compras contendo os itens disponíveis. Uma possível lista seria:
– 1 kg de molho de tomate
– 500 g de sabão em pó
– 300 g de cereais
– 50 g de bolachas
– 3 l de suco natural
Em sala de aula, a turma será organizada em equipes de quatro estudantes. Estes devem construir as embalagens dos cinco (ou mais) produtos escolhidos pelo professor utilizando as planificações oferecidas. Sugere-se uma parceria com o professor responsável pela disciplina de educação artística para a confecção destas embalagens, ou uma aula de geometria para preparar o material (onde a observação dessas figuras geométricas pudesse contemplar algum conteúdo, por exemplo, recordar quais são as propriedades das figuras tridimensionais). Os estudantes fixam em cada embalagem o seu preço utilizando etiquetas adesivas. As embalagens devem ser dispostas numa prateleira ou então numa área plana grande o suficiente para que seja possível visualizar os preços e quantidades disponíveis.
5ª Etapa: Ação
O professor deve desafiar cada equipe, uma por vez, a escolher produtos que satisfaçam a lista de compras de forma mais econômica possível. Cada equipe anota os produtos que escolheu numa folha de papel e entrega para o professor. Finalmente, o professor lê os resultados e anuncia a equipe que conseguiu economizar mais. Agora os resultados devem ser socializados com o apoio do quadro negro. O professor deve, com a participação dos estudantes, discutir a escolha de cada grupo no momento de decidir suas compras. A discussão deve ser mediada pelas ferramentas apresentadas na 2ª etapa deste plano de aulas, até que toda a turma esteja satisfeita sobre qual seriam as escolhas mais conscientes a se fazer nesta situação.
Materiais Relacionados
1 – Caso você deseje um resumo dos conceitos de razão e proporção, visite o site
2 – Se quiser ver um resumo dos conceitos de razão e proporção com exercícios resolvidos, acesse o link
3 – Para assistir à uma aula completa sobre razão e proporção com exercícios resolvidos, assista ao vídeo Proporcionalidade – Razão e Proporção (Parte 1) | MAB #57

