Conteúdos
Experimentos aleatórios
Objetivos
Competência de área 7 – Compreender o caráter aleatório e não determinístico dos fenômenos naturais e sociais e utilizar instrumentos adequados para medidas, determinação de amostras e cálculos de probabilidade para interpretar informações de variáveis apresentadas em uma distribuição estatística.
H29 – Utilizar conhecimentos de estatística e probabilidade como recurso para a construção de argumentação.
Antes de dar início às Etapas, acesse a aba Para Organizar seu Trabalho e Saber Mais.
1ª Etapa: Introdução ao Tema - experimento
Para introduzir o conteúdo de probabilidade, é interessante propor um jogo que, além de utilizar os conceitos relacionados ao conteúdo, possua regras simples. Por isso, sugerimos iniciar com um jogo de apostas utilizando dois dados.
Como o jogo funciona?
Em cada rodada, os alunos do grupo devem apostar em um número entre 1 e 12. Isso mesmo, o número um entra nas apostas! Apesar de ser impossível chegar a esse valor na soma dos números obtidos no lançamento de dois dados, é importante que os alunos cheguem a essa conclusão sozinhos.
Dois alunos não devem apostar em um mesmo número. Por isso, sugira uma ordem para que eles apostem, alternando o primeiro aluno a falar sua aposta. Você pode propor que o aluno mais novo diga a primeira aposta, e a cada nova rodada, o aluno a esquerda inicie.
Em seguida, um dos alunos lança os dois dados (sugira que o lançamento também seja alternado entre os alunos). O valor obtido é o resultado da soma dos números obtidos nos dois dados.
Ganha o jogador que acertar a soma obtida nos dados.
Divida os alunos em grupos com cinco integrantes, entregue dois dados e uma folha onde eles devem registrar os valores que saírem e as apostas que cada aluno fizer. Veja o exemplo abaixo.
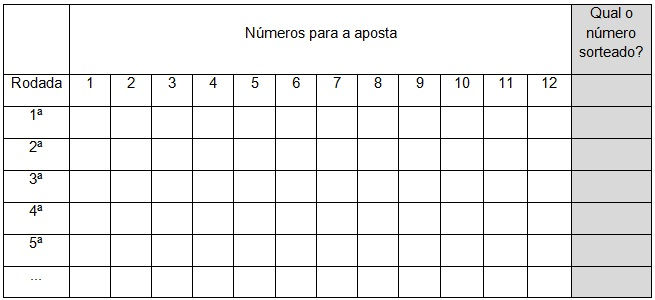
Comece a aula explicando o jogo aos alunos. É interessante fazer uma simulação. Você pode escolher quatro alunos, além de você, e pedir para que escolha um número para a aposta. Escreva os nomes (ou as iniciais dos nomes) dos apostadores na tabela. Se o aluno A escolher 3, o aluno B escolher 7, o aluno C escolher 10, o aluno D escolher 4 e o professor escolher 12, a tabela ficará assim:
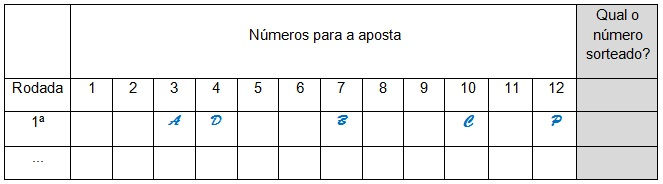
Em seguida, um dos jogadores lança os dois dados soma os valores obtidos.

Neste exemplo, obtemos soma 7. Logo o aluno B ganhou a aposta. Instrua os alunos a anotarem o valor sorteado na tabela, veja abaixo.

Pergunte aos alunos “qual é o melhor número para se apostar nesse jogo” e deixe-os jogar. Peça que joguem ao menos 10 rodadas. Em geral, os alunos se envolvem na atividade e acabam jogando muito mais, por isso, deixe espaço na folha para que registrem outras rodadas.
2ª Etapa: Sistematização do experimento
Depois que os grupos registrarem as apostas e definirem o jogador vencedor pergunte qual o pior valor para se apostar. Geralmente, os alunos falam que o número um é a pior aposta, pois não é possível obter soma um no lançamento de dois dados.
Volte à pergunta inicial: qual é o melhor número para se apostar nesse jogo? Nesse momento, espera-se que os alunos apontem o número obtido com maior frequência durante o jogo. Por isso, os grupos provavelmente apontarão valores diferentes.
Registre na lousa a quantidade de vezes que cada soma foi obtida.
Veja o exemplo abaixo:
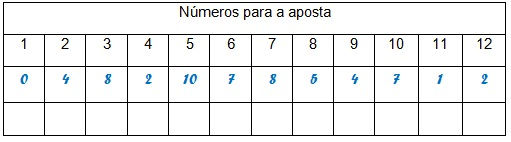
Nesse exemplo, é provável que os alunos apontem o 5 como a melhor aposta, pois essa soma foi obtida no maior número das rodadas.
Por isso, conduza a discussão questionando sobre as possibilidades de se obter soma 5 no lançamento de dois dados. Provavelmente o alunos indicarão apenas duas possibilidades, sair 1 e 4 ou então 2 e 3. Explique há 4 possibilidades: sair 1 no primeiro dado e 4 no segundo, sair 4 no primeiro dado e 1 no segundo; sair 2 no primeiro dado e 3 no segundo; e finalmente, sair 3 no primeiro dado e 2 no segundo.
Vamos registrar os valores como (1º dado; 2º dado), logo, a soma cinco é obtida nos casos (1, 4), (4, 1), (2, 3) e (3, 2).
Junto com os alunos registre todas as possibilidades no quadro. Uma forma de registro adequada para a discussão foi feita a seguir:
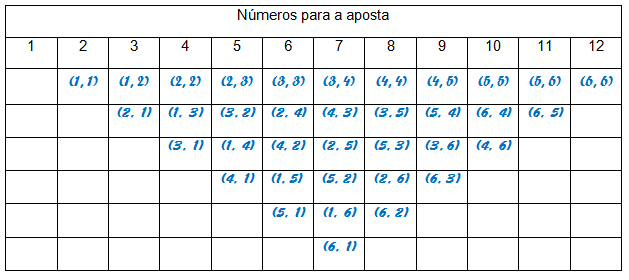
Esse tipo de registro possibilita uma visualização rápida da melhor aposta para o jogo.
3ª Etapa: Sistematização dos conteúdos abordados
Levante as informações anotadas pelos alunos e esclareça possíveis dúvidas. Em seguida, a partir dos dados recolhidos no jogo, explicite os principais conceitos relacionados, dentre eles:
- O que é um experimento aleatório.
- O que é espaço amostral.
- O que é um evento.
- O que é probabilidade.Exemplifique a probabilidade com alguns cálculos; você pode indicar a probabilidade de obter a soma 7, a probabilidade de obter uma soma par, etc.
Depois da sistematização, proponha situações-problema para que o aluno aplique os conhecimentos trabalhados.
Materiais Relacionados
Material sobre probabilidade.
Link 1: http://www.somatematica.com.br/emedio/probabilidade.php
Link 2: http://www.cienciamao.usp.br/dados/t2k/_matematica_mat2g53.arquivo.pdf
Vídeo intitulado “Coisa de passarinho”
Link 3: http://m3.ime.unicamp.br/portal/Midias/Videos/index.php?url=http://m3.ime.unicamp.br/portal/Midias/Videos/VideosM3Matematica/MatematicanaEscola/CoisadePassarinho/
Livro
MLODINOW, Leonard. O andar do bêbado: como o acaso determina nossas vidas. Rio de Janeiro: Forge Zahar, 2009.
Link 4: http://zahar.com.br/doc/t1008.pdf (O link apresenta um trecho do livro)
Artigo
GRANDO, R. C. Concepções quanto ao uso de jogos no ensino de matemática. Revista de
Educação Matemática, São Paulo: SBEM-SP, v. 10, n. 12, p. 43-50, 2007.

