Conteúdos
– Fórmula do cálculo do diâmetro do planeta Terra
– Apresentação da teoria do formato da Terra plana e suas contradições
– O cálculo de Eratóstenes
Objetivos
– Conhecer a teoria do formato plano do planeta Terra
– Conhecer justificativas matemáticas para o formato esférico do planeta Terra
– Conhecer o método usado por Eratóstenes para medir o raio da Terra
1ª Etapa: Início de conversa
A teoria de que o planeta Terra tem a forma plana ganhou muita força durante o ano de 2017. Grupos nas redes sociais e até mesmo conferências foram organizadas para reunir os adeptos à ideia de que andamos sobre um grande disco plano. Apesar das muitas provas de que o nosso planeta tem formato arredondado, esse tipo de discussão ressurge de tempos em tempos e é um tópico que instiga a curiosidade de todos.
A resposta que os chamados “terraplanistas” questionam já foi dada há muito tempo, há aproximadamente duzentos anos antes de Cristo. O objetivo dessa aula é conhecer como foi calculado o raio da Terra por Eratóstenes e apresentar o modelo da Terra plana e suas contradições em relação ao que a ciência já provou.
2ª Etapa: Motivação dos estudantes e diagnóstico do conhecimento prévio
O (A) professor (a) poderá abrir a discussão por meio do diálogo com o grupo.
– Qual o formato do nosso planeta?
– Se é arredondado, como é que não “caímos” para fora dele? Se fosse plano, como perceberíamos isso?
Esse diálogo com o grupo abrirá a discussão que deverá levantar vários tipos de argumentos. O(A) professor(a) poderá alimentar o debate e direcionar a discussão para que os argumentos apresentados tenham uma justificativa científica plausível.
3ª Etapa: O modelo da Terra plana
Aqui, será útil o uso de imagens projetadas ou impressas. Caso não seja possível, recomenda-se que o (a) professor (a) faça um esboço do modelo de Terra plana. Veja desenhos para buscar inspiração.
Além dos desenhos, o (a) professor (a) poderá encontrar outras figuras nos links indicados em “Materiais Relacionados” ou em uma rápida busca no Google Imagens, usando o termo “Terra plana”.
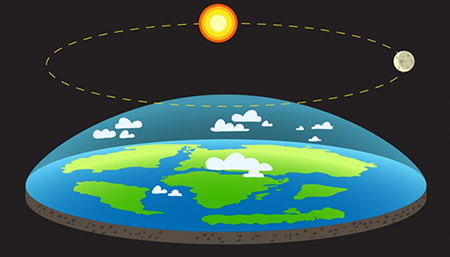
No modelo de Terra plana, Sol e Lua são esferas bem menores do que a Terra, que percorrem nossa atmosfera por meio de movimentos circulares. Além disso, a gravidade como conhecemos não existe, ela é apenas uma força misteriosa que atrai tudo diretamente para baixo, em direção ao solo. Por fim, a Antártida é um paredão de gelo intransponível que contorna todo o disco do nosso planeta.
Com essa breve descrição, o grupo já deve estar pronto para refletir sobre o modelo. O (A) professora (a) irá provocar a imaginação dos estudantes com a seguinte discussão:
Observe as figuras apresentadas e reflita pensando no modelo de Terra plana:
a) Como aconteceria um eclipse solar?
b) Ao ver um barco desaparecer no horizonte, nota-se que ele parece “afundar” na linha do horizonte. Qual seria a explicação para esse fenômeno?
c) Por que a região do Equador é a mais quente do nosso planeta?
Essas perguntas são impossíveis de responder utilizando o modelo de Terra plana, pois esse não é um modelo válido. O (A) professor (a) deverá enfatizar isso e discutir as questões sugeridas demonstrando como o modelo da Terra esférica torna possível um eclipse solar, o desaparecimento do barco no horizonte dando a impressão de que está afundando e a temperatura mais elevada da região do Equador. Nosso planeta tem formato arredondado, aproximadamente esférico, e será apresentado quem foi um dos primeiros cientistas a registrar essa observação.
4ª Etapa: A ideia de Eratóstenes
Eratóstenes foi um dos primeiros cientistas a calcular o raio do planeta Terra. Além de matemático, ele é conhecido como o criador da disciplina geografia. Seu feito data de 240 anos antes de Cristo.
Para esse tópico, será interessante usar uma projeção ou impressão de mapas, destacando a cidade de Siena (atual Assuão) e de Alexandria, no Egito. O (A) professor (a) poderá utilizar o Google Maps ou mesmo um atlas.
Eratóstenes descobriu que na cidade de Siena, localizada ao sul do Egito, durante o solstício de verão, o sol posicionava-se de tal forma que um bastão colocado perpendicularmente em relação ao solo não possuiria sombra. No entanto, ao mesmo tempo, em Alexandria um bastão com o mesmo formato colocado perpendicularmente em relação ao solo produzia sombra. Eratóstenes percebeu que a única explicação para esse fenômeno seria a existência de um ângulo entre os dois bastões e deduziu que poderia calcular o raio da Terra utilizando grandezas, razão e proporção.
O (A) professor (a) poderá utilizar-se do quadro para ilustrar esse fenômeno.
5ª Etapa: Como calcular o raio da Terra?
Eratóstenes compôs a seguinte fórmula, utilizando a geometria de grandezas diretamente proporcionais:
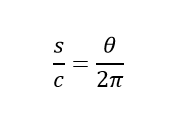
Onde S é a distância entre Siena e Alexandria, C o diâmetro do planeta Terra e θ é o ângulo entre os dois bastões.
Utilizando o tamanho da sombra do bastão, em Alexandria, e a trigonometria, ele calculou θ e então contratou uma pessoa para medir a distância entre Siena e Alexandria, com o propósito de concluir qual era o diâmetro do planeta Terra.
6ª Etapa: Exercícios
Imaginaremos que estamos agora no lugar de Eratóstenes e realizaremos alguns cálculos com os alunos usando uma calculadora científica.
Exercício 1: Suponha que o bastão, em Alexandria, possui 10 metros de comprimento e produz uma sombra de aproximadamente 1,584 metros. Qual será o ângulo entre os dois bastões θ? (Dica: utilize uma calculadora científica com a função tangente).
R: Aproximadamente 9 graus.
Exercício 2: Sabendo que a distância entre Siena e Alexandria é de aproximadamente 1.000 km, estime qual é o tamanho do diâmetro do planeta Terra.
R: Aproximadamente 40.000 km.
Por meio das discussões, análise das teorias e exercícios propostos, chegaremos à conclusão de que a Terra possui uma forma aproximadamente esférica.
Materiais Relacionados
1 – Recomenda-se que o (a) professor (a) acesse algum material preliminar para conhecer um pouco mais a respeito da recente discussão sobre a Terra ser plana. Veja esse artigo informativo. Acesso em 16 de março de 2018.
2 – Sugere-se, também, a leitura do artigo “Como seria o mundo se a Terra fosse realmente plana, segundo a ciência”, que trata sobre as consequências de um formato plano para o nosso planeta. Acesso em 16 de março de 2018.
3 – É necessário que exista pelo menos uma calculadora científica à disposição.

