Conteúdos
– Números inteiros
– Operações básicas
Objetivos
– Conhecer as ideias relacionadas aos números inteiros
– Realizar as operações básicas com números inteiros
Previsão para aplicação:
4 aulas (50 min/aula)
1ª Etapa: Conhecendo os números inteiros
É comum os estudantes encontrarem dificuldades ao estudarem Números Inteiros, principalmente devido à barreira imposta pela parte negativa desses números. Enquanto os valores positivos são de fácil relação com a realidade à nossa volta, os números abaixo de zero necessitam de maior abstração para entender de que modo eles podem quantificar fenômenos físicos e apoiar atividades cotidianas. Com o intuito de contornar este obstáculo, este plano de aula buscará mostrar este conteúdo relacionando-o com aplicações reais e utilizando materiais concretos. Indicamos principalmente para o 7º ano, série em que a matéria é abordada, podendo ser aplicado também no 8º ano.
Os Números Inteiros são formados pelos Números Naturais e seus opostos (os negativos), incluindo o zero. Por exemplo, o número 1 é um número natural, e o seu oposto é o -1. O número 2 é um número natural, e o -2 é seu oposto, e assim por diante. O conjunto dos Números Naturais geralmente é representado pela letra N:
N = {0, 1, 2, 3, 4, 5…}
Os opostos seriam então: { -1, -2, -3, -4, -5, -6…}
Juntando esses dois conjuntos, temos o conjunto dos Números Inteiros, geralmente representado pela letra Z:
Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4…}
Após fazer essa explicação inicial, para que os estudantes compreendam a natureza dos Números Inteiros e a relação entre eles, pode utilizar algumas aplicações, como por exemplo, o termômetro e a medição da temperatura em graus Celsius. Inicie um debate com a turma a respeito da temperatura local. Segue algumas perguntas para orientar a conversa:
Qual a temperatura agora? (Pode-se consultar a Internet para conferir a temperatura real)
Qual cidade é mais fria que essa? Qual é mais quente?
Qual a temperatura no polo norte? E no deserto do Saara?
Procure chegar a temperaturas próximas as reais e utilize exemplos que possuam temperaturas negativas. A intenção é que os alunos percebam que todos os números negativos são menores que zero e que -20 é menor que – 10, por exemplo. Em seguida, relacione com a reta numérica:
![]()
Desenhe a reta numérica na lousa e posicione as temperaturas das cidades encontradas. Mostre que escolhendo um número qualquer da reta, os números a esquerda dele são menores que ele e os à direita são maiores.
Por fim, peça que os alunos em duplas resolvam o problema que segue:
1) Sete pessoas viajaram nas férias para sete cidades diferentes. Cada uma delas registrou a temperatura que estava marcando no momento que chegou ao destino. Com essas informações foi possível montar a seguinte tabela:
| Nome | Cidade | Temperatura |
|---|---|---|
| Paula | Belo Horizonte | 25º C |
| Rafaela | Porto | 6 C |
| Leandro | Estocolmo | -20º C |
| Joaquim | Luanda | 32º C |
| Ana | Montevideo | 0º C |
| Pedro | Joanesburgo | 12º C |
| Maria | Quebec | -15º C |
a) Em qual país fica cada uma dessas cidades?
b) Qual cidade registrava a maior temperatura? E qual cidade registrava a menor?
c) Coloque as temperaturas em ordem crescente. Em seguida, coloque as temperaturas em uma reta numérica.
Para reforçar o entendimento, pode-se discutir outro exemplo de utilização de números inteiros: a altitude medida em metros. O nível do mar é considerado como a altitude zero, portanto, o que está acima do nível do mar tem altitude positiva e o que está abaixo do nível do mar tem altitude negativa. Por exemplo, o Monte Everest é o ponto mais alto do mundo e está a cerca de 8450 m de altitude. Já as Fossas Marianas são o ponto mais baixo da Terra, estando a uma altitude de cerca de -11.000 m. Inicie um debate questionando qual a altura da cidade que vivem e comparem com outras.
Para finalizar, passe uma tarefa na qual os estudantes devem pesquisar dois locais na Terra, um com altitude positiva e outro com altitude negativa.
2ª Etapa: Operações com números inteiros
Para abordar as operações com números inteiros utilizaremos um material concreto. Serão necessárias dezenas de palitinhos pintados de vermelho e de azul. Podem ser palitos de sorvete, e considere 20 palitos de cada cor por dupla de alunos. Também é possível fazer com canudos, ou qualquer outro material que considerar conveniente.
Explique que cada palitinho azul vale +1 e cada palitinho vermelho vale -1. Ao juntar dois palitos de cores diferentes eles se anulam, e será esse o raciocínio para realizar operações de soma e subtração. Faça alguns exemplos na lousa:

Exemplo usando apenas números naturais: 3 + 4 = 7.
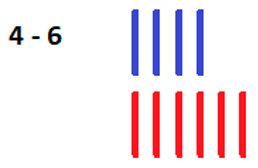
Nesse exemplo temos 4 positivos e 6 negativos. Explique que quando o sinal está oculto consideramos como positivo. 4 positivos irão anular 4 negativos e irá sobrar 2 negativos: 4 – 6 = -2.
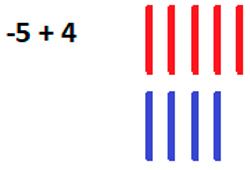
No terceiro exemplo, temos 5 negativos e 4 positivos, fazendo a compensação, restará 1 negativo: -5 + 4 = -1.

Por fim, uma conta só com negativos resulta em negativos: -2 – 4 = -6.
Após resolver diversos exemplos e tirar as dúvidas, passe uma lista de exercícios para que os estudantes resolvam em duplas, com o auxilio dos palitos coloridos.
1) -7 + 3
2) -8 – 3
3) 9 – 5
4) -6 + 11
5) 8 – 12
6) 6 + 12
7) -10 + 9
8) 7 – 13
Para que a partir do material concreto utilizado eles relacionem com a realidade, apresente outro contexto onde são utilizados os números negativos: saldo de conta bancária. Quando o saldo de uma conta esta positivo significa que temos crédito, quando está negativo, estamos em débito (estamos devendo) com o banco. Escolha alguns exemplos para relacionar com essa conjuntura:
1) 3 + 4: imaginem que temos 3 reais de saldo e depositamos mais 4 reais, ficaremos com 7 reais na conta: 3 + 4 = 7.
2) 4 – 6: temos 4 reais de saldo e pagamos uma conta que vale 6 reais, ficaremos devendo 2 reais: 4 – 6 = -2.
3) -5 + 4: estamos com saldo negativo de 5 reais no banco, depositamos 4 reais, e o saldo continua negativo de -1 reais: -5 + 4 = -1
4) -2 – 4: o saldo está negativo em – 2 reais, pagamos uma conta de 4 reais, e ficamos devendo 6 reais: -2 – 4 = -6.
Esta abordagem é interessante para tratar de alguns conceitos relacionados com Matemática Financeira e do funcionamento de contas bancárias. Segue um exercício que dialoga com isto, e que pode servir como tarefa para casa:
1) A tabela que segue é um extrato de conta bancária. O sinal positivo dos números da coluna “Movimentação” indica que foi feito um depósito e os sinais negativos indicam que foi feito uma retirada de dinheiro. Qual o saldo da conta em 20 de feveiro de 2018?
| Data | Tipo | Movimentação (R$) | Saldo (R$) |
|---|---|---|---|
| 01/02/2018 | 50 | ||
| 10/02/2018 | Depósito | 25 | 75 |
| 15/02/2018 | Pagamento aluguel | -100 | |
| 20/02/2018 | Depósito | 41 |
Materiais Relacionados
Para acessar o conteúdo de números inteiros:
1) Conteúdo “O que é o conjunto dos números inteiros?”, site Brasil Escola. Acesso em: 03 de novembro de 2019.
2) Conteúdo “Números inteiros”, site Toda Matéria. Acesso em: 03 de novembro de 2019.
Para ver o conteúdo em livro didático:
BIGODE, Antônio José Lopes. Matemática no Cotidiano. São Paulo: Editora Scipione, 2015.

