Conteúdos
Fazendo uso de metodologias ativas, este plano de aula tem como objetivo explicar o que é o Teorema de Tales e quais são as suas aplicações.
Objetivos
- Compreender o enunciado do Teorema de Tales; e
- Identificar e aplicar o teorema em situações geométricas.
Conteúdos/Objetos do conhecimento:
- Teorema de Tales;
- Proporcionalidade; e
- Paralelismo entre retas em uma figura geométrica.
Palavras-chave:
Teorema de Tales.
Previsão para aplicação:
3 aulas (50 min/aula).
1ª Etapa: O que é o Teorema de Tales?
Comece a aula perguntando aos alunos se eles já ouviram falar em teorema de Tales.
Apresente à turma imagens ou objetos do cotidiano, como sombras projetadas, pontes ou grades, para destacar relações proporcionais e pergunte: “Como conseguimos calcular a altura de um objeto usando apenas a sua sombra?” ou “Vocês conseguem identificar proporções entre os objetos mostrados?”.
2ª Etapa: Exposição teórica
Para dar início a esta etapa, explique aos alunos o conceito de proporcionalidade em segmentos de reta.
Mostre o enunciado do Teorema de Tales: “Se duas retas paralelas são cortadas por duas transversais, então os segmentos determinados em uma transversal são proporcionais aos segmentos correspondentes da outra”. Dê um exemplo de um gráfico simples, no quadro ou em projeção.
Como continuação, passe aos alunos um exercício prático e distribua folhas com desenhos de triângulos formados por retas paralelas e transversais. Oriente os alunos que identifiquem as proporções entre os segmentos e confirmem o teorema.
3ª Etapa: Aplicação prática e resolução de problemas
Partindo das descobertas ocorridas na etapa anterior, aplique problemas práticos e contextualizados para ajudar os alunos na correlação entre teoria e prática, contribuindo para consolidar o seu aprendizado.
- Exercícios contextualizados: Peça aos alunos que calculem a altura de um poste, com base na sombra de uma vara de madeira e de seu próprio comprimento.
Exemplo 1 : João quer saber a altura de um poste, mas não tem uma trena longa o suficiente. Ele finca uma vara de 1 metro no chão e mede sua sombra, que tem 0,5 metro. A sombra do poste mede 4 metros. Qual é a altura do poste?
Para resolver o exercício, utilize a relação proporcional entre os segmentos:
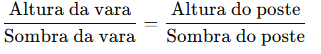
Exemplo 2: Você está de frente para um rio e precisa saber a largura dele sem atravessá-lo. Em um ponto fixo da margem, você caminha 5 metros para a direita e coloca uma estaca. Depois, anda mais 10 metros para a direita e posiciona outra estaca. A partir da última estaca, você observa que o alinhamento entre as duas estacas e um ponto fixo na margem oposta forma um triângulo proporcional. A distância entre as duas estacas na margem oposta é de 6 metros. Qual é a largura do rio?
Exemplo 3: Uma lâmpada está fixada no teto, a 2,5 metros de altura, e um objeto de 1 metro de altura está colocado a 1 metro da parede. A sombra projetada na parede mede 2 metros. Qual é a distância da lâmpada até a parede?
Exemplo 4: Um fotógrafo está em pé a 1,8 metro de altura e quer estimar a altura de uma torre de igreja. Ele sabe que a sombra dele mede 0,9 metro e que a sombra da torre mede 15 metros. Qual é a altura da torre?
Exemplo 5: Um arquiteto quer fazer a maquete de uma ponte em escala. A ponte real tem 150 metros de comprimento, e ele quer representar na maquete usando 15 centímetros. Uma viga da ponte tem 50 metros na realidade. Qual será o tamanho dessa viga na maquete?
- Atividade em grupo: com a turma dividida em grupos, passe uma lista de exercícios diferente para cada um deles. Estimule a competitividade entre grupos e dê uma recompensa ao grupo que mais acertar questões e terminar antes.
Bom trabalho!
Plano de aula elaborado pela Professora Gabriela Ribeiro do Prado.
Coordenação Pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.
Revisão textual: Professora Daniela Leite Nunes.
Crédito da imagem: Klaus Vedfelt – Getty Images

