Conteúdos
Este plano de aula tem como foco o trabalho com simetria, fundamental para a compreensão de diversos conceitos geométricos e de movimentos no plano e no espaço. Nos anos iniciais do ensino fundamental é esperado que os/as estudantes reconheçam simetria de reflexão em figuras e em pares de figuras geométricas planas e façam uso desse conceito na construção de figuras congruentes, com o uso de malhas quadriculadas ou de softwares de geometria.
A proposta é trabalhar de forma significativa o desenvolvimento da capacidade da estimativa visual, percepção espacial, capacidade de observar o que está ao redor e de perceber a natureza das formas. As aulas poderão favorecer aprendizagem de conceitos matemáticos e geométricos por meio da manipulação de representações de figuras geométricas planas em quadriculados ou no plano cartesiano.
Objetivos
- Compreender a simetria como fenômeno presente na natureza.
- Identificar simetria em elementos reais (objetos, plantas, animais).
- Desenvolver noções de plano cartesiano e de coordenadas cartesianas.
- Construir figuras simétricas.
Conteúdos/Objetos do conhecimento:
- Simetrias de figuras planas (reflexão e rotação).
- Eixo de simetria.
- Localização e movimentação no plano cartesiano.
Palavras-chave:
Simetria; Figuras planas; Figuras simétricas; Eixo de simetria; Plano cartesiano; Malha quadriculada.
Previsão para aplicação:
2 aulas (50 min).
1ª Etapa: Levantando os conhecimentos
Comece levantando os conhecimentos prévios da turma para verificar o que sabem sobre simetria e questione:
- Onde podemos encontrar simetrias?
Apresente uma figura simétrica e pergunte:
- O que acontece com a figura quando a dobramos sobre o eixo?
- As duas partes da figura ficam exatamente iguais?
Apresente outra figura simétrica e pergunte:
- Onde está o eixo de simetria nesta figura?
2ª Etapa: Exploração
Para essa etapa, será preciso que você, professor/a, leve os/as estudantes a um espaço aberto da escola onde seja possível encontrar elementos da natureza (ou traga para a aula elementos naturais previamente coletados).
Peça que observem folhas, flores e outros elementos.
Questione:
- “Vocês percebem que, se passarmos uma linha ao meio, alguns desses elementos são iguais dos dois lados?”
- “As folhas são simétricas?”
A proposta é que, ao explorar o espaço e os elementos naturais, os/as estudantes percebam semelhanças e diferenças identificando as regularidades geométricas.

Explique sobre a simetria de reflexão: quando uma figura pode ser dividida em duas partes iguais, que são imagens espelhadas uma da outra. O eixo de simetria é uma linha, real ou imaginária, que atravessa o centro da figura. Exemplos: borboleta, coração, letra A.
Apresente imagens de azulejos (como os das imagens a seguir, de estilo português) e peça para que observem e analisem com calma a simetria de cada um – por exemplo:

Estimule para que imaginem uma linha passando bem ao meio de cada figura. Espera-se que os/as estudantes reconheçam intuitivamente o conceito de simetria.
Mostre imagens de construções simétricas, por exemplo, o Taj Mahal:

Fonte: https://whc.unesco.org/en/list/252/
Explique que o Taj Mahal é um edifício simétrico perfeito, com ênfase na simetria bilateral ao longo de um eixo central, no qual se distribuem os principais elementos.
Questione os/as estudantes sobre o conceito do eixo de simetria e onde podemos encontrar este eixo na natureza, na arquitetura, nas obras artísticas. Após ouvi-los/as, mostre outras imagens para que encontrem o eixo de simetria.
3ª Etapa: Resolução de situação problema em grupo
Organize a turma em pequenos grupos e proponha a resolução de um problema, por exemplo:
“A prefeitura de uma cidade renovou toda a frota de ambulâncias. Para facilitar a identificação desses veículos nas ruas, a pessoa responsável pelo setor solicitou que a palavra RESGATE fosse pintada na parte da frente das ambulâncias. Assim, ao ver o veículo se aproximando pelo retrovisor, qualquer motorista possa reconhecer rapidamente que se trata de uma ambulância e abrir caminho. Para que isso aconteça, de que forma a palavra RESGATE deve ser escrita na parte da frente da ambulância, de modo que a motorista à frente consiga lê-la corretamente no espelho retrovisor?”
Dê um pedaço de papel para cada grupo, para que escrevam a palavra usando o princípio da simetria.
Ao final, abra espaço para uma conversa coletiva, para que os grupos apresentem suas respostas. A ideia é que os/as estudantes percebam a inversão provocada pela simetria de reflexão e associassem a palavra que deveria ser escrita na parte frontal da ambulância à sua imagem em um espelho.
4ª Etapa: Produção em duplas
Apresente uma malha quadriculada com dois eixos perpendiculares (horizontal e vertical), indicados com linhas mais acentuadas, formando um quadrante.
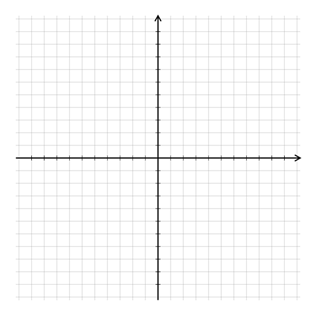
Peça para os/as estudantes construírem uma figura no primeiro quadrante. Após a criação do desenho, peça para que os/as estudantes desenhem uma imagem simétrica em relação ao eixo vertical.
Depois, solicite que desenhem uma imagem simétrica ao eixo horizontal.
Converse com a turma sobre o que ocorre com uma figura ao se aplicar sucessivamente duas simetrias de reflexão com eixos perpendiculares. Pergunte: ‘O que vocês observaram nas construções das figuras simétricas em relação aos eixos de simetria vertical e horizontal? Espera-se que percebam que isso equivale a uma simetria de rotação de 180º em relação ao ponto de encontro dos eixos.
A simetria rotacional (ou central) acontece se, ao girar uma figura ao redor de um ponto, ela fica exatamente como na posição original. Ou seja, a aparência do objeto não muda mesmo depois da rotação.
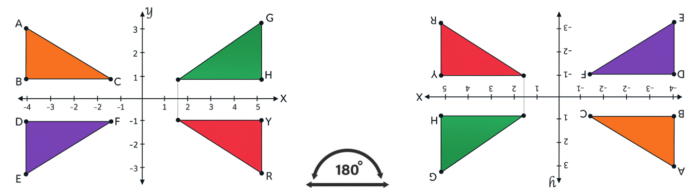
Outras possibilidades:
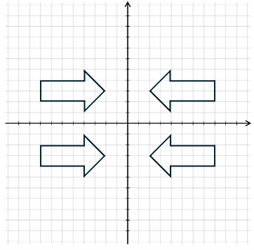
5ª Etapa: Finalização
Realize a sistematização das ideias e reforce que a simetria é utilizada na matemática, na geometria, na gramática, na arte, na natureza e na arquitetura. Na biologia, por exemplo, a simetria consiste na correspondência ideal do corpo de uma planta ou animal em relação a um centro, um eixo ou um plano. Na gramática, a simetria é a correspondência regular entre os elementos da frase. A simetria na arquitetura passa uma sensação de segurança e estabilidade, além de criar um senso de proporção. Esteticamente, a simetria é atraente e muito relacionada à beleza. É possível perceber na natureza vários padrões simétricos, como as colmeias das abelhas, a pele das cobras, o casco da tartaruga. A simetria está presente nas obras de arte, nas construções, nos móveis, nos mais diversos objetos do cotidiano.
Reforce os principais conceitos.
- Simetria de reflexão: A figura é “espelhada”.
- Simetria de rotação: É quando uma figura pode ser girada (rotacionada) em torno de um ponto fixo e ainda coincidir com ela mesma antes de completar uma volta total.
Faça perguntas para retomar os conceitos e avaliar as aprendizagens:
- Qual tipo de simetria é mais fácil de identificar: reflexão ou rotação? Por quê?
- Onde encontramos simetrias no nosso cotidiano (em objetos, natureza, arquitetura)?
Bom trabalho!
Plano de aula elaborado pela Professora Renata Helene Ferreira Campos.
Coordenação Pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.
Crédito da imagem: MarinaRazumovskaya – Getty Images

