Conteúdos
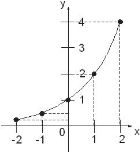
Função exponencial.
Objetivos
• Ler e interpretar textos de Matemática.
• Ler, interpretar e utilizar representações matemáticas (tabelas, gráficos, expressões etc).
• Transcrever mensagens matemáticas da linguagem corrente para linguagem simbólica(equações, gráficos, diagramas, fórmulas, tabelas etc.) e vice-versa
• Identificar o problema (compreender enunciados, formular questões etc).
• Procurar, selecionar e interpretar informações relativas ao problema.
• Formular hipóteses e prever resultados.
1ª Etapa: Introdução ao tema.
Inicie a atividade propondo para os alunos resolvam em grupos alguns desafios que envolvam funções exponenciais.
Como exemplo, sugerimos os seguintes desafios:
Um jogador da Mega Sena ganhou sozinho R$ 1.000.000,00 (um milhão de reais). Ele pretende aplicar todo esse dinheiro na poupança, com um rendimento de 10% ao mês. Considerando que ele irá sacar esse dinheiro somente após 1 (um) ano de aplicação, quanto dinheiro ele terá?
f(x) = total de dinheiro que terá daqui a 1 ano
a = base = rendimento mensal somado ao valor inicial = 10% + 100% = 0,1 + 1 = 1,1
x = expoente = número de meses da aplicação = 1 ano = 12 meses
f(x) = 1000000 . ax
f(x) = 1000000 . 1,112
f(x) = 1000000 . 3,138
f(x) = 3,138000
Assim, após um ano de aplicação, o apostador terá R$ 3.138.000,00 (três milhões e cento e trinta e oito mil reais).
Um casal resolveu comprar uma casa no valor de R$ 350.000,00 (trezentos e cinqüenta mil reais). Como não possuíam o dinheiro para pagar à vista, fizeram um financiamento de R$ 200.000,00 (duzentos mil reais). Os juros do financiamento são de 20% ao ano. Eles pretendem pagar a casa em 10 anos. Qual será o valor final do financiamento da casa?
f(x) = valor total a ser pago pelo financiamento daqui a 10 anos
a = base = juros anual somado ao valor inicial = 20% + 100% = 0,2 + 1 = 1,2
x = expoente = período de financiamento = 10 anos
f(x) = 200000 . ax
f(x) = 200000 . 1,210
f(x) = 200000 . 6,192
f(x) = 1,238400
Assim, após 10 anos, o valor pago pelo financiamento será de R$ 1.238.400,00 (um milhão, duzentos e trinta e oito mil e quatrocentos reais).
Numa área de preservação ambiental, para que uma espécie de planta não fosse extinta, pesquisadores mantiveram sob cuidados o último exemplar dessa espécie. Sabendo que uma planta dessa espécie gera 10 mudas por ano (que são capazes de se reproduzir após um ano) e logo em seguida morre, e sabendo que seria necessário, no mínimo, 10.000 exemplares para garantir que a espécie não corra mais risco de extinção, será que após 5 anos a espécie não precisará mais de acompanhamento porque saiu do risco de extinção?
f(x) = número de exemplares da planta
a = base = número de descendentes gerados a cada ano, por planta = 10
x = expoente = número de períodos de tempo (ano) considerado = 5
f(x) = ax
f(x) = 105
f(x) = 100000
A resposta é sim, pois após 5 anos, existirão 100.000 (cem mil) exemplares da planta, e por isso a espécie não correrá mais risco de extinção e não precisará de acompanhamento.
Acompanhe os grupos durante a resolução e peça que compartilhem não somente os resultados, mas a forma que utilizarão para resolver. Pode ser que os alunos expliquem de formas diferentes a resolução de um mesmo desafio. Procure observar e valorizar estes processos.
Certifique-se de que todos os alunos tenham compreendido os conceitos envolvidos na atividade.
2ª Etapa: Exploração da atividade interativa.
Organize a turma em duplas de trabalho para utilização de computadores portáteis ou dos computadores da sala de informática.
Peça para que os alunos acessem a atividade interativa “Função Exponencial”, disponível no site NET Educação (material de apoio).
Após a exploração, certifique-se que os alunos compreenderam o desafio do jogo de xadrez e motive-os a pensarem em duplas a respeito as estratégias que deverão utilizar para resolução dos desafios.
Pergunte se eles acreditam que os conceitos envolvidos nas aulas de matemática poderão ajuda-los na resolução. Certamente algum aluno citará as funções exponenciais e caso ninguém comente, relembre com eles o que foi abordado na primeira etapa da atividade deste plano.
Ao término da atividade interativa, discuta com os alunos os resultados e as estratégias que utilizaram para resolver o desafio.
Essa atividade interativa apresenta uma lenda de um rei, que cansado da monotonia do reino, pede para que um de seus súditos lhe desenvolva um jogo. Como pagamento, o inventor do xadrez pediu para que em, cada uma das 64 casas do tabuleiro fossem colocadas moedas de ouro, na seguinte condição: na primeira casa deveria ser colocada uma moeda e nas demais casas deveria ser colocado o dobro de moedas que havia na casa anterior. Essas moedas, então, seriam seu prêmio pela invenção. Para resolver esse e outros desafios do nosso cotidiano, os alunos terão de compreender os conceitos e as formas de resolução das funções exponenciais.
3ª Etapa: Retomada Conceitual
Após a realização da atividade interativa, disponibilize para turma alguns situações que envolvem funções exponenciais e proponha que a sala, divida em trios expliquem porque elas tratam desse tipo de funções.
Como exemplo sugerimos as seguintes situações:
Exemplo 1
(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo
R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
Resposta: A máquina foi comprada pelo valor de R$ 48.000,00.
Exemplo 2
(EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares?
Use 1,0320 = 1,80.
Temos a seguinte função exponencial:
P(x) = P0 * (1 + i)t
P(x) = 500 * (1 + 0,03)20
P(x) = 500 * 1,0320
P(x) = 500 * 1,80
P(x) = 900
Resposta: O PIB do país no ano de 2023 será igual a R$ 900 bilhões.
Posteriormente, oriente os grupos a criarem 1 desafio que envolva, em sua resolução, os conteúdos trabalhados na atividade interativa. Se a aprendizagem conceitual foi garantida nas etapas anteriores, os alunos só precisarão usar a criatividade para elaborar desafios interessantes.
Sugira que os alunos troquem os desafios entre os grupos para que sejam solucionados, de modo que cada grupo terá que solucionar 1 desafio diferente do que foi criado. Posteriormente, oriente que cada grupo exponha para a turma os desafios e as estratégias utilizadas nas respectivas resoluções.
Materiais Relacionados
Caro professor, antes de iniciar esta atividade é importante que se aproprie de algumas informações sobre o tema. Selecionamos os links abaixo para ajudá-lo.
Leia o conteúdo disponível nos links abaixo:
Plano de aula – xadrez exponencial
http://www.inf.unioeste.br/~rogerio/PLANO.DE.AULA-Xadrez-exponencial.pdf
Estudo da função exponencial e a indução matemática com a aplicação da torre de hanói
http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/696-4.pdf
Tendências em matemática – como resolver um problema envolvendo função exponencial.
http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/411-4.pdf