Conteúdos
– Volume de blocos retangulares
– Unidades de medidas de volume
Objetivos
– Conhecer o conceito de volume
– Calcular o volume de blocos retangulares (paralelepípedo reto retângulo)
– Utilizar instrumentos de medição de comprimento (régua e trena)
Previsão para aplicação:
4 aulas (50 min/aula)
1ª Etapa: Introdução ao tema
Este plano de aula é sugerido para o 7º ano, quando os alunos são iniciados ao cálculo de volume, mas também pode ser utilizado nos 8º e 9º anos, séries nas quais este conteúdo é revisitado. Inicialmente, é importante rever o conceito de volume, ideia que terão tido contato em anos anteriores.
Volume geralmente é definido como uma grandeza que corresponde à quantidade de espaço que um corpo tridimensional ocupa. Há algumas estratégias para ajudar os estudantes a compreenderem o conceito de volume e a partir disso pensarem em maneiras de quantificar essa grandeza. Uma possibilidade é levar caixas (no formato de blocos retangulares, também chamados de paralelepípedos reto retângulo) de tamanhos diversos e fazer questões a respeito:
Figura 1: Caixas diversas

Fonte das imagens: Americanas.com e Casa do papelão
– Qual dessas caixas é maior? Qual possui maior volume?
– Como podemos quantificar quanto uma caixa é maior que outra?
– Como podemos calcular o volume de cada caixa?
Após um debate, é possível que surja a ideia de calcular o volume por meio de uma unidade de medida padrão, por exemplo, um cubinho. Pode-se quantificar o volume a partir do número de cubinhos que cabem em cada caixa: a caixa na qual couber mais cubinhos será a maior. Neste momento, uma possibilidade para melhorar o entendimento é fazer um paralelo com as unidades de medida de comprimento e área.
Se o(a) professor(a) tiver acesso aos cubinhos do material dourado, por exemplo, nesse momento pode-se construir blocos diversos, utilizando quantidades diferentes de cubinhos e destacar que o volume de cada bloco montado é igual ao número de cubinhos usado (se considerarmos que o cubinho é a unidade de medida de volume).
Figura 2: Material dourado

Pergunte aos alunos como podemos montar uma expressão matemática para calcular o número de cubinhos de cada bloco e, dessa forma, calcular o volume. A intenção é que eles percebam que se deve multiplicar o número de cubinhos que há nas três dimensões: comprimento, largura e altura.
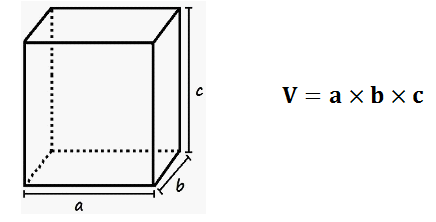
A partir daí é possível fazer uma ponte considerando que cada cubinho tem 1 cm x 1cm x 1cm, ou seja, a unidade de medida de volume seria 1 cm³ e, portanto, para calcular o volume das caixas basta tomar as medidas em cm dos comprimentos das três dimensões.
Figura 3: Fórmula para cálculo do volume de um bloco retangular
2ª Etapa: Construindo caixas
Esta segunda etapa tem como objetivo reforçar o entendimento da fórmula para o cálculo do volume de blocos retangulares. Os estudantes, organizados em grupos, receberão algumas folhas de sulfite. Utilizando régua, tesoura e cola (ou durex) deverão montar pequenas caixas, de modo que elas tenham os volumes definidos pelo(a) professor(a).
Figura 4: Modelo para montar pequenas caixas de papel

Para exemplificar, suponhamos que determinado grupo deverá montar caixas com volumes de 30 cm³, 64 cm³ e 120 cm³. Os estudantes devem compreender que, para produzir a caixa de 120 m³, por exemplo, deverão encontrar três medidas que multiplicadas deem esse valor e que há diversas respostas possíveis: 6 x 4 x 5 cm, 3 x 12 x 5 cm, 6 x 2 x 10 cm, etc. Reforce que para qualquer dessas respostas escolhidas, a caixa produzida terá o mesmo volume, ou seja, caberá a mesma quantidade de cubinhos de 1 cm³. Se tiver cubinhos dessa medida disponíveis, peça aos alunos que coloquem essa quantidade de cubos dentro da caixa.
3ª Etapa: Calculando o volume de caixas
Para a etapa final, peça aos estudantes que tragam diversas caixas de tamanhos variados no formato de blocos retangulares. Organizados em grupos, calcularão o volume de determinada quantidade de caixas utilizando régua ou trena. Para cada caixa, solicite que façam um desenho em papel sulfite colocando as medidas e o cálculo do volume. Será necessário explicar que provavelmente haverão medidas “quebradas” e, portanto, muitas vezes terão que fazer as contas com números decimais.
Para finalizar, proponha um desafio: calcular o volume da sala de aula em m³. Comece explicando a diferença entre m³ e cm³ – como medida de volume. Esse é o momento para apresentar as diversas unidades de medida de volume.
Se for possível e se tiver trenas suficientes, uma possibilidade é pedir que cada grupo estime o volume de algum cômodo diferente da escola. Uma tarefa de casa interessante seria os alunos medirem o volume de algum cômodo de suas casas.
Materiais Relacionados
1) O(A) professor(a) poderá recordar a fórmula para cálculo do volume de blocos retangulares e as unidades de medida de volume nos seguintes links:
– Conteúdo “Volume do paralelepípedo”, do site Mundo Educação. Acesso em: 04 de outubro de 2019.
– Conteúdo “Volume do paralelepípedo, do cubo e do cone”, do site Brasil Escola. Acesso em: 04 de outubro de 2019.
2) O(A) professor(a) poderá aprofundar o conteúdo na seguinte obra:
DOLCE, Osvaldo & POMPEO, Nicolau. Fundamentos de Matemática Elementar: Geometria Espacial. Volume 10. São Paulo: Atual Editora, 2013.

