Conteúdos
Este plano de aula de Matemática aborda o conceito de decomposição de números naturais. O material apresenta o conjunto dos Números Naturais (ℕ), em seguida discute-se o caráter posicional do nosso sistema numérico, para finalmente apresentar o procedimento de decomposição de um número natural. Diversos exemplos resolvidos são tratados ao longo do material, que também conta com algumas sugestões de textos e vídeos (em “Materiais relacionados”), para que o(a) professor(a) possa aprofundar o tema.
- O conjunto dos números naturais;
- Sistema numérico posicional; e
- Decomposição de números naturais.
Objetivos
- Compreender o que são os números naturais;
- Compreender o caráter posicional do nosso sistema numérico; e
- Aprender a decompor números naturais.
Palavras-chave:
Números naturais. Decomposição de números.
Previsão para aplicação:
2 aulas (50 min/aula).
1ª Etapa: O conjunto dos Números Naturais
A necessidade de contar objetos, animais, alimentos etc., é tão antiga quanto a própria humanidade. De tal necessidade, surgiu um conjunto numérico chamado: números naturais, representado pela letra ℕ. Tal conjunto pode ser representado da seguinte maneira:

Os três pontos “…” indicam que tal conjunto numérico é infinito, ou seja, não tem fim. Por mais que tentemos imaginar um número extraordinariamente grande, sempre existirá um número maior.
Existem alguns(mas) autores(as) que não consideram o número 0 (zero) como um elemento pertencente ao conjunto dos números naturais (ℕ). Para este caso específico, representamos o conjunto dos números naturais, sem o 0 (zero), da seguinte maneira (N*):

Neste material, trataremos apenas dos números pertencentes ao conjunto dos números naturais (ℕ).
2ª Etapa: Sistema numérico posicional
Lembremos:
- Um grupo de 10 (dez) unidades é chamado de dezena;
- Um grupo de 100 (cem) unidades é chamado de centena;
- Um grupo de 1 000 (mil) unidades é chamado de unidade de milhar;
- Um grupo de 10 000 (dez mil) unidades é chamado de dezena de milhar;
- Um grupo de 100 000 (cem mil) unidades é chamado de centena de milhar;
- Um grupo de 1 000 000 (um milhão) de unidades é chamado de unidade de milhão;
- Um grupo de 10 000 000 (dez milhões) de unidades é chamado de dezena de milhão;
- Um grupo de 100 000 000 (cem milhões) de unidades é chamado de centena de milhão;
- Um grupo de 1 000 000 000 (um bilhão) de unidades é chamado de unidade de bilhão;
- Etc.
Dessa forma, pode-se organizar os números em classes:
- Classe das unidades simples (1ª classe);
- Classe dos milhares (2ª classe);
- Classe dos milhões (3ª classe);
- Classe dos bilhões (4ª classe);
- Etc.
Partindo da classe das unidades simples, enumeramos, de forma crescente da direita para a esquerda, a ordem de grandeza. Todas essas informações podem ser sintetizadas no quadro a seguir:
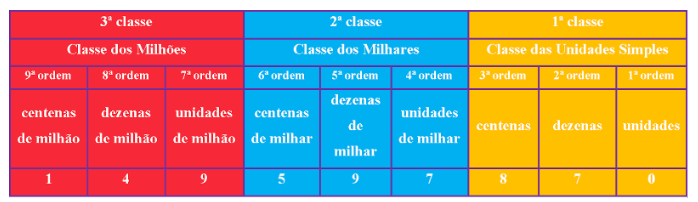
O nosso sistema numérico é posicional, ou seja, dependendo da posição ocupada por um certo algarismo em um número, ele terá um determinado valor.
No quadro anterior, na última linha, nós temos o número: 149 597 870 (cento e quarenta e nove milhões, quinhentos e noventa e sete mil, oitocentos e setenta).
Consideremos o algarismo 9 (nove). Ele aparece duas vezes no número que acabamos de efetuar a leitura. Partindo da direita para a esquerda, tem-se que o primeiro algarismo 9 (nove) ocupa a casa das dezenas de milhar, logo, ele representa 90 000 (noventa mil) unidades. No entanto, o segundo algarismo 9 (nove) ocupa a casa das unidades de milhão, portanto, ele representa 9 000 000 (nove milhões) unidades.
Para uma melhor compreensão do que acabou de ser apresentado, vejamos o seguinte exemplo:
- Consideremos as posições ocupadas pelo algarismo 8 (oito) nos seguintes números:
- 98 -> noventa e oito;
- 84 -> oitenta e quatro;
- 822 -> oitocentos e vinte e dois.
- No primeiro caso (I), o algarismo 8 (oito) representa oito unidades, pois ele está na posição da casa das unidades (1ª ordem);
- Já no segundo caso (II), o algarismo 8 (oito) representa oito dezenas (ou oitenta unidades), pois ele está na posição da casa das dezenas (2ª ordem);
- E no terceiro caso (III), o algarismo 8 (oito) representa oito centenas (ou oitocentas unidades), pois ele está na posição da casa das centenas (3ª ordem).
Assim, a quantidade numérica que um determinado algarismo representa sempre dependerá da posição que tal algarismo ocupa em um certo número.
3ª Etapa: Decomposição de números naturais
O conjunto dos números naturais (ℕ) surgiu da necessidade de efetuar contas, de quantificar as coisas.
Com o intuito de facilitar algumas contas, principalmente aquelas para as quais não podemos utilizar uma calculadora, serve-nos o conhecimento do seguinte procedimento matemático: decomposição de números naturais.
Um número composto por dois algarismos é um número que pertence à classe das unidades simples (1ª classe). Logo, tal número terá um algarismo que representará a quantidade de unidades que ele possui, e um outro algarismo que representará a quantidade de dezenas que o ele possui.
Dessa forma, a decomposição de um número natural (ℕ) formado por dois algarismos nada mais é do que identificar a quantidade de unidades que ele possui, a quantidade de dezenas que ele possui (transformá-las em unidades), e reescrevê-lo como uma soma. Vejamos:
Exemplo 1: Decomponha os seguintes números:
- 19 = 1 (dezena) + 9 (unidades) = 10 + 9
- 25 = 2 (dezenas) + 5 (unidades) = 20 + 5
- 43 = 4 (dezenas) + 3 (unidades) = 40 + 3
- 55 = 5 (dezenas) + 5 (unidades) = 50 + 5
- 68 = 6 (dezenas) + 8 (unidades) = 60 + 8
Agora, consideremos um número formado por três algarismos. Tal número também pertence à classe das unidades simples (1ª classe). Logo, ele terá um algarismo que representará a quantidade de centenas, um outro algarismo que representará a quantidade de dezenas, e outro algarismo que representará a quantidade de unidades. Vejamos como decompor números naturais compostos por três algarismos:
Exemplo 2: Decomponha os seguintes números:
- 822 = 8 (centenas) + 2 (dezenas) + 2 (unidades) = 800 + 20 + 2
- 650 = 6 (centenas) + 5 (dezenas) + 0 (unidades) = 600 + 50
- 727 = 7 (centenas) + 2 (dezenas) + 7 (unidades) = 700 + 20 + 7
- 987 = 9 (centenas) + 8 (dezenas) + 7 (unidades) = 900 + 80 + 7
O procedimento é o mesmo para números formados por quatro, cinco, seis, …, algarismos.
Exemplo 3: Decomponha os seguintes números naturais:
- 2 023 = 2 (unidades de milhar) + 0 (centenas) + 2 (dezenas) + 3 (unidades) = 2 000 + 20 + 3
- 16 436 = 1 (dezena de milhar) + 6 (unidades de milhar) + 4 (centenas) + 3 (dezenas) + 6 (unidades) = 10 000 + 6 000 + 400 + 30 + 6
- 384 042 = 3 (centenas de milhar) + 8 (dezenas de milhar) + 4 (unidades de milhar) + 0 (centenas) + 4 (dezenas) + 2 (unidades) = 300 000 + 80 000 + 4 000 + 40 + 2
Materiais Relacionados
Para ler conteúdos sobre decomposição de números:
- Decomposição de números no sistema de numeração decimal – Toda Matéria.
Acesso em: 12 de janeiro de 2023. - Composição e Decomposição de números naturais – ischoolmaputo1.
Acesso em: 12 de janeiro de 2023.
Para ver vídeos sobre decomposição de números:
- Decomposição de Números Naturais – Gis com Giz Matemática
Acesso em: 12 de janeiro de 2023. - Decomposição de Números Naturais – Dicasdemat Sandro Curió
Acesso em: 12 de janeiro de 2023.

