Conteúdos

Este roteiro de estudos de matemática apresenta o que é um sistema linear, além de trazer alguns métodos de resolução para tal tipo de sistema.

Após indicação de leitura, questões sobre o material sugerido são feitas, visando auxiliar na fixação do conteúdo.

O material também conta com sugestões de vídeos (possibilitando a ampliação e o aprofundamento em determinados tópicos).

Na última etapa, há alguns exercícios resolvidos.

Objetivos

• Compreender o que é um sistema linear; e
• Conhecer alguns métodos de resolução de sistemas lineares.

Conteúdos / Objetos do conhecimento:

• Sistemas lineares;
• Resolução de sistemas lineares; e
• Checagem dos seus conhecimentos.

Palavras-chave:

Sistemas lineares. Tipos de sistemas lineares.

Proposta de trabalho:

O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente.

Nesse sentido, apresenta um percurso com textos-base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.

Não é necessário fazer todas as etapas, ler todos os textos, ou assistir a todos os vídeos, mas as questões norteadoras, bem como as subquestões que advêm delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.

Leia os textos propostos, sempre buscando as respostas para cada uma das perguntas.

Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aumentar ainda mais a pesquisa.

Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.

1ª Etapa: Sistemas lineares

Pergunta norteadora: O que são sistemas lineares?

OLIVEIRA, Raul Rodrigues de. “Sistemas lineares”; PreParaEnem.

Acesso em: 22 de agosto de 2023.

              A partir do texto acima, responda às seguintes perguntas:

1. O que é um sistema linear?
2. O que define uma equação linear?
3. Quantos tipos de sistemas lineares existem? Quais são eles?
4. Quantas soluções possui um sistema linear do tipo Sistema Possível Determinado?
5. Quantas soluções possui um sistema linear do tipo Sistema Possível Indeterminado?
6. Quantas soluções possui um sistema linear do tipo Sistema Impossível?

Para saber mais, assista:

Sistemas – Conceitos básicos (Equação Linear) – Equaciona Com Paulo Pereira.

              Acesso em 22 de agosto de 2023.

Respostas da 1ª Etapa

1. Sistema linear é um conjunto de equações lineares. As equações de tal conjunto estão relacionadas entre si, o que significa dizer que elas possuem as mesmas variáveis e as mesmas soluções.
2. Uma equação é linear quando as suas variáveis possuem grau 1.
3. Existem três tipos de sistemas lineares. São eles: Sistema Possível Determinado; Sistema Possível Indeterminado; Sistema Impossível.
4. Um sistema linear classificado como Sistema Possível Determinado possui uma única solução.
5. Um sistema linear classificado como Sistema Possível Indeterminado possui infinitas soluções.
6. Um sistema linear classificado como Sistema Impossível não possui solução.

2ª Etapa: Resolução de sistemas lineares

Pergunta norteadora: Como resolver sistemas lineares?

OLIVEIRA, Raul Rodrigues de. “Sistemas lineares”; Brasil Escola.

Acesso em 22 de agosto de 2023.

              A partir do texto acima, responda às seguintes perguntas:

1. Quais métodos podem ser utilizados para resolver sistemas lineares que possuem duas equações e duas incógnitas?
2. Quando um sistema possui três equações lineares e três incógnitas, quais métodos de resolução devem ser utilizados?

Para saber mais, assista:

Sistemas 2×2– Resolução (Substituição, Adição e Comparação) – Equaciona Com Paulo Pereira.

Acesso em: 22 de agosto de 2023.

Escalonamento (Sistemas 3×3) – Equaciona Com Paulo Pereira.

              Acesso em: 22 de agosto de 2023.

Regra de Cramer (Sistemas 3×3) – Equaciona Com Paulo Pereira.

Acesso em 22 de agosto de 2023.

Respostas da 2ª Etapa

1. Existem vários métodos para resolver sistema lineares que possuem duas equações e duas incógnitas. Os mais conhecidos são:

• Método da substituição;
• Método da comparação; e
• Método da adição.

     2. Os métodos mais utilizados para a resolução de sistemas lineares com três equações e três incógnitas são: Regra de Cramer e o Escalonamento.

3ª Etapa: Cheque seus conhecimentos

Realizar questões de vestibular e do Enem é um excelente exercício durante o estudo autodirigido. A justificativa é porque essas questões são seguidas de gabarito, mesmo quando são dissertativas.

Seguem abaixo alguns exemplos de questões sobre o tema estudado:

1. Durante uma visita à padaria, Kárita comprou 2 pedaços de bolo de cenoura e uma dose de café, pagando, ao todo, R$ 3,50. Sua irmã, Karla, comprou 1 pedaço de bolo de cenoura e 2 doses de café, pagando um total de R$ 2,50. Analisando essa situação, se uma pessoa comprar 1 pedaço de bolo de cenoura e 1 café, o valor pago por ela será de:
   
   a) R$ 1,00
   b) R$ 1,50
   c) R$ 1,75
   d) R$ 2,00
   e) R$ 2,25

Resposta: Letra D.

Resolução:

Para montar o sistema de equações lineares, temos:

x  valor do pedaço do bolo de cenoura

y    valor da dose de café

Então, calcula-se:

Pelo método da substituição, isolando y na equação I, obtém-se o seguinte:

Substituindo y na equação II:

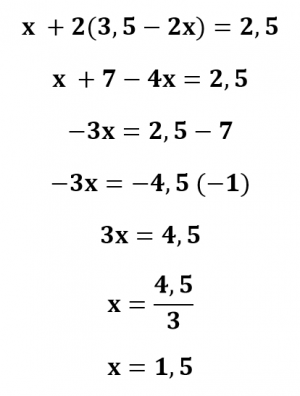
Sabendo que x = 1,5, substituímos o valor na equação I:

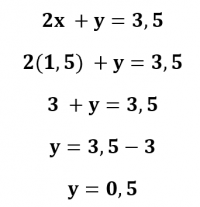
Sendo assim, o preço de um pedaço de bolo mais uma dose de café é de 1,5 + 0,5 = 2, ou seja, R$ 2,00. Portanto, a resposta correta é a letra D.

Exercícios – Brasil Escola.

Acesso em: 22 de agosto de 2023.

Em um estacionamento, há motos e carros, em um total de 25 veículos. Sabendo que há 74 rodas nesse estacionamento, podemos afirmar que

a) há 1 carro a mais que a quantidade de motos.
b) há 2 carros a mais que a quantidade de motos.
c) há 1 moto a mais que a quantidade de carros.
d) há 2 motos a mais que a quantidade de carros.

Resposta: Letra C.

Resolução:

Para montar o sistema de equações lineares, temos:

x → quantidade de carros

y → quantidade de motos

Então, calcula-se:

Isolando y na equação I, temos: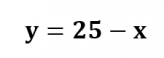
Substituindo y na equação II, temos:

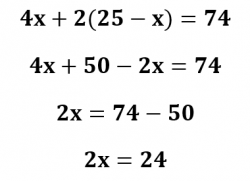
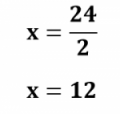
Portanto, há 12 carros.

Como há um total de 25 veículos, então 25 – 12 = 13. Logo, há 13 motos.

Podemos afirmar, portanto, que há 1 moto a mais que a quantidade de carros.

Assim, a resposta correta é a letra C.

Exercícios – Brasil Escola

Acesso em: 22 de agosto de 2023.

Roteiro de estudos elaborado pelo prof. me. Elves Silva Moreira.

Revisão textual: professora Daniela Leite Nunes.

Coordenação Pedagógica: prof. dr.ª Aline Bitencourt Monge.