Conteúdos
Neste roteiro de estudos, você irá estudar sobre as posições relativas entre duas retas, envolvendo análise algébrica e geométrica. O material traz ferramentas importantes para resolver problemas práticos em diversas áreas, como física, engenharia e computação.
Objetivos
- Identificar a posição relativa entre duas retas e sua relação com o coeficiente angular.
Conteúdos / Objetos do conhecimento:
- Posição relativa entre duas retas
Palavras-chave:
Retas. Posição relativa entre retas.
Proposta de trabalho:
A proposta é desenvolvida para que você, estudante, possa realizar os estudos em qualquer ambiente. Você estudará, primeiramente, sobre as posições relativas entre duas retas e, em seguida, sua relação com o coeficiente angular.
1ª Etapa: Posição relativa entre retas e sua relação com o coeficiente angular
Dentro da geometria analítica, podemos analisar a posição relativa entre duas retas, observando apenas a sua relação com os coeficientes angulares. Observe:
1° Caso: duas retas são paralelas.
Quando duas retas são ditas paralelas, isso implica em não terem pontos em comum; sendo assim, as suas inclinações são iguais.
Observe o exemplo com as seguintes equações:
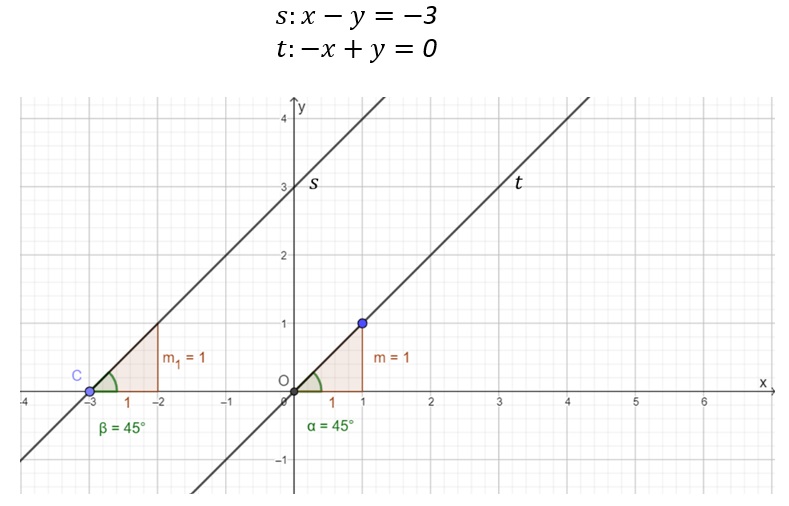
Os coeficientes angulares das duas retas são iguais, portanto elas são paralelas. Assim, sejam duas retas ![]()
2° Caso: duas retas concorrentes.
Quando duas retas são ditas concorrentes, indica que as duas retas possuem um único ponto em comum e seus coeficientes angulares são diferentes.
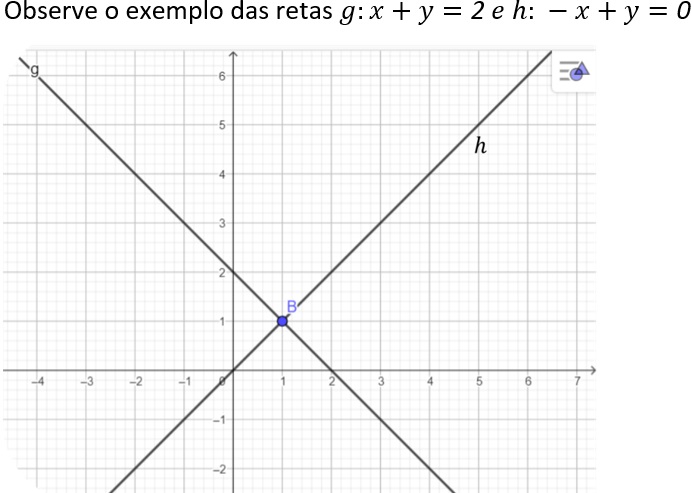
As duas retas possuem o ponto B(1,1) em comum.
3° Caso: Retas concorrentes e perpendiculares.
Quando duas retas são ditas concorrentes e perpendiculares, indica que as duas retas possuem um único ponto em comum e formam um ângulo de 90° entre si. Observe:
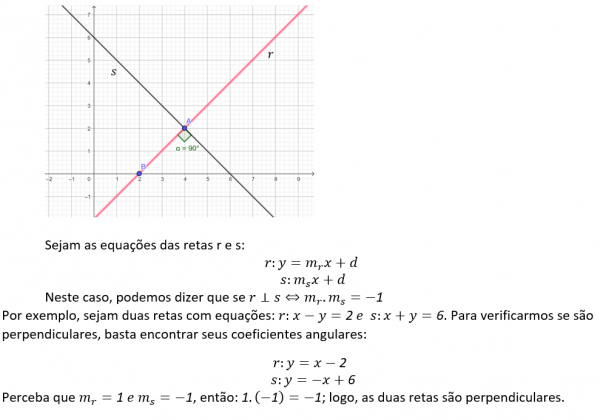
Agora é sua vez: tente resolver os seguintes exercícios:
- Qual é a equação reduzida da reta r, que é perpendicular à reta t:y=x+2 e passa pelo ponto (1,2)?
- Determine a equação geral da reta t, paralela à equação r:2x+y=2 e que passa pelo ponto (5,2).
- Qual é o coeficiente angular da reta perpendicular à reta r:5x+2y=3?

2ª Etapa: Praticando
1) (UFAM) Considere as retas r: 2y − x =10 e s: y + 2x = 5. É correto afirmar que:
a) As retas são paralelas.
b) As retas são perpendiculares.
c) As retas são concorrentes no ponto (5,0).
d) As retas são concorrentes no ponto (-10,0).
e) As retas são coincidentes.
Gabarito:
Primeiro, encontraremos o coeficiente angular da reta r:
Em seguida, encontramos o coeficiente angular da reta s:
Como o coeficiente angular da primeira reta é o inverso do oposto do coeficiente angular da segunda reta, as duas retas são perpendiculares.
Crédito: Projeto Agatha Questões
2) (URCA) Considerando as retas r: x – y + 1 = 0; s: 2x – y + 4 = 0 e t: x = -3, é correto afirmar que:
a) As retas r e s são paralelas.
b) As retas r e t são perpendiculares.
c) As retas r, s e t se intersectam num único ponto.
d) A reta s intersecta a circunferência de centro (0,0) e raio 1.
e) Nenhuma das anteriores.
Gabarito:
Primeiro, encontraremos o coeficiente angular da reta r:
Em seguida, encontramos o coeficiente angular da reta s:
Por fim, encontramos o coeficiente angular da reta t:
Observe que os coeficientes angulares são diferentes, portanto, se encontram em um único ponto.
Crédito: Projeto Agatha Edu
3) Determine a equação da reta que passa pelo ponto A (2, 1) e que possui uma inclinação de 45°.
Questão adaptada pelo autor.
Materiais Relacionados
Para te ajudar a complementar os estudos, você pode acessar:
“G. A. POSIÇÃO RELATIVA DE RETAS – Paralelismo e Perpendicularismo”
Acesso em: 24 de janeiro de 2024.
Roteiro de estudos elaborado pelo professor Cícero Inacio dos Santos.
Revisão textual: professora Daniela Leite Nunes.
Coordenação Pedagógica: prof. dr.ª Aline Bitencourt Monge.




