Conteúdos

Este roteiro de estudos de matemática traz a definição do que é o sinal de uma função, fornecendo exemplos e explicações sobre como descobrir os sinais de uma função. Após indicação de leitura, algumas questões baseadas no texto são feitas para ajudar na fixação do conteúdo. O material também conta com uma sugestão de vídeo, possibilitando um maior aprofundamento do tema.  Na última etapa, há exercícios resolvidos.

Objetivos

• Compreender o que é uma função;
• Definir o que é sinal de uma função; e
• Resolver problemas que envolvam descobrir os sinais de uma função.

Conteúdos / Objetos do conhecimento:

• Estudo dos sinais de uma função.

Palavras-chave:

Funções. Sinais de uma função. Função do 1° grau. Função do 2° grau.

Proposta de trabalho:

O objetivo deste roteiro de estudos é apoiar os alunos na compreensão do que são funções e estudar os seus sinais.

Explore os materiais fornecidos como base, atentando-se para as respostas a cada pergunta orientadora. Durante a leitura, tome nota de quaisquer dúvidas que venham a surgir, aproveitando para praticar as questões em seu caderno. Após os estudos, escreva um breve resumo sintetizando os principais conceitos aprendidos e resolva as questões propostas.

1ª Etapa: Introdução às funções

Pergunta orientadora: O que é uma função?

Leia o texto disponível em: https://proenem.com.br/enem/matematica/teoria-de-funcoes/
Acesso em: 26 de junho 2024.

A partir da leitura do texto, responda às seguintes perguntas:

1) Qual a definição de uma função?

2) Como representamos uma função?

3) Como criar o gráfico de uma função?

Para saber mais, assista: Introdução às funções.
Disponível em: https://youtu.be/UhCpfopmjGQ
Acesso em: 26 de junho de 2024.

Respostas da 1ª etapa

1) Função é uma associação dos elementos de dois conjuntos, ou seja, a função indica como os elementos estão relacionados. Por exemplo, uma função de A em B significa associar cada elemento pertencente ao conjunto A a um único elemento que compõe o conjunto B, de forma que um valor de A não pode estar ligado a dois valores de B.

2) Em uma função f: A → B o conjunto A é chamado de domínio (D) e o conjunto B recebe o nome de contradomínio (CD). Um elemento de B, relacionado a um elemento de A, recebe o nome de imagem pela função. Agrupando todas as imagens de B, temos um conjunto imagem, que é um subconjunto do contradomínio.

Exemplo: observe os conjuntos A = {1, 2, 3, 4} e B = {1, 2, 3, 4, 5, 6, 7, 8}, sendo que a função que determina a relação entre os elementos f: A → B é x → 2x. Sendo assim, f(x) = 2x e cada x do conjunto A é transformado em 2x no conjunto B.

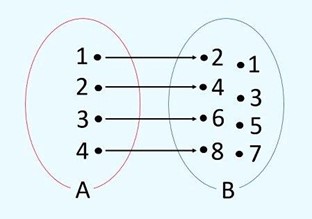
Note que os elementos do conjunto A {1, 2, 3, 4} são as entradas, “multiplicar por 2” é a função e os valores de B {2, 4, 6, 8}, que se ligam aos elementos de A, são os valores de saída.

Portanto, para essa função:

• O domínio é {1, 2, 3, 4}
• O contradomínio é {1, 2, 3, 4, 5, 6, 7, 8}
• O conjunto imagem é {2, 4, 6, 8}

3) A maneira como um elemento y se relaciona com um elemento x é expressa por meio de um gráfico, que nos dá a ideia do comportamento da função. Cada ponto no gráfico é dado por um par ordenado de x e y, onde x é o valor de entrada e y é o resultado da relação definida pela função.

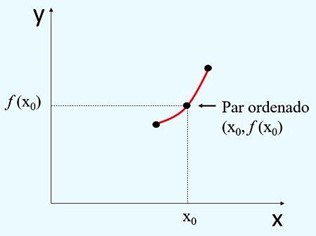
Para construir um gráfico, cada elemento x da função deve ser inserido no eixo horizontal (abscissas), e os elementos y são posicionados no eixo vertical (ordenadas). Os possíveis valores de x formam o conjunto domínio. Já o conjunto dos valores assumidos por y formam o conjunto imagem.

Confira alguns exemplos de gráficos de funções:

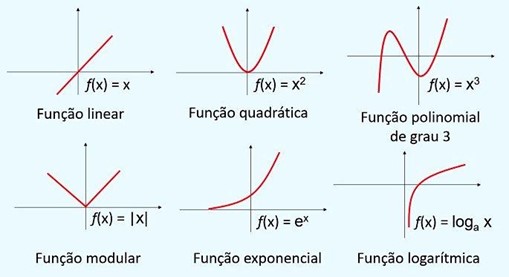
2ª Etapa: Estudo do sinal de uma função

Pergunta orientadora: Como determinar o sinal de uma função do 1º grau?

Leia o texto disponível em: Sinal da função do 1º grau
Disponível em: https://www.somatematica.com.br/emedio/funcao1/funcao1_3.php
Acesso em: 26 de junho de 2024.

A partir da leitura do texto acima, responda às seguintes perguntas:

1) O que significa estudar o sinal de uma função?

2) Qual é a raiz de uma função do 1º grau?

3) Como determinar o sinal de uma função crescente e decrescente?

Respostas da 2ª etapa

1) Estudar o sinal de qualquer função y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x para os quais y é zero e os valores de x para os quais y é negativo.

2) A raiz da função do 1º grau é encontrada quando y = 0. Para isso, lembramos que a função geral do 1º grau é y = ax + b. Sendo y = 0, temos:

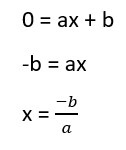
Portanto, para encontrar o valor de x em que a função se separa entre positivo e negativo, utilizamos a fórmula mostrada acima.

3) Há dois casos possíveis:

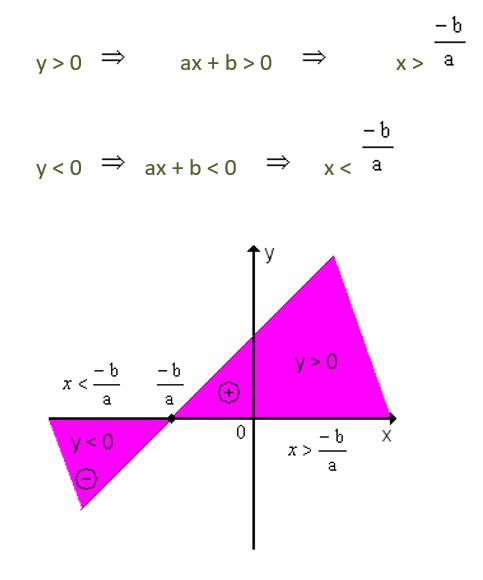
Quando a > 0, a função é crescente, portanto, y é positivo para valores de x maiores que a raiz e y é negativo para valores de x menores que a raiz.

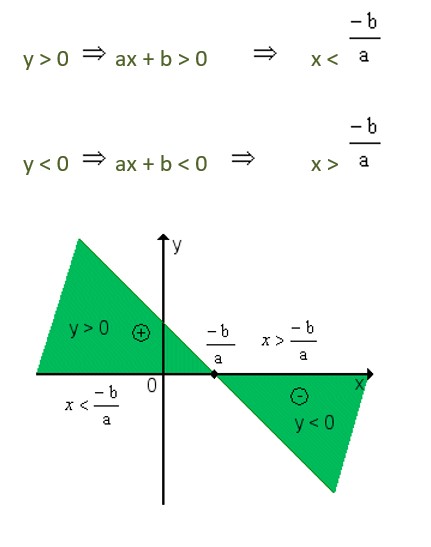
Quando a < 0, a função é decrescente, portanto, y é positivo para valores de x menores que a raiz e y é  negativo para valores de x maiores que a raiz.

3ª Etapa: Cheque seus conhecimentos

Resolver questões é extremamente importante para fixar um assunto, especialmente quando estudamos matemática. Abaixo, seguem alguns exemplos de questões sobre o tema estudado:

1) Determine os zeros das funções a seguir:

a) y = 5x + 2

b) y = – 2x

2) Classifique cada uma das funções seguintes em crescente ou decrescente:

a) y = 4x + 6

b) f(x) = – x + 10 

3) Determine o zero da função f(x) = -2x + 5.

Respostas da 3ª etapa

1)

a) y = 5x + 2

b) y = – 2x

Façamos y = 0, então:

– 2x = 0, o número – 2 mudará de lado e realizará uma divisão. Mas, como o número zero dividido por qualquer número resulta em zero, x = 0.

O zero da função y = – 2x é x = 0.

2) Em uma função do tipo y = ax + b, o coeficiente a de x indica se a função é crescente ou decrescente.

a) y = 4x + 6

Nessa função, a = 4 > 0, portanto y é uma função crescente.

b) f(x) = – x + 10

Como a = – 1 < 0, f(x) é uma função decrescente.

3) Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então temos que:

-2x + 5 = 0

-2x = -5

x = (-5) : (-2)

x = 2,5

Exercícios disponíveis em:

• Exercícios sobre Função do 1º Grau
  Acesso em: 26 de junho de 2024.
• Exercícios sobre função do 1º grau
  Acesso em: 26 de junho de 2024.

Roteiro de estudos elaborado pela Professora Gabriela Ribeiro do Prado.

Revisão textual: Professora Daniela Leite Nunes.

Coordenação Pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.

Crédito da imagem: Marilyn Nieves – Getty Images