Conteúdos
Conteúdos:
● O que é um Movimento Circular Uniforme (MCU);
● Relação entre a força centrípeta e o MCU;
● Período e Frequência no MCU;
● Velocidade angular.
Objetivos
Competências/Objetivos de Aprendizagem:
● Compreender o que é um Movimento Circular Uniforme (MCU);
● Compreender que todo MCU tem aceleração centrípeta;
● Entender que todo MCU é um movimento periódico.
Palavras-Chave:
Movimento Circular Uniforme. Força centrípeta. Aceleração centrípeta. Período. Frequência. Velocidade angular.
Proposta de Trabalho:
O objetivo deste roteiro é auxiliar nos estudos em casa ou em outro ambiente. Nesse sentido, apresenta um percurso com textos base e algumas propostas de atividades, e, no final, há outros textos e vídeos que podem ajudar a compreender melhor o tema em questão.
Não é necessário fazer todas as etapas, ler todos os textos, ou assistir todos os vídeos, mas as questões norteadoras, bem como as subquestões que advém delas, ajudam na captação do conteúdo inteiro e dos principais conceitos.
Leia os textos propostos buscando as respostas para cada uma das perguntas. Se aparecerem mais dúvidas ao longo da leitura, aproveite para fazer anotações em seu caderno e aprofundar sua pesquisa. Após as leituras de cada um dos textos, escreva um parágrafo resumindo seu aprendizado.
1ª Etapa: O que é um Movimento Circular Uniforme (MCU)?
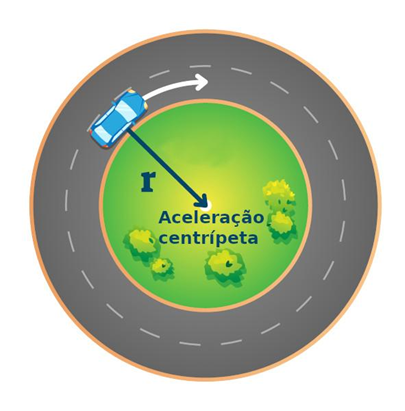
Pergunta norteadora:
Como podemos identificar um Movimento Circular Uniforme (MCU)?
Movimento circular uniforme (MCU) – Brasil Escola.
HELERBROCK, Rafael. “Movimento circular uniforme (MCU)”; Brasil Escola. Acesso em: 09 de outubro de 2020.
A partir da leitura do texto acima, responda às seguintes perguntas:
1) Elabore uma definição simples para o Movimento Circular Uniforme (MCU).
2) Qual é o tipo de trajetória que uma partícula descreve em um MCU?
3) O MCU é um movimento acelerado?
4) No MCU, a velocidade escalar varia ou é constante?
5) No MCU, a velocidade angular varia ou é constante?
Para saber mais, assista:
Física – MCU: Características do MCU – Pura Física.
2ª Etapa: Relação entre força centrípeta e MCU
Matematicamente, podemos escrever a força centrípeta como:
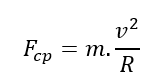 Onde:
Onde:

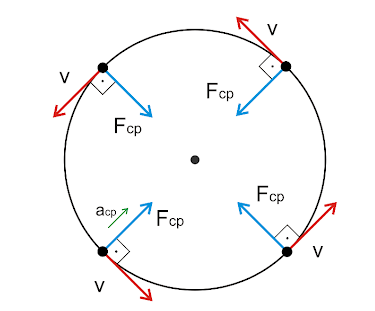
Pergunta norteadora:
Qual é a relação entre a força centrípeta e o MCU?
O que é força centrípeta – Brasil Escola – Joab Silas.
A partir da leitura do texto acima, responda às seguintes perguntas:
1) Elabore uma definição simples para a força centrípeta.
2) Qual é a grandeza física responsável pela mudança na direção e no sentido da velocidade no MCU?
3) Qual é o significado da palavra centrípeta?
4) Para qual direção aponta a aceleração centrípeta?
5) Qual é a força responsável por manter um corpo em uma trajetória circular?
6) Para qual direção aponta a força centrípeta?
7) O que é a “força centrífuga”? Ela realmente existe?
8) Qual é a relação da “força centrífuga” com a inércia?
Para saber mais, assista:
MCU: Aceleração e força centrípeta – Pura Física.
3ª Etapa: Período (T) e Frequência (f) no MCU
Matematicamente, podemos escrever o período (T) e a frequência (f) como:
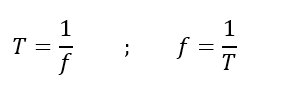
Pergunta norteadora:
Como podemos encontrar o Período (T) e a Frequência (f) de um Movimento Circular Uniforme (MCU)?
A partir da leitura do texto acima, responda às seguintes perguntas:
1) Como podemos definir a grandeza física período (T)?
2) No Sistema Internacional de Unidades (SI), qual é a unidade de medida para período (T)?
3) Como podemos definir a grandeza física frequência (f)?
4) No SI, qual é a unidade de medida para frequência?
5) Num Movimento Circular Uniforme (MCU), o período (T) e a frequência (f) são grandezas físicas constantes ou elas variam?
Para saber mais, assista:
Física – MCU: Período e frequência – Pura Física
4ª Etapa: Velocidade angular média (ω_m)
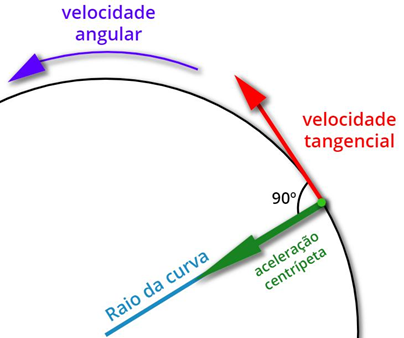
Matematicamente, podemos escrever a velocidade angular média (ω_m) como:
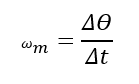
Onde:
ω_m=velocidade angular média[rad/s]
Δϴ=espaço angular [rad]
Δt=intervalo de tempo[s]
Pergunta norteadora:
Como podemos determinar a velocidade angular média (ω_m) num MCU?
Velocidade angular no MCU – PrePara Enem – Domiciano Correa Marques da Silva.
A partir da leitura do texto acima, responda às seguintes perguntas:
1)Por convenção, o sentido anti-horário para o deslocamento angular é positivo ou negativo?
2)Por convenção, o sentido horário para o deslocamento angular é positivo ou negativo?
3)Em graus, quanto vale 2π radianos?
4)Em radianos, quanto vale 360 º?
5) No SI, qual é a unidade de medida para velocidade angular média (ω_m)?
6) Matematicamente, como podemos relacionar a velocidade angular média (ω_m) com o período (T)?
7) Matematicamente, como podemos relacionar a velocidade angular média (ω_m) com a frequência (f)?
Para saber mais, assista:
MCU: Velocidade angular – Pura Física.
5ª Etapa: Cheque seus conhecimentos
Realizar questões de vestibular e do ENEM é um excelente exercício durante estudo autodirigido, isso porque essas questões são seguidas de gabarito, mesmo quando são dissertativas. Abaixo, alguns exemplos de questões sobre o tema estudado.
1) (Unifor) Um carrossel gira uniformemente, efetuando uma rotação completa a cada 4,0 segundos. Cada cavalo executa movimento circular uniforme com frequência em rps (rotação por segundo) igual a:
a) 8,0
b) 4,0
c) 2,0
d) 0,5
e) 0,25
Resposta: E
Justificativa:
A frequência (f) do movimento é dada em unidade de tempo de acordo com a divisão do número de voltas pelo tempo gasto para executá-las.
Para responder essa questão, basta substituir os dados do enunciado na fórmula a seguir:

Se uma volta é dada a cada 4 segundos, a frequência do movimento é de 0,25 rps.
Disponível em: Toda Matéria
Acesso em: 09 de outubro de 2020.
2) Um corpo em MCU consegue realizar 480 voltas no tempo de 120 segundos em torno de uma circunferência de raio 0,5 m. De acordo com essas informações, determine:
a) Frequência e período
Resolução:
A frequência (f) do movimento é dada em unidade de tempo de acordo com a divisão do número de voltas pelo tempo gasto para executá-las.

O período (T) representa o intervalo de tempo para que o movimento se repita. Período e frequência são grandezas inversamente proporcionais. A relação entre elas é estabelecida através da fórmula:
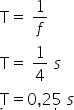
b) Velocidade angular e velocidade escalar
Resolução:
O primeiro passo para responder essa questão é calcular a velocidade angular do corpo.
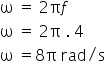
A velocidade escalar e angular são relacionadas a partir da fórmula a seguir.
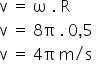
Disponível em: Toda Matéria Acesso em: 09 de outubro de 2020.
3) (UMC) Numa pista circular horizontal, de raio igual a 2 km, um automóvel se movimenta com velocidade escalar constante, cujo módulo é igual a 72 km/h. Determine o módulo da aceleração centrípeta do automóvel, em m/s2.
Resolução:
Como a questão pede a aceleração centrípeta em m/s2, o primeiro passo para resolvê-la é converter as unidades do raio e da velocidade escalar.
Se o raio é de 2 km e sabendo que 1 km possui 1000 metros, logo, 2 km correspondem a 2000 metros.
Para converter a velocidade escalar de km/h para m/s basta dividir o valor por 3,6.
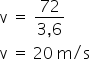
A fórmula para calcular a aceleração centrípeta é:
![]()
Substituindo os valores do enunciado na fórmula, encontramos a aceleração.
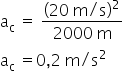
Disponível em Toda Matéria. Acesso em: 09 de outubro de 2020.
4) (UFPR) Um ponto em movimento circular uniforme descreve 15 voltas por segundo em uma circunferência de 8,0 cm de raio. A sua velocidade angular, o seu período e a sua velocidade linear são, respectivamente:
a) 20 rad/s; (1/15) s; 280 π cm/s
b) 30 rad/s; (1/10) s; 160 π cm/s
c) 30 π rad/s; (1/15) s; 240 π cm/s
d) 60 π rad/s; 15 s; 240 π cm/s
e) 40 π rad/s; 15 s; 200 π cm/s
Resposta: C
Resolução:
1º passo: Calcular a velocidade angular aplicando os dados na fórmula.
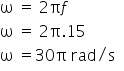
2º passo: Calcular o período aplicando os dados na fórmula.
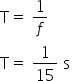
3º passo: Calcular a velocidade linear aplicando os dados na fórmula.

Disponível em Toda Matéria. Acesso em: 09 de outubro de 2020.
5) (UEM) Sobre o movimento circular uniforme, assinale o que for correto.
01. Período é o intervalo de tempo que um móvel gasta para efetuar uma volta completa.
02. A frequência de rotação é dada pelo número de voltas que um móvel efetua por unidade de tempo.
04. A distância que um móvel em movimento circular uniforme percorre ao efetuar uma volta completa é diretamente proporcional ao raio de sua trajetória.
08. Quando um móvel efetua um movimento circular uniforme, sobre ele atua uma força centrípeta, a qual é responsável pela mudança na direção da velocidade do móvel.
16. O módulo da aceleração centrípeta é diretamente proporcional ao raio de sua trajetória.
Respostas corretas: 01, 02, 04 e 08.
Justificativas:
01. CORRETA. Quando classificamos o movimento circular como periódico, significa que uma volta completa é dada sempre no mesmo intervalo de tempo. Por isso, período é o tempo que o móvel leva para efetuar uma volta completa.
02. CORRETA. A frequência relaciona o número de voltas com o tempo gasto para efetuá-las.

O resultado representa o número de voltas por unidade de tempo.
04. CORRETA. Ao efetuar uma volta completa no movimento circular, a distância percorrida por um móvel é a medida da circunferência.
![]()
Sendo assim, a distância é diretamente proporcional ao raio de sua trajetória.
08. CORRETA. No movimento circular, o corpo não realiza uma trajetória, pois uma força age sobre ele mudando a sua direção. A força centrípeta age direcionando-o para o centro.
![]()
A força centrípeta age na velocidade (v) do móvel.
16. ERRADA. As duas grandezas são inversamente proporcionais.
![]()
O módulo da aceleração centrípeta é inversamente proporcional ao raio de sua trajetória.
Disponível em Toda Matéria. Acesso em: 09 de outubro de 2020.
6) (UERJ) A distância média entre o Sol e a Terra é de cerca de 150 milhões de quilômetros. Assim, a velocidade média de translação da Terra em relação ao Sol é, aproximadamente, de:
a) 3 km/s
b) 30 km/s
c) 300 km/s
d) 3000 km/s
Resposta: B
Resolução:
Como a resposta deve ser dada em km/s, o primeiro passo para facilitar a resolução da questão é colocar a distância entre Sol e Terra em notação científica.
![]()
Como a trajetória é realizada ao redor do Sol, o movimento é circular e sua medida é dada pelo perímetro da circunferência.
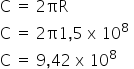
O movimento de translação corresponde à trajetória realizada pela Terra ao redor do Sol no período de aproximadamente 365 dias, ou seja, 1 ano.
Sabendo que um dia tem 86.400 segundos, calculamos quantos segundos têm em um ano multiplicando pelo número de dias.
![]()
Passando esse número para notação científica, temos:
![]()
A velocidade de translação é calculada da seguinte forma:
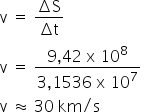
Disponível em Toda Matéria. Acesso em: 09 de outubro de 2020.
7) (UEMG) Em uma viagem a Júpiter, deseja-se construir uma nave espacial com uma seção rotacional para simular, por efeitos centrífugos, a gravidade. A seção terá um raio de 90 metros. Quantas rotações por minuto (RPM) deverá ter essa seção para simular a gravidade terrestre? (considere g = 10 m/s²).
a) 10/π
b) 2/π
c) 20/π
d) 15/π
Resposta: A
Resolução:
O cálculo da aceleração centrípeta é dado pela seguinte fórmula:
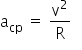
A fórmula que relaciona a velocidade linear com a velocidade angular é:
![]()
Substituindo essa relação na fórmula da aceleração centrípeta, temos:
![]()
A velocidade angular é dada por:
![]()
Transformando a fórmula da aceleração chegamos à relação:
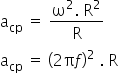
Substituindo os dados na fórmula, encontramos a frequência da seguinte forma:
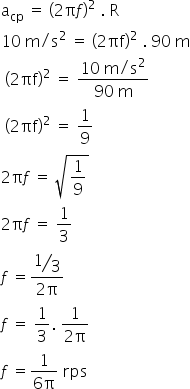
Esse resultado está em rps, que significa rotações por segundo. Através da regra de três encontramos o resultado em rotações por minuto, sabendo que 1 minuto tem 60 segundos.
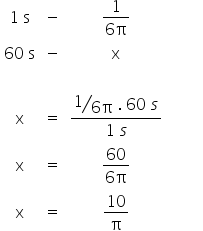
Disponível em Toda Matéria. Acesso em: 09 de outubro de 2020.
Roteiro de estudos elaborado pelo Professor Elves Silva Moreira




