Conteúdos

Este roteiro de estudos de matemática tem como objetivo definir o conceito de função e apresentar exemplos e explicações sobre domínio da imagem de uma função, bem como uma abordagem sobre o seu contradomínio. Após a indicação de leitura, algumas questões sobre o material sugerido são feitas, visando uma maior fixação do conteúdo. O material também conta com uma sugestão de vídeo, possibilitando um maior aprofundamento no tema. Na última etapa, há alguns exercícios resolvidos.

Objetivos

• Compreender o que é uma função;
• Definir o que é domínio de uma função; e
• Relacionar domínio e imagem de funções.

Conteúdos / Objetos do conhecimento:

• Domínio e imagem de uma função.

Palavras-chave:

Domínio e imagem de uma função. Domínio de funções. Imagem de funções. Contradomínio de funções.

Proposta de estudos:

O objetivo deste material é apoiar os alunos na compreensão do que são funções e como relacionar uma função ao seu domínio, ao seu contradomínio e a sua imagem.

Explore os materiais fornecidos como base, atentando-se para as respostas a cada pergunta orientadora. Durante a leitura, tome nota de quaisquer dúvidas adicionais que eventualmente surjam, aproveitando para praticar as questões em seu caderno. Após os estudos, escreva um breve resumo sintetizando os principais conceitos aprendidos e resolva as questões propostas.

1ª Etapa: Introdução às funções

Pergunta orientadora: O que é uma função?

Leia o texto disponível: Conceito de função, domínio e imagem
*acesso em: 24 de maio 2024

A partir da leitura do texto acima, responda às seguintes perguntas:

• Como definimos uma função?
• Por que é importante identificar o domínio de uma função antes de analisar seu comportamento ou representá-la graficamente?
• Como a noção de imagem de uma função está relacionada ao seu domínio?

Para saber mais, assista ao vídeo: Domínio, contradomínio e imagem da função
*acesso em: 25 de maio de  2024

Respostas da 1ª etapa

• Para definir uma função, necessitamos de dois conjuntos (domínio e contradomínio) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um, e somente um, elemento do contradomínio.
• Identificar o domínio de uma função é crucial porque nos informa sobre quais valores de entrada são válidos para a função. Assim, podemos evitar operações indefinidas e entender as restrições da função, observando o seu comportamento e representando graficamente com precisão.
• A imagem de uma função é o conjunto de todos os valores de saída que a função pode produzir para os valores de entrada em seu domínio. A relação entre imagem e domínio é que a imagem está diretamente ligada aos valores que a função pode produzir para os valores permitidos em seu domínio. Determinar a imagem de uma função, especialmente quando o domínio é contínuo e ilimitado, envolve analisar o comportamento da função e seus limites quando os valores de entrada se aproximam de extremos. Isso nos permite identificar os valores que a função pode atingir.

2ª Etapa: Domínio x imagem

Pergunta orientadora: Qual a diferença entre domínio e imagem?

Leia o texto disponível: Domínio e imagem de uma função
*acesso em: 24 de maio de  2024

A partir da leitura do texto acima, responda às seguintes perguntas:

• O que é contradomínio de uma função?
• O que é imagem de uma função?
• Como determinar o domínio de uma função matemática?

Respostas da 2ª Etapa

• O contradomínio de uma função é o conjunto de todos os valores de saída que a função pode gerar. É um conjunto predefinido de valores no qual as saídas da função estão contidas.
• O domínio de uma função é o conjunto de todos os valores de entrada da função para os quais ela está definida. Em outras palavras, é o conjunto de todos os valores que podem ser colocados na função para produzir uma saída.
• Para determinar o domínio de uma função, é necessário identificar todos os valores que podem ser utilizados como entrada sem causar indeterminações ou resultados inválidos. Exemplos: para funções racionais, excluir valores que tornam o denominador zero. Para funções de raiz quadrada, garantir que o radicando seja não negativo (no conjunto dos números reais).

3ª Etapa: Cheque seus conhecimentos

Resolver questões é extremamente importante para fixar um assunto quando estudamos matemática. Abaixo, seguem alguns exemplos de questões sobre o tema estudado:

1) Dada a função f(x) = 2x – 3, o domínio {2, 3, 4} e o contradomínio composto pelos naturais entre 1 e 10, qual das opções abaixo representa o conjunto imagem dessa função?

a) {1, 3, 5}

b) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

c) {4, 6, 8}

d) {1, 2, 3, 4, 5}

e) {1, 3, 8}

2) Descubra o conjunto que não pertence ao domínio da função a seguir:

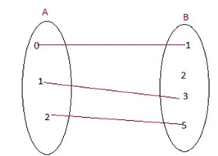
3) Analise o diagrama abaixo e determine: o domínio, o contradomínio e o conjunto imagem.

Respostas da 3ª Etapa

1) Para determinar os valores da imagem, será necessário aplicar cada valor do domínio na função.

f(x) = 2x – 3

f(2) = 2·2 – 3

f(2) = 4 – 3

f(2) = 1

Fazendo os cálculos, descobriremos: f(3) = 3 e f(4) = 5, portanto, os elementos do contradomínio que representam algum elemento do domínio são: 1, 3 e 5, portanto a imagem é: {1, 3, 5}.

2) Uma raiz somente é definida quando seu radicando não é negativo. Portanto, para que a função acima seja válida, os valores de x não podem ser tais que 4x – 16 seja menor que zero. Assim:

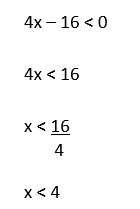
Qualquer valor de x inferior a 4 torna essa função inválida. Logo, o domínio dessa função não pode conter o número 2, que é menor que 4.

3) Pelo diagrama, temos:

Domínio: D (f) = {0, 1, 2}
Contradomínio: CD (f) = {1, 2, 3, 5}
Conjunto Imagem: Im (f) = {1, 3, 5}

Essa função é definida por: 2x +1

Observe que não há nenhum elemento x em A, que substituindo em 2x + 1 resulta em 2. Por conta disso, não há associação.

Exercícios disponíveis em:

Exercícios sobre domínio de funções

Exercícios sobre domínio, contradomínio e imagem

Roteiro de estudos elaborado pela Professora Gabriela Ribeiro do Prado.

Revisão textual: Professora Daniela Leite Nunes.

Coordenação Pedagógica: Prof.ª Dr.ª Aline Monge.

Crédito da imagem: JLGutierrez – Getty Images