Conteúdos
Fazendo uso de metodologias ativas, este plano de aula tem como objetivo explicar o que são frações equivalentes e qual a sua importância no estudo da matemática.
Objetivos
- Compreender o conceito de frações equivalentes;
- Identificar frações equivalentes por meio de simplificação e multiplicação de numeradores e denominadores;
- Resolver exercícios que envolvam a comparação e a simplificação de frações; e
- Aplicar o conceito de frações equivalentes em situações cotidianas.
Conteúdos/Objetos do conhecimento:
- Definição de frações equivalentes;
- Estratégias para encontrar frações equivalentes: multiplicação e divisão dos termos; e
- Como simplificar frações.
Palavras-chave:
Frações equivalentes. Frações.
Previsão para aplicação:
3 aulas (50 min/aula).
1ª Etapa: Retomando frações
Inicie a aula perguntando para a turma se sabe o que são frações e qual a sua utilidade no cotidiano (dividir alimentos, medir ingredientes etc.).
Após a retomada, aproveite para explicar o conceito de frações equivalentes. Fale aos alunos que as frações equivalentes são frações que representam a mesma parte de um todo, embora possuam numeradores e denominadores diferentes.
2ª Etapa: Exposição teórica
Apresente exemplos simples de frações equivalentes:
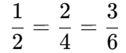
Explique como multiplicar o numerador e o denominador da fração por um mesmo número, para gerar frações equivalentes.
Para ajudar os alunos no entendimento, utilize figuras geométricas (círculos ou retângulos) divididas em partes iguais, ilustrando as frações.
Por meio da contextualização, apresente aos alunos uma situação simples, como a divisão de uma pizza ou de um bolo em partes iguais. Pergunte aos alunos se, ao cortar a pizza de forma diferente, ainda teremos a mesma quantidade para cada pessoa (frações equivalentes).
Peça aos alunos que pintem as frações equivalentes em diferentes formas e comparem os resultados.
Exemplo:
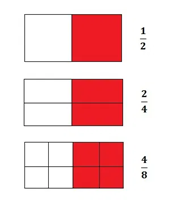
3ª Etapa: Resolução de exercícios
Partindo das descobertas ocorridas na etapa anterior, dê uma folha de exercícios com atividades para que os alunos tentem resolver. Faça o primeiro exercício como exemplo:
Exemplo: Encontre frações equivalentes a 1/3, multiplicando o numerador e o denominador por 2, 3 e 4.
Resposta do exemplo:
Multiplicando por 2:
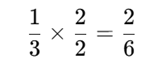
Multiplicando por 3:
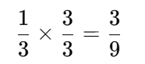
Multiplicando por 4:
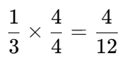
Frações equivalentes a 1/3;
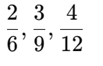
Exercícios:
1) Simplifique as frações 6/12, 15/45 e 8/24.
2) Complete o quadro de frações equivalentes:
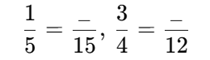
3) Encontre frações equivalentes de 1/3, multiplicando o numerador e o denominador por 2 e 3.
4) Simplifique a fração 4/8.
5) Complete a fração equivalente para 2/5, com denominador 25.
Gabarito:
1) Simplifique as frações:
6/12 = 1/2 (dividindo o numerador e o denominador por 6)
15/45 = 1/3 (dividindo por 15)
8/24 = 1/3 (dividindo por 8)
2) Complete o quadro de frações equivalentes:
1/5 = 3/15 (multiplicando por 3)
3/4 = 9/12 (multiplicando por 3)
3) Encontre frações equivalentes de 1/3:
Multiplicando por 2:
1/3 × 2/2 = 2/6
Multiplicando por 3:
1/3 × 3/3 = 3/9
4) Simplifique a fração 4/8:
4/8 = 1/2 (dividindo por 4)
5) Complete a fração equivalente para 2/5 com denominador 25:
Para obter denominador 25, multiplicamos por 5:
2/5 × 5/5 = 10/25
Perguntas para fazer aos alunos, como reflexão pós-aula:
- Como podemos saber se duas frações são equivalentes?
- Qual a diferença entre uma fração simplificada e uma fração equivalente?
- Como as frações equivalentes aparecem em situações do cotidiano?
Bom trabalho!
Plano de aula elaborado pela Professora Gabriela Ribeiro do Prado.
Coordenação Pedagógica: Prof.ª Dr.ª Aline Bitencourt Monge.
Revisão textual: Professora Daniela Leite Nunes.
Crédito da imagem: A-Digit – Getty Images

