Medidas de Volume

Publicado em 11 de novembro de 2022

2ª EtapaSubmúltiplos e múltiplos do metro cúbico

Conteúdos

Este plano de aula de Matemática apresenta, de forma introdutória, o conceito de “medidas de volume”. O material discute as dimensões das unidades de medida das grandezas: distância (comprimento), área e volume. Logo em seguida, os submúltiplos e os múltiplos da unidade de medida padrão do volume, o metro cúbico, são apresentados. Alguns exemplos resolvidos são discutidos na última etapa, visando a consolidação do conteúdo. O material também conta com algumas sugestões de textos e vídeos (em “Materiais relacionados”) para aprofundamento do(a) professor(a) sobre o assunto.

Objetivos

Compreender as dimensões das unidades de medidas das grandezas: distância, área e volume; e
Aprender a manipular as diversas formas de representação das unidades de medida de volume.

1ª Etapa: Introdução ao tema

Ao nos deslocarmos por uma determinada distância – por exemplo, a distância da nossa casa até a escola – podemos representar a medida do nosso trajeto de diferentes maneiras: em centímetros [cm], em metros [m], em quilômetros [Km], dentre outras. A distância (ou comprimento) é uma grandeza unidimensional (possui uma dimensão espacial), o que significa que a sua unidade de medida (cm, m, Km, etc.) tem expoente 1, ou seja:

Em Matemática, o objeto geométrico que possui uma única dimensão espacial é a reta. Portanto, ao medirmos uma determinada distância, podemos utilizar um segmento de reta que una um ponto inicial A a um ponto final B. Ao medirmos o tamanho (comprimento) do segmento de reta em questão, estaremos medindo a distância entre os pontos A e B.

Agora, suponhamos que alguém queira trocar os azulejos da cozinha de sua própria casa. Para comprar a quantidade adequada de azulejos, tal pessoa deverá estimar uma outra grandeza: a área da cozinha. Área é uma grandeza bidimensional, ou seja, possui duas dimensões espaciais. Logo, as suas unidades de medida possuem expoente 2. Assim, sempre que estivermos tratando da grandeza área, devemos representar as suas unidades de medida da seguinte maneira:

Em Matemática, o objeto geométrico que possui duas dimensões espaciais é o plano.

A mesma pessoa que está interessada em trocar os azulejos da cozinha, ficou empolgada e decidiu construir uma piscina no quintal de casa. Ela mediu a área do quintal e escolheu a profundidade da piscina. Nesse momento, ela precisa saber quantos litros de água serão necessários para encher a sua futura piscina. Tal pessoa está, de fato, empenhada em descobrir o volume (capacidade) da sua piscina. Naturalmente, o volume é uma grandeza tridimensional, ou seja, possui três dimensões espaciais. Por consequência, as unidades de medida de volume possuem expoente 3. Dessa forma, sempre que estivermos calculando o volume de um determinado objeto, devemos representar as suas unidades de medida da seguinte forma:

Em Matemática, o objeto geométrico que possui três dimensões é o espaço.

Neste material, estaremos concentrados nas diferentes formas de se representar a grandeza: volume, cuja unidade de medida padrão (ou seja, adotada pelo Sistema Internacional de Unidades (SI) é o metro cúbico [m³].

2ª Etapa: Submúltiplos e múltiplos do metro cúbico

Como já vimos na etapa anterior, a unidade de medida para a grandeza volume, adotada pelo SI, é o metro cúbico [m³].

Podemos admitir, como uma primeira definição para a grandeza volume, a seguinte sentença:

Volume: região do espaço ocupada por um determinado corpo.

Naturalmente, existem corpos com os mais diversos volumes, ou seja, com diferentes dimensões de largura, altura e profundidade. O produto das medidas dessas três dimensões é o volume de um certo corpo. Dessa forma, ao tratarmos de corpos com volumes muito pequenos, revela-se inconveniente representá-los com a unidade de medida padrão, o metro cúbico. Assim também acontece quando estamos tratando de corpos com volumes muito grandes. Para esses casos “extremos”, ou seja, quando estamos trabalhando com corpos com volumes diminutos, mostra-se conveniente expressar as suas unidades de medida com os submúltiplos do metro cúbico, e ao trabalharmos com corpos com volumes enormes, é conveniente expressar as suas unidades de medida com os múltiplos do metro cúbico.

Os principais submúltiplos do metro cúbico [m³] são:

Decímetro cúbico, cujo símbolo é → [dm³];
Centímetro cúbico, cujo símbolo é → [cm³];

Milímetro cúbico, cujo símbolo é → [mm³];

E os principais múltiplos do metro cúbico [m³] são:

Quilômetro cúbico, cujo símbolo é → [km³];
Hectômetro cúbico, cujo símbolo é → [hm³];
Decâmetro cúbico, cujo símbolo é → [dam³];

Podemos organizar todas essas informações em uma tabela, da seguinte forma:

Ao analisar a tabela anterior com cuidado, é possível observar que existe uma relação matemática entre todas as unidades de medida. Vejamos:

Para sair da unidade de medida padrão de volume (o metro cúbico [m³] ) para o decâmetro cúbico [dam³], dividimos o valor em metros cúbicos por 1 000 (mil). Dessa forma, tem-se que:

E, para fazer o caminho contrário, ou seja, transformar decâmetro cúbico [dam³] em metro cúbico [m³] , devemos multiplicar o valor em por 1 000 (mil):

Para transformar o metro cúbico [m³] em hectômetro cúbico [hm³], precisamos dividir o valor em por 1 000 000 (um milhão), ou seja, mil vezes mil. Assim:

Para fazer o caminho contrário, ou seja, transformar hectômetro cúbico [hm³] em metro cúbico [m³] , devemos multiplicar o valor em por 1 000 000 (um milhão):

Agora, o procedimento para transformarmos metro cúbico [m³] em quilômetro cúbico [km³], devemos dividir o valor em por 1 000 000 000 (um bilhão!), ou seja, mil vezes mil vezes mil. Assim:

E, para fazer o caminho contrário, ou seja, transformar quilômetro cúbico [km³] em metro cúbico [m³], devemos multiplicar o valor em por 1 000 000 000 (um bilhão):

Acabamos de tratar das formas como os múltiplos do metro cúbico se relacionam matematicamente.

Vejamos, agora, como os submúltiplos do metro cúbico se relacionam:

Para sairmos da unidade de medida padrão de volume (o metro cúbico [m³]) para o decímetro cúbico [dm³] , multiplicamos o valor em metros cúbicos por 1 000 (mil). Portanto:

E para fazer o caminho contrário, ou seja, transformar decímetro cúbico [dm³] em metro cúbico [m³] , devemos dividir o valor em por 1 000 (mil):

Para transformar o metro cúbico [m³] em centímetro cúbico [cm³], precisamos multiplicar o valor em por 1 000 000 (um milhão), ou seja, mil vezes mil. Assim:

Para fazer o caminho contrário, ou seja, transformar centímetro cúbico [cm³] em metro cúbico [m³] , devemos dividir o valor em por 1 000 000 (um milhão):

Finalmente, para transformar metro cúbico [m³] em milímetro cúbico [mm³], deve-se multiplicar o valor em por 1 000 000 000 (um bilhão!), ou seja, mil vezes mil vezes mil. Logo:

E, para fazer o caminho contrário, ou seja, transformar milímetro cúbico [mm³] em metro cúbico [m³] , devemos dividir o valor em por 1 000 000 000 (um bilhão), como segue:

Todas essas transformações de unidades de medida de volume, relacionando o metro cúbico com os seus múltiplos e submúltiplos, podem ser sintetizadas no seguinte esquema:

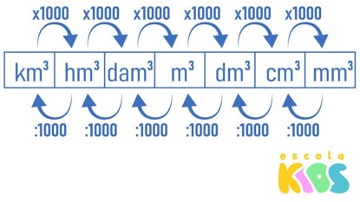
Figura disponível em: https://escolakids.uol.com.br/matematica/medidas-de-volume.htm.

Acesso em: 29 de setembro de 2022.

Ou seja, sempre que estivermos interessados em transformar uma determinada unidade de medida de volume em uma unidade de medida imediatamente à sua direita (ou seja, “caminhando” para a direita), devemos multiplicá-la por 1 000 (mil). E sempre que estivermos interessados em transformar uma determinada unidade de medida em uma unidade de medida de volume imediatamente à sua esquerda (ou seja, “caminhando” para a esquerda), devemos dividi-la por 1 000 (mil).

3ª Etapa: Exemplos resolvidos

Neste momento, veremos alguns exemplos resolvidos, para aplicar o que foi discutido, buscando consolidar os conceitos trabalhados.

Exemplo 1: O Cubo de Rubik, popularmente conhecido como cubo mágico (imagem), é um quebra-cabeça tridimensional, criado em 1974 por um professor de arquitetura, o húngaro Ernő Rubik. Consideremos o cubo mágico padrão, que possui 3 unidades em cada uma de suas arestas. Quantas unidades (peças), ou seja, quantos minicubos “idênticos”* formam um cubo mágico padrão?

Figura disponível em: https://pt.wikipedia.org/wiki/Cubo_de_Rubik.

Acesso em: 29 de setembro de 2022.

Resolução:

De fato, o que a questão nos pede é o volume do cubo mágico, em termos de uma determinada unidade: minicubo.

Sabemos que um cubo é um objeto geométrico que possui a característica de ter todas as suas dimensões iguais, ou seja, um cubo que possui 3 unidades (minicubos) de aresta, tem 3 unidades de largura, 3 unidades de altura e 3 unidades de profundidade. Assim, para calcularmos o volume do cubo mágico, basta multiplicarmos as medidas das suas três dimensões:

De uma maneira geral, chamamos a aresta de um cubo qualquer de a. Assim, o volume de todo e qualquer cubo é dado pela seguinte expressão:

*Observação 1: Os minicubos não são exatamente idênticos devido ao mecanismo interno responsável pela movimentação dos eixos do cubo mágico.

**Observação 2: Na prática, se desmontarmos um cubo mágico padrão (3x3x3), constataremos que ele é formado por 26 minicubos (peças). O volume que deveria ser do vigésimo sétimo minicubo (a 27ª peça) é ocupado pelo mecanismo que permite a movimentação de todos os seus eixos (faces).

Exemplo 2: Um balde possui um volume de 2 400 dm³ (decímetro cúbico). Qual é o volume desse balde em metro cúbico ?

Como vimos na etapa anterior, para transformarmos decímetro cúbico em metro cúbico [m³ ] devemos dividir o valor em por 1 000 (mil). Assim, temos:

Exemplo 3: Uma piscina possui um volume de 169 metros cúbicos (m³) de água. Qual é o seu volume, ou melhor, qual é a sua capacidade, em litros [l]?

Resolução:

Para resolver esta questão, é preciso relembrar a seguinte relação:

Ou seja, um metro cúbico é igual a mil litros. Assim, para transformarmos o valor em metros cúbicos para litros, devemos multiplicar o valor em [m³] por mil:

Observação: Outra relação importante é a seguinte:

Ou seja, um decímetro cúbico é igual a um litro.

Plano de aula elaborado pelo Prof. Me. Elves Silva Moreira.

Revisão textual: Professora Daniela Leite Nunes.

Coordenação Pedagógica: Professora Dr.ª Aline Bitencourt Monge